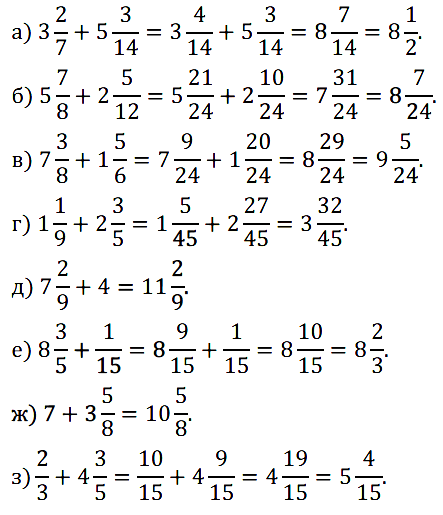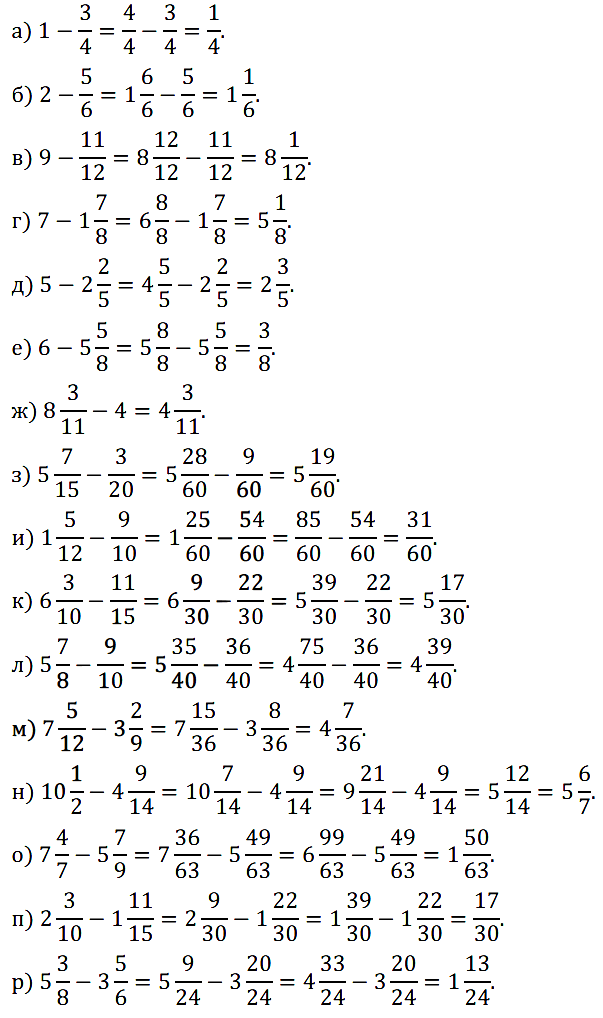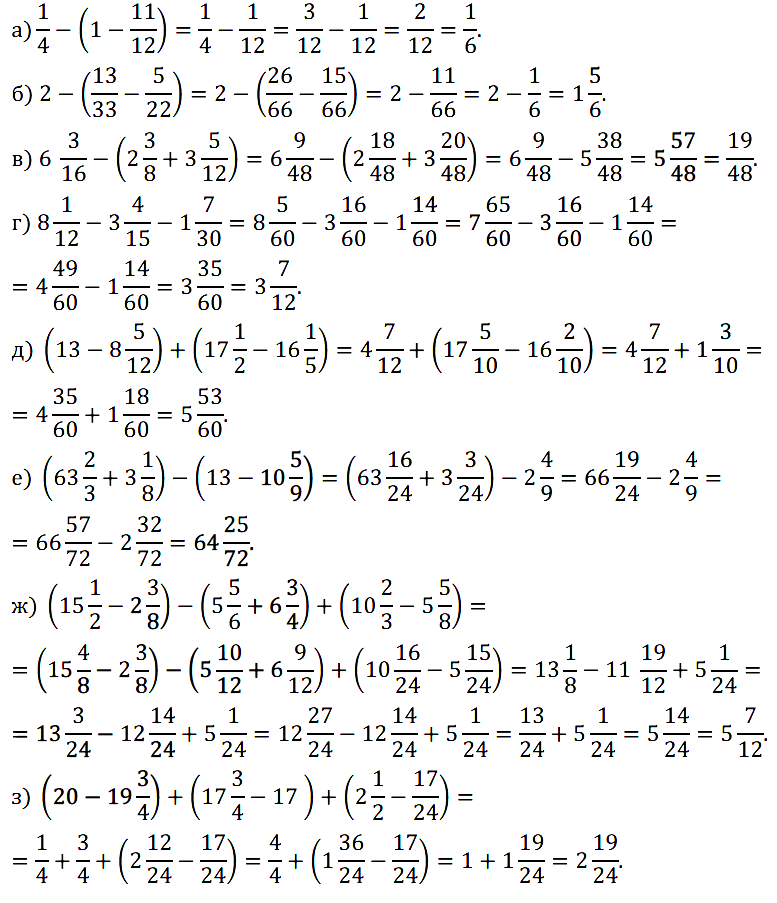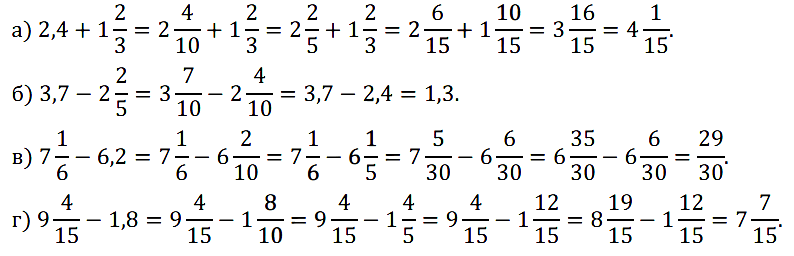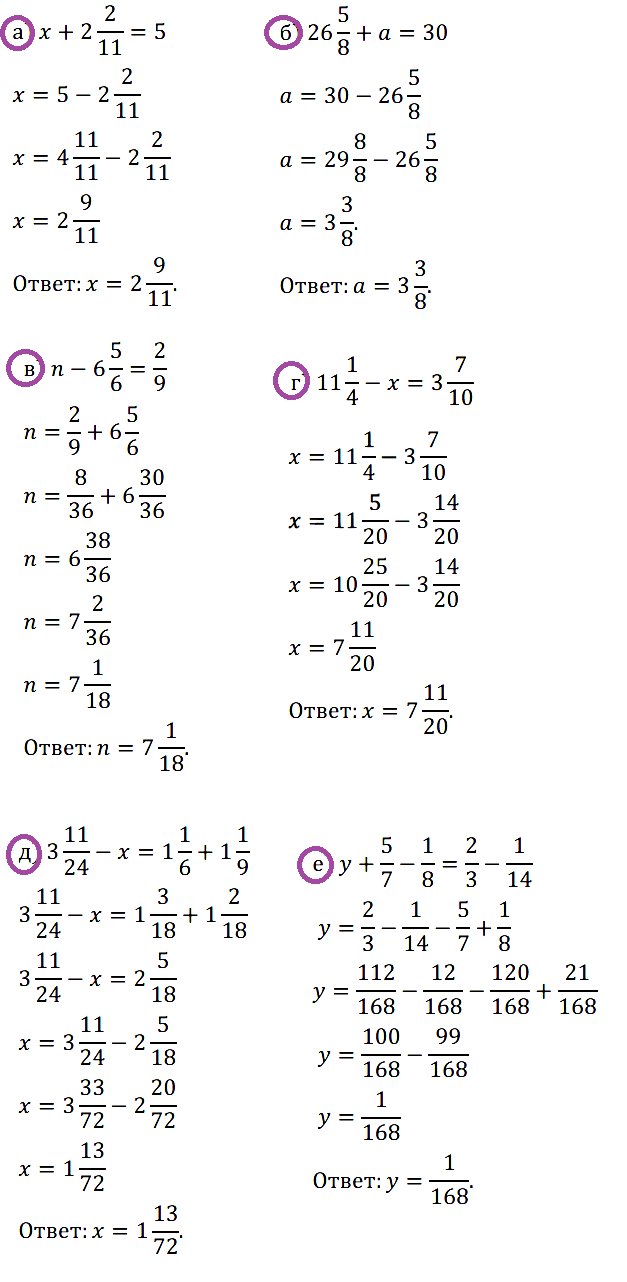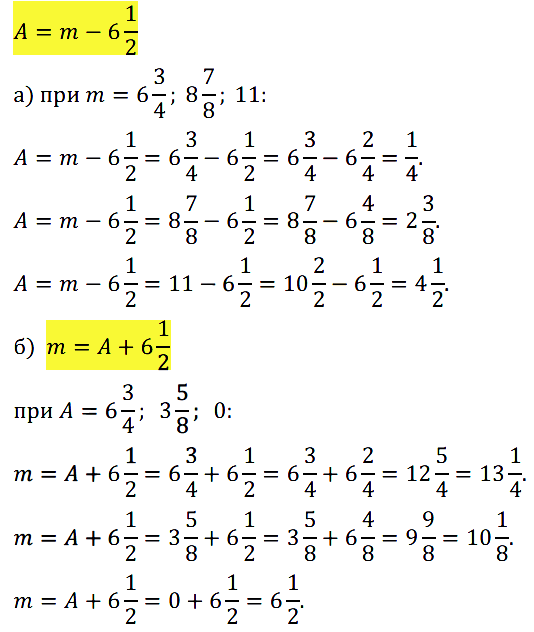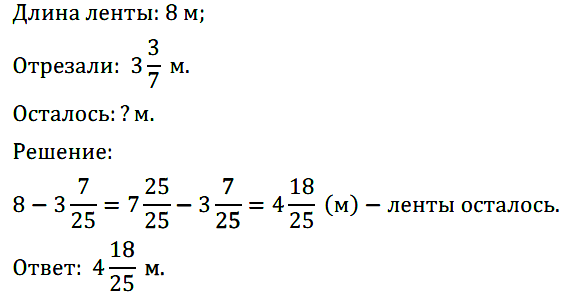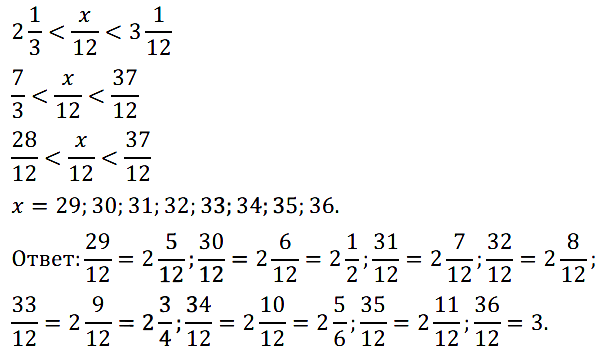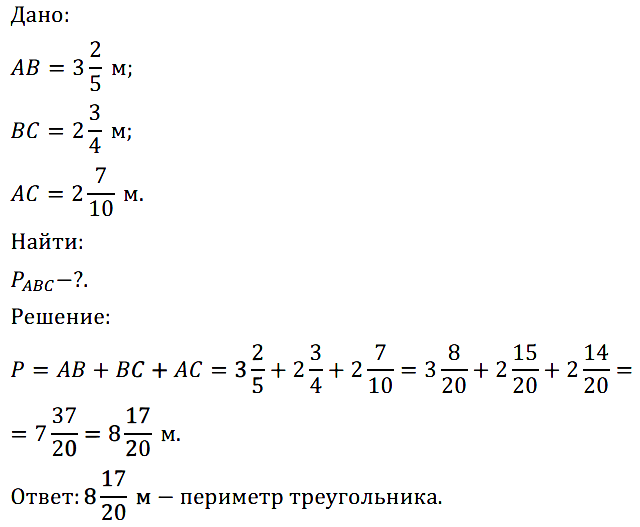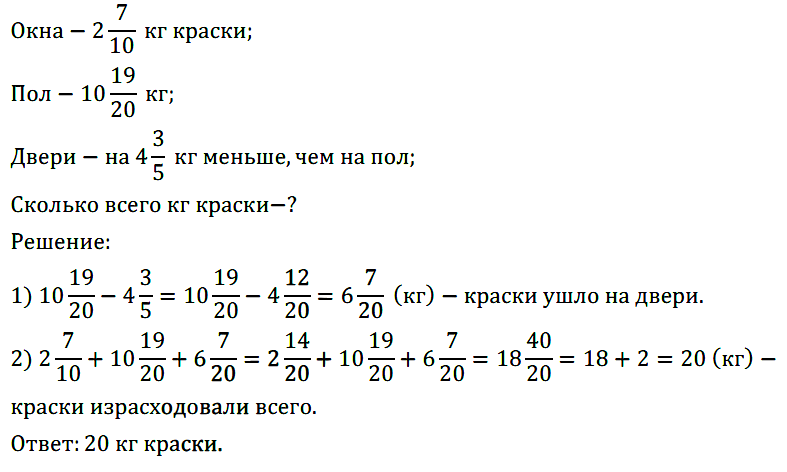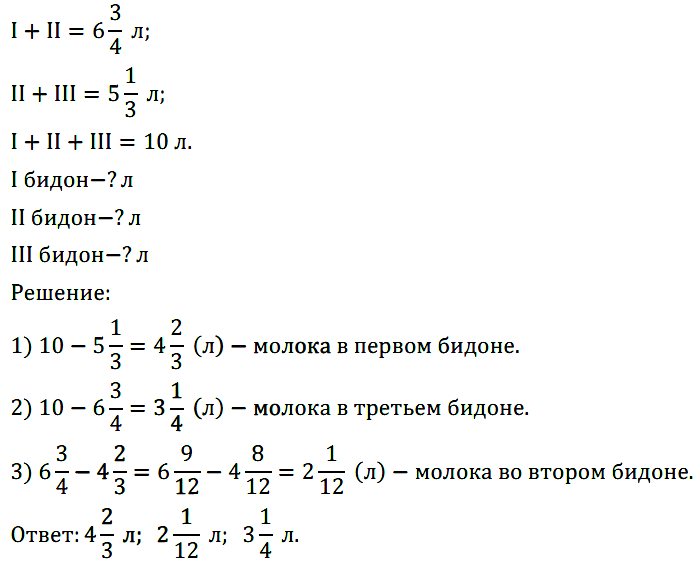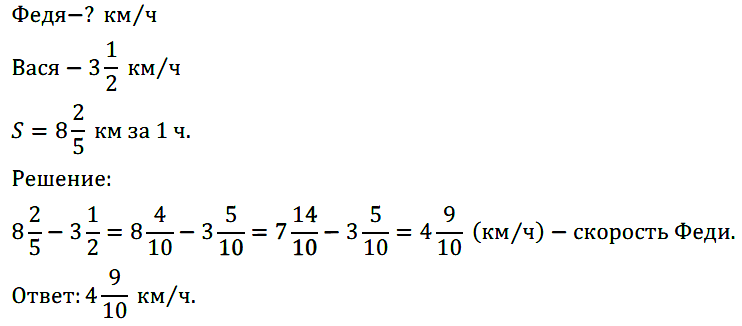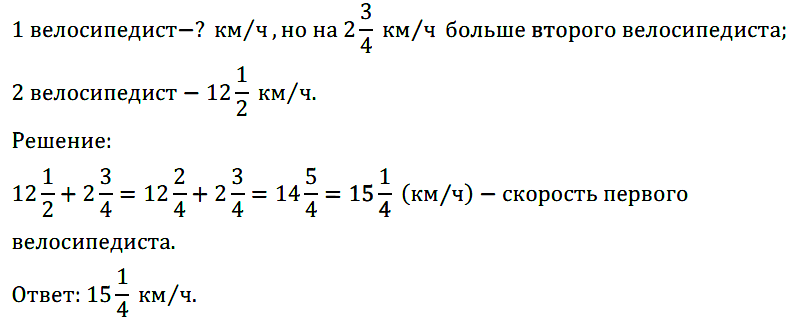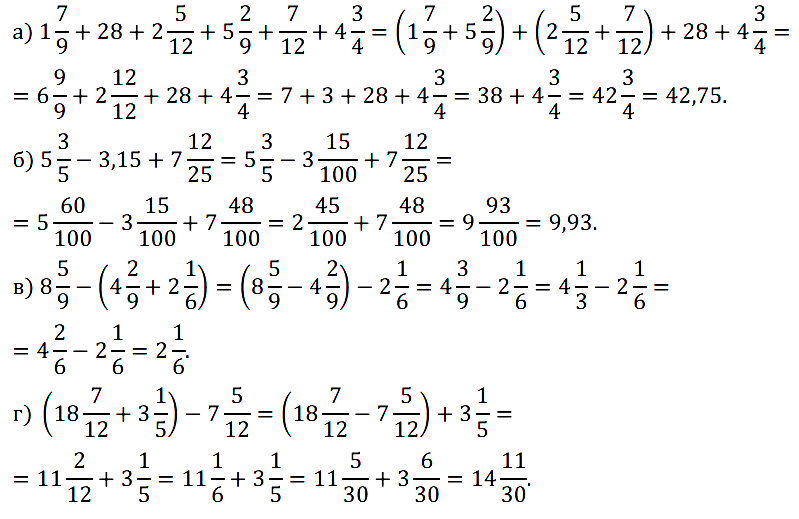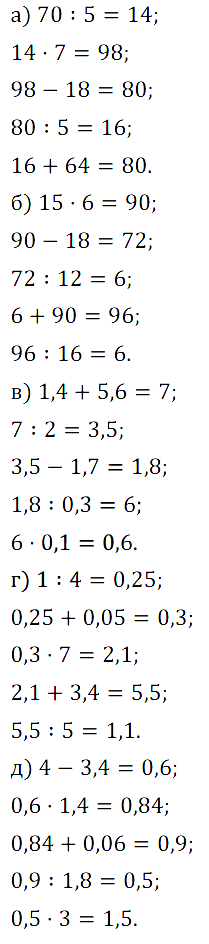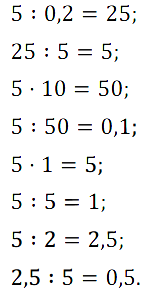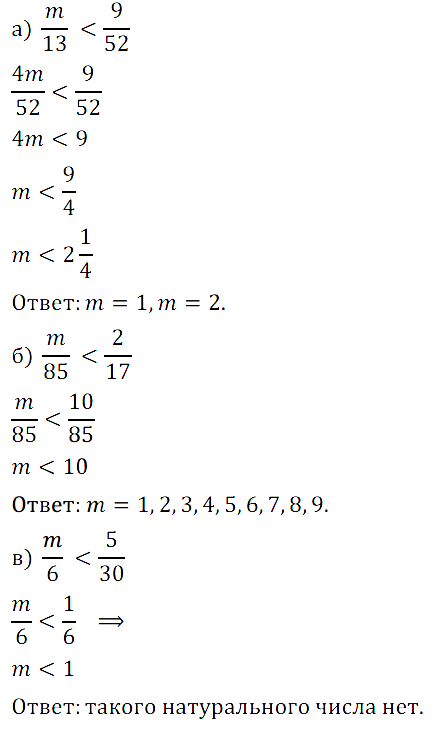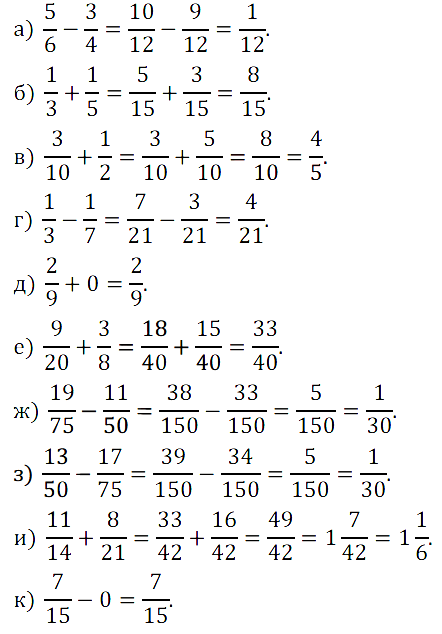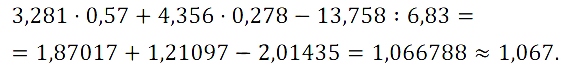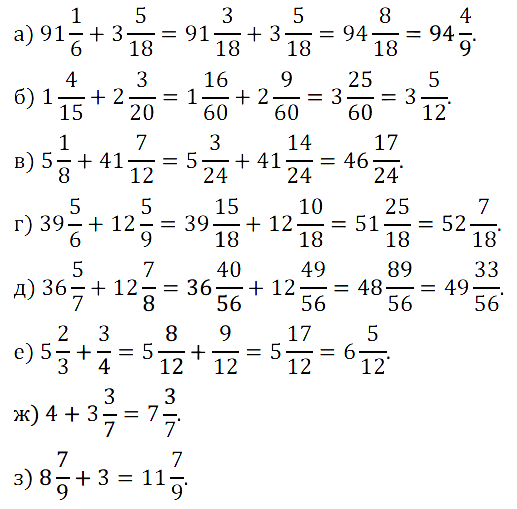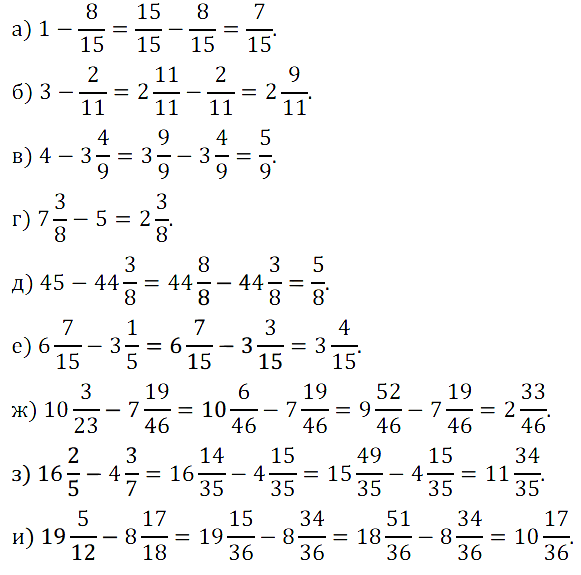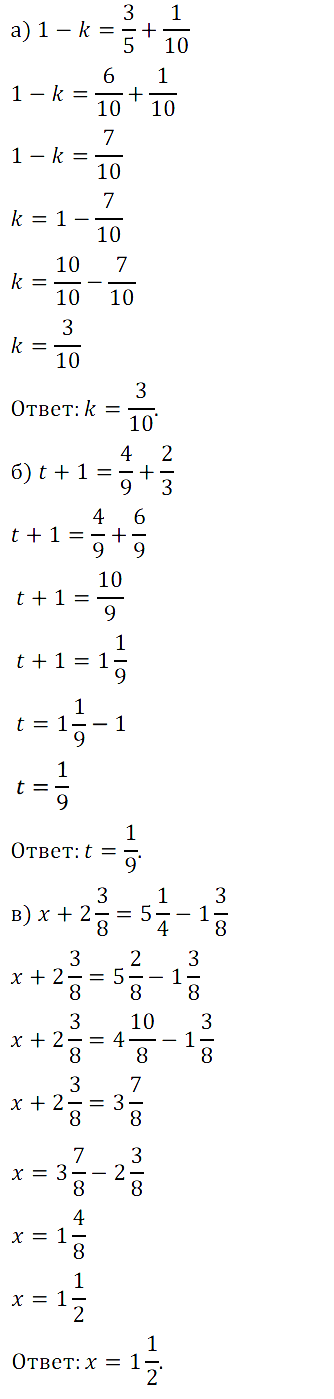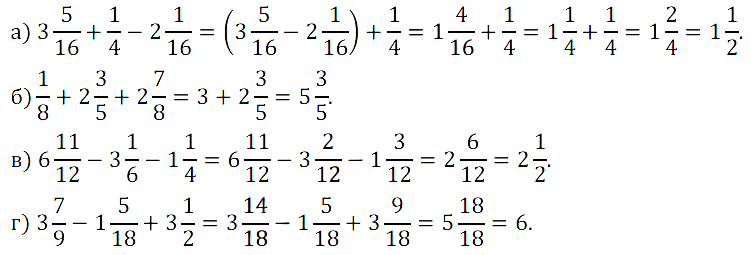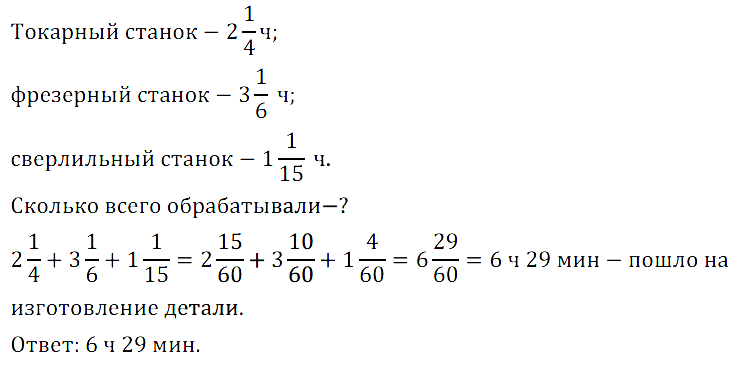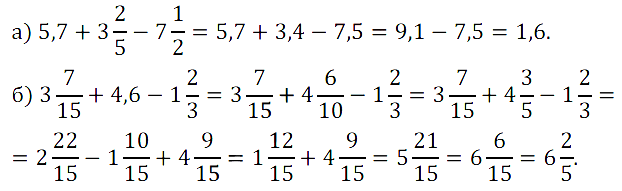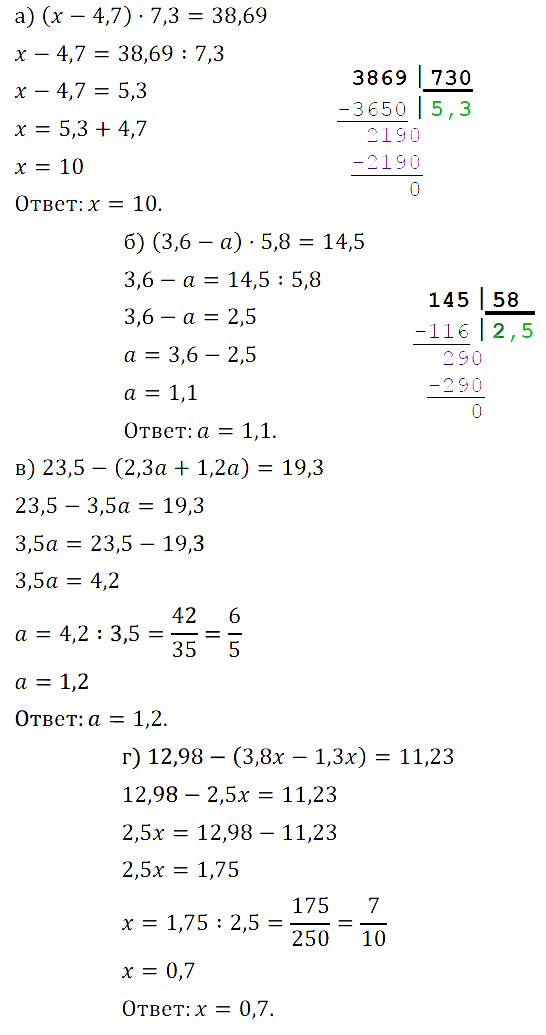Матроскин же выяснил что в эту бочку входит 38 бидонов
Учебник Моро 2 класс. 1 часть. Страница 62
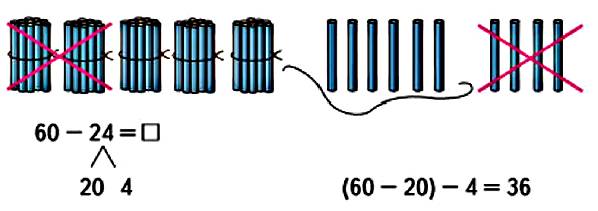
1. Вычисли устно с объяснением.
Представим вычитаемое в виде суммы разрядных слагаемых и получим выражение из трех чисел. Сгруппируем их для удобства так, чтобы из единиц можно было вычесть единицы, а из десятков десятки.
70 − 28 = 70 − (20 + 8) = (70 − 20) − 8 = 50 − 8 = 42
30 − 23 = 30 − (20 + 3) = (30 − 20) − 3 = 10 − 3 = 7
Задание 2.
50 − 46 = 50 − (40 + 6) = (50 − 40) − 6 = 10 − 6 = 4
70 − 38 = 70 − (30 + 8) = (70 − 30) − 8 = 40 − 8 = 32
50 − 6 = (40 + 10) − 6 = 40 + (10 − 6) = 40 + 4 = 44
70 − 8 = (60 + 10) − 8 = 60 + (10 − 8) = 60 + 2 = 62
90 − 24 = 90 − (20 + 4) = (90 − 20) − 4 = 70 − 4 = 66
94 − 20 = (90 + 4) − 20 = 4 + (90 − 20) = 4 + 70 = 74
100 − 2 = (90 + 10) − 2 = 90 + (10 − 2) = 90 + 8 = 98
100 − 38 = 100 − (30 + 8) = (100 − 30) − 8 = 70 − 8 = 62
3. Реши задачи разными способами.
1) В одной бочке было 20 ведер воды, а в другой − 15 ведер. Для полива взяли 5 ведер воды. Сколько ведер воды осталось в бочках?
1) 20 + 15 = 35 (ведер) − воды было всего;
2) 35 − 5 = 30 (ведер) − воды осталось в двух бочках.
1) 20 − 5 = 15 (ведер) − воды осталось в первой бочке;
2) 15 + 15 = 30 (ведер) − воды осталось в двух бочках.
2) В кувшине было 12 стаканов молока. На кашу пошло 5 стаканов молока, а на омлет − 2 стакана. Сколько стаканов молока осталось в кувшине?
1) 5 + 2 = 7 (стаканов) − молока потратили;
2) 12 − 7 = 5 (стаканов) − молока осталось.
1) 12 − 5 = 7 (стаканов) − молока осталось после приготовления каши;
2) 7 − 2 = 5 (стаканов) − молока осталось после приготовления омлета.
4. Запиши выражения и вычисли их значения.
1) Из числа 80 вычесть сумму чисел 53 и 7.
80 − (53 + 7) = 80 − 60 = 20
2) Из числа 90 вычесть разность чисел 84 и 4.
90 − (84 − 4) = 90 − 80 = 10
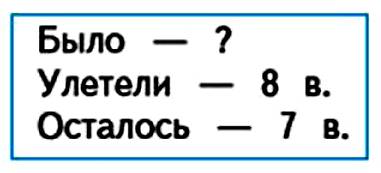
5. Составь по краткой записи задачу и реши ее.
На дереве сидели сороки. После того, как улетело 8 сорок, на дереве осталось сидеть 7 сорок. Сколько всего сорок было на дереве?
7 + 8 = 15 (ворон) − всего сидело на дереве.
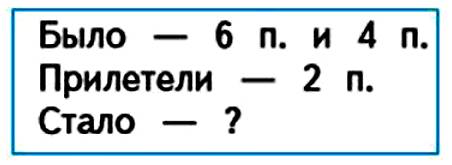
На одной ветке сосны сидели 6 птиц, а на другой — 4. Прилетели ещё 2 птицы и сели на сосну. Сколько птиц стало на сосне?
Задание 6
12 мм 1 м
26 дм > 10 дм
1 ч > 59 мин
60 мин > 59 мин
1 м > 59 см
100 см > 59 см
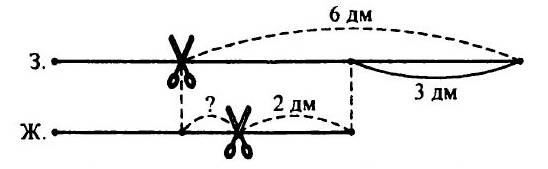
7. У Ани две ленты: зеленая и желтая. Зеленая лента на 3 дм длиннее желтой. Аня отрезала от зеленой ленты 6 дм, а от желтой 2 дм. Какая лента стала длиннее? На сколько сантиметров?
1) 6 − 2 = на 4 (дм) − Аня отрезала от зеленой ленты больше, чем от желтой;
2) 4 − 3 = 1 (дм), значит на 10 см желтая лента стала длиннее зеленой.
Ответ: желтая лента стала длиннее зеленой на 10 см.
Математика 6 Виленкин. Задачи 381-431
Упражнения №№ 381-431 по математике в 6 классе из учебника УМК Виленкин с ответами. § 2. Сложение и вычитание дробей с разными знаменателями. 12. Сложение и вычитание смешанных чисел. Математика 6 Виленкин. Задачи 381-431. Цитаты из учебника использованы в учебных целях. Ответы адресованы родителям.
Математика 6 класс Виленкин
12. Упражнения 381-431.
№ 381. Выполните сложение: а) 3 2 /7 + 5 3 /14; б) 5 7 /8 + 2 5 /12; в) 7 3 /8 + 1 5 /6; …
№ 382. Выполните вычитание: а) 1 – 3/4; б) 2 – 5/6; в) 9 – 11/12; г) 7 – 1 7 /8; …
№ 383. Найдите значение выражения: а) 1/4 – (1 – 11/12); б) 2 – (13/33 – 5/22); …
№ 384. Выполните действие: а) 2,4 + 1 2 /3; б) 3,7 – 2 2 /5; в) 4 1 /6 – 6,2; г) 9 4 /15 – 1,8.
№ 385. Решите уравнение: а) х + 2 2 /11 = 5; б) 26 5 /8 + а = 30; …
№ 386. Найдите по формуле А = m – 6 1 /2:
а) значение А, если m = 6 3 /4; 8 7 /8; 11; б) значение m, если А = 6 3 /4; 3 5 /8; 0.
№ 387. Школьный бассейн наполняется через первую трубу за 4 ч, а через вторую — за 6 ч. Какую часть бассейна останется наполнить после совместной работы обеих труб в течение часа?
№ 388. Новая машина может выкопать канаву за 8 ч, а старая — за 12 ч. Новая машина работала 3 ч, а старая 5 ч. Какую часть канавы осталось выкопать?
№ 389. От ленты длиной 8 м отрезали кусок длиной 3 7 /25 м. Найдите длину оставшейся части.
№ 390. Одна шахматная партия длилась 11/12 ч, а другая — 5/6 ч. Сколько времени длилась третья партия, если на все три партии было затрачено 3 ч?
№ 391. Когда от верёвки отрезали кусок, то оставшаяся часть имела длину 2 м. Какой длины была бы оставшаяся часть, если бы от верёвки отрезали на 2/5 м меньше? на 3/4 м больше?
№ 392. Запишите все числа, знаменатель дробной части которых равен 12, большие 2 1 /3 и меньшие 3 1 /12.
№ 393. На координатном луче отмечена точка А (m/n) (рис. 17). Отметьте на луче точки, координаты которых равны:
a) 1 + m/n; б) 2 – m/n; в) 2 + m/n; г) 1 + 1 m /n.
№ 394. Найдите периметр треугольника АВС, если АВ = 3 2 /5 м, ВС = 2 3 /4 м и АС = 2 7 /10 м.
№ 395. На одной машине 4 7 /10 т груза, а на другой — на 1 2 /5 т меньше. Сколько тонн груза на двух машинах?
№ 396. В одном ящике 5 3 /10 кг винограда, что на 2 4 /5 т кг меньше, чем в другом ящике. Сколько килограммов винограда в двух ящиках?
№ 397. На окраску оконных рам израсходовали 2 7 /10 кг краски, на окраску пола пошло 10 19 /20 кг, а на окраску дверей потребовалось на 4 3 /5 кг меньше, чем на окраску пола. Сколько всего израсходовали краски?
№ 398. Три бригады вырастили горох на площади 72 19 /20 га. Первая и вторая бригады вырастили горох на площади 44 3 /4 га, а вторая и третья — на площади 52 9 /20 га. Найдите площадь каждого участка.
№ 399. На сахарный завод в понедельник привезли 212 1 /2 т свёклы, во вторник — на 297 1 /5 т больше, чем в понедельник, а в среду — на 114 2 /5 т меньше, чем во вторник и понедельник вместе. Из 7 т свёклы получается 1 т сахара. Сколько сахара получится из привезённой свёклы?
№ 400. В трёх бидонах 10 л молока. В первом и втором бидонах было 6 3 /4 л, а во втором и третьем — 5 1 /3 л молока. Сколько литров молока было в каждом бидоне?
№ 401. Теплоход по течению реки проходит 33 3 /8 км за 1 ч. Скорость течения 2 1 /2 км/ч. Найдите скорость теплохода против течения.
№ 402. Скорость катера по течению реки 17 1 /2 км/ч, а против течения 12 1 /2 км/ч. Какова скорость течения?
№ 403. Федя и Вася шли навстречу друг другу. Каждый час расстояние между ними уменьшалось на 8 2 /5 км. Найдите скорость Феди, если скорость Васи 3 1 /2 км/ч.
№ 404. Первый велосипедист догонял второго, причём расстояние между ними уменьшалось каждый час на 2 3 /4 км. С какой скоростью ехал первый велосипедист, если второй ехал со скоростью 12 1 /2 км/ч?
№ 405. Найдите значение выражения: а) 1 7 /9 + 28 + 2 5 /12 + 5 2 /9 + 7/12 + 4 3 /4; б) 5 3 /5 – 3,15 + 7 12 /25; …
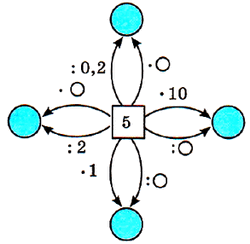
№ 407. Найдите пропущенные числа на рисунке:
№ 408. Найдите натуральные значения m, при которых верно неравенство:
а) m/13 Нажмите на спойлер, чтобы увидеть ОТВЕТ
№ 409. На сколько процентов увеличится объём куба, если длину каждого его ребра увеличить на 20 %?
№ 410. Почтовый самолёт поднялся с аэродрома в 10 ч 40 мин утра, пробыл в полёте 5 ч 15 мин, а на земле во время стоянки 1 ч 37 мин. Когда самолёт вернулся на аэродром?
№ 411. Выполните действие: а) 5/6 – 3/4; б) 1/3 + 1/5; в) 3/10 + 1/2; …
№ 412. Четырёхугольник с равными сторонами называют ромбом (рис. 18). Подумайте, является ли ромб правильным многоугольником. В чём сходство решения этой задачи с нахождением решений двойного неравенства 0 Нажмите на спойлер, чтобы увидеть ОТВЕТ
№ 413. Докажите переместительное и сочетательное свойства сложения для дробей с одинаковыми знаменателями на основе таких же свойств для натуральных чисел.
№ 414. Три сына хана получили в наследство большую отару овец. Старшему сыну достались 25 частей стада, среднему — 10 частей, а младшему — 1 часть. Сколько овец было в отаре, если средний брат получил на 765 овец больше, чем младший?
№ 415. В городе семизначные телефонные номера. Сколько в нём может быть номеров, начинающихся цифрами 235?
№ 416. Выполните вычисления с помощью микрокалькулятора и результат округлите до тысячных: 3,281 • 0,57 + 4,356 • 0,278 – 13,758 : 6,83.
№ 417. Решите задачу:
1) Для борьбы с вредителями садов готовится известково–серный отвар, состоящий из 6 частей серы, 3 частей негашёной извести и 50 частей воды (по массе). Сколько получится килограммов отвара, если воды взять на 8,8 кг больше, чем серы?
2) Для приготовления фарфора на 1 часть гипса берут 2 части песка и 25 частей глины (по массе). Сколько получится килограммов фарфора, если взять глины на 6,9 кг больше, чем песка?
№ 418. Выполните действия:
1) 7225 : 85 + 64 • 2345 – 248 838 : 619;
2) 54 • 3465 – 9025 : 95 + 360 272 : 712.
№ 419. Выполните действие: а) 91 1 /6 +3 5 /18; б) 1 4 /15 + 2 3 /20; в) 5 1 /8 + 41 7 /12; …
№ 420. Найдите значение разности: а) 1 – 8/15; б) 3 – 2/11; в) 4 – 3 4 /9; …
№ 421. Решите уравнение: а) 1 – k = 3/5 + 1/10; б) t + 1 = 4/9 + 2/3; в) x + 2 3 /8 = 5 1 /4 – 1 3 /8.
№ 422. Найдите значение выражения: а) 3 5 /16 + 1/4 – 2 1 /16; б) 1/8 + 2 3 /5 + 2 7 /8; …
№ 423. Один тракторист вспахал 2/9 поля, а другой — 2/3 того же поля. Какую часть поля осталось вспахать?
№ 424. Бочки горючего хватает для работы одного двигателя на 7 ч, а другого — на 5 ч. Какая часть горючего останется от полной бочки после 2 ч работы первого двигателя и 3 ч работы второго двигателя?
№ 425. Для экспедиции, работающей в тайге, сбросили с вертолёта упаковку с продуктами, которая упала на землю через 3 с. С какой высоты была сброшена эта упаковка, если в первую секунду она пролетела 4 9 /10 м, а в каждую следующую секунду она пролетала на 9 4 /5 м больше, чем в предыдущую?
№ 426. Сколько времени пошло на изготовление детали, если её обрабатывали на токарном станке 2 1 /4 ч, на фрезерном станке 3 1 /6 ч и на сверлильном станке 1 1 /15 ч?
№ 427. Найдите значение выражения: а) 5,7 + 3 2 /5 – 7 1 /2; б) 3 7 /15 + 4,6 – 1 2 /3.
№ 428. Из одного пункта одновременно в противоположных направлениях вышли два пешехода. Через 1,5 ч расстояние между ними было 12,3 км. Скорость одного пешехода 4,4 км/ч. Найдите скорость другого пешехода.
№ 429. Для приготовления варенья из вишни на 3 части сахара берут 2 части ягод (по массе). Сколько килограммов сахара и сколько килограммов ягод надо взять, чтобы получить 10 кг варенья, если при варке его масса уменьшается в 1,5 раза?
№ 430. Найдите значение выражения:
а) (44,96 + 28,84 : (13,7 – 10,9)) : 1,8;
б) 102,816 : (3,2 • 6,3) + 3,84.
№ 431. Решите уравнение:
а) (х – 4,7) • 7,3 = 38,69; б) (3,6 – а) • 5,8 = 14,5; в) 23,5 – (2,3а + 1,2а) = 19,3; г) 12,98 – (3,8x – 1,3x) = 11,23.
Умники и умницы
Умные дети — счастливые родители
ПНШ 4 класс. Математика. Тетрадь для самостоятельной работы № 1, с. 69
Литр. Сколько литров?
Ответы к с. 69
127. Определи стоимость:
а) кваса, налитого в трёхлитровый бидон, если его цена 30 руб./л;
2) 30 • 3 = 90 (руб.)
О т в е т: стоимость кваса 90 рублей.
б) бензина, налитого в сорокалитровый бак автомобиля и в две десятилитровые канистры, если цена бензина 32 руб. 50 коп. за литр.
1) 40 + 10 • 2 = 60 (л) — бензина всего
2) 32 руб. 50 коп. • 60 = (32 руб. + 50 коп.) • 60 = 32 руб. • 60 + 50 коп. • 60 = 1920 руб. + 3000 коп. = 1920 руб. + 30 руб. = 1950 руб.
О т в е т: стоимость бензина 1950 рублей.
128. Реши задачи. Вычисли и запиши ответ каждой задачи.
а) В двух бочках 72 л кваса. Когда из первой бочки взяли 14 л кваса, в ней осталось 26 л. Сколько литров кваса было в каждой бочке сначала?
1) 26 + 14 = 40 (л) — в первой бочке
2) 72 — 40 = 32 (л) — во второй бочке
О т в е т: I бочка — 40 литров кваса, II бочка — 32 литра кваса.
б) В трёх одинаковых бидонах 93 л молока. Сколько литров молока в пяти бидонах такой же вместимости?
93 : 3 • 5 = 155 (л)
О т в е т: в пяти бидонах 155 литров молока.
в) В бочке на 24 л кваса больше, чем в бидоне. Сколько литров кваса в бидоне, если в бочке его в 5 раз больше, чем в бидоне?
1) 5 – 1 = 4 (ч.) – разница
2) 24 : 4 = 6 (л) – кваса в одном бидоне
О т в е т: в бидоне 6 литров кваса.
Головоломка про бочку+задача на логику
Представьте, что у вас есть бочка, в которую залита вода приблизительно до половины. Вам необходимо проверить, на самом деле ли она наполнена точно до середины, и у вас нет никаких подручных приспособлений, чтобы это сделать. Каким же образом можно проверить, до какого уровня вода залита в бочку?
Но при этом существует некоторый логический парадокс. По сути, полупустой бочонок — ровно то же самое, что и полуполный. А раз обе части этой бочки равны друг другу, получается, что и целые тоже одинаковы. И так как пустая наполовину ёмкость равняется наполовину заполненной, то и пустой бочонок будет равняться полному. Но как же получается этот вывод?
Отрывок из книги Якова Исидоровича Перельмана «101 головоломка».
Лига образования
1.9K постов 16.6K подписчиков
Правила сообщества
Публиковать могут пользователи с любым рейтингом. Однако мы хотим, чтобы соблюдались следующие условия:
-уважение к читателю и открытость
-публикация недостоверной информации
-конструктивные дискуссии на тему постов
-личные оскорбления и провокации
-неподкрепленные фактами утверждения
Объем пустой бочки равен объему полной бочки.
наклонить набок так чтобы вода образовала диагональ между краем и местом где сходится дно и стенка
работает только с циллиндрическими бочками и кастрюлями
И так как пустая наполовину ёмкость равняется наполовину заполненной, то и пустой бочонок будет равняться полному.
Стуком? по конденсату?
если не брать в расчет мозгортах а-ля апории зенона из воторй части задачи то очеьн просто: наклонить бочку, пока вода не дойдет до переднего края. если бочка наполнена наполовину, то в этот момент уровень воды с дальней стороны бочки будет на стыке дна и дальней стенки
наклонить по диагонали. от краюшка верхнего до краюшка нижнего будет вода если полуполный.
Найти величину гипотенузы, пользуясь только знаниями семиклассника
Задача не сложная для старшеклассника, но у семиклассника пока нет полного набора инструментов, который делают это задачу лёгкой, поэтому надо учиться думать.
Могильная головоломка
Недавно заинтересовался механическими головоломками и понял, что это отдельный мир, где возможны разнообразнейшие механические извращения.
Вот одно из них: из могилы нужно вытянуть крест 🙂
Делал все из алюминия и бронзы, на изготовление ушло пару дней с отвлеканием на основную работу. Работа достаточно простая, но вся суть в механике открывания. Могильный камень из алюминия получился достаточно увесистым 🙂
Помогите найти гребаную лошадь
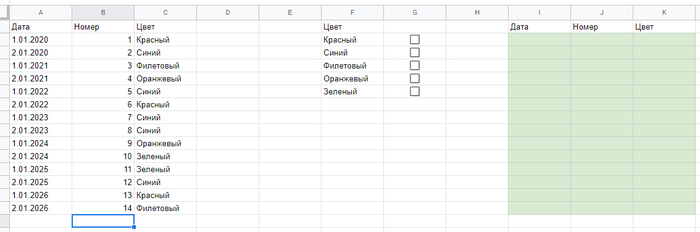
GSQ1 Задачки в гугл таблицах // Проба пера
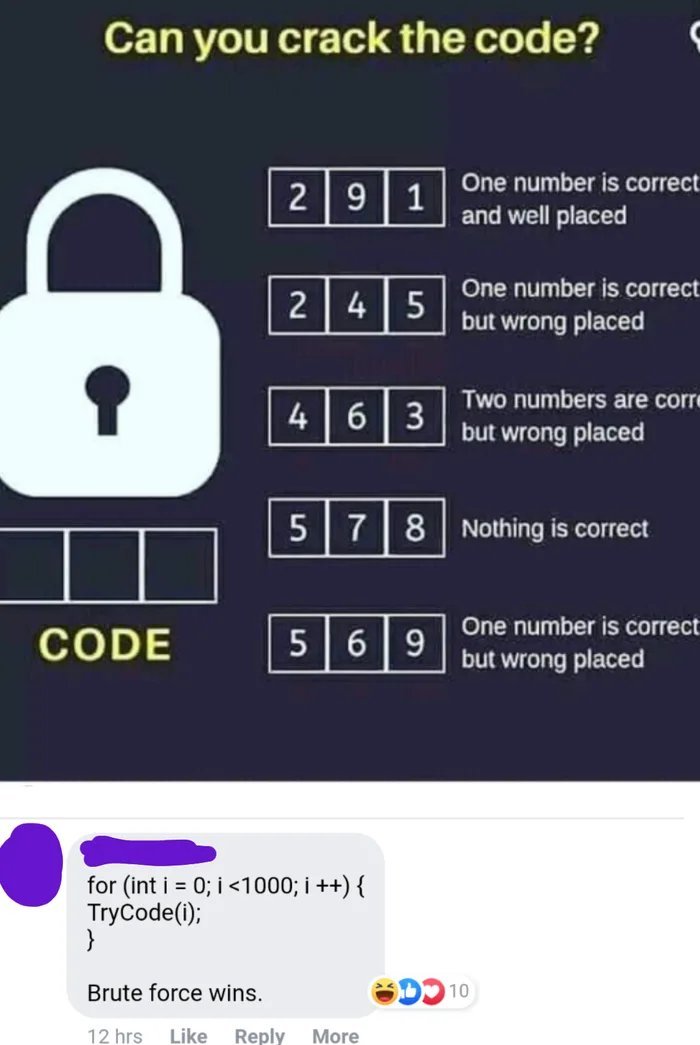
Подбери код от замка
Найди кота
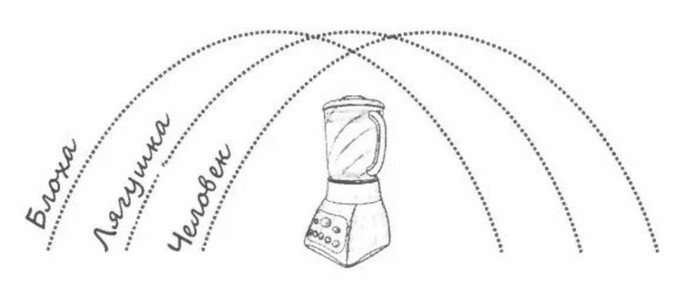
Загадка про блендер
«Вас уменьшили до размеров 5-центовой монеты и бросили в блендер. Ваш вес уменьшился так, что плотность вашего тела осталась прежней. Лезвия начнут вращаться через 60 секунд. Ваши действия?»
Начнём с классификации наиболее популярных ответов, затем расскажем про тот, который считается лучшим среди интервьюверов в Google.
Многие соискатели выдают один забавный ответ: «Так как блендер очень скоро включат, можно предположить, что в него положат какие-то продукты, и поэтому мне, может быть, лучше подставить свою шею под лезвие, чем задохнуться из-за паров той жижи, которая скоро появится в блендере».Если же говорить о часто встречающихся серьезных ответах, то лидерами являются такие.
Первый. Лечь как можно плотнее к днищу, чтобы лезвия крутились надо мной.
Второй. Встать с той стороны блендера, где крепятся лезвия. Возможно, между стенкой и устройством крепления есть зазор шириной в 5-центовую монету.
Третий. Залезть по лезвию на ось вращения и найти такое место, где при вращении лезвий можно сохранять равновесие. Схватиться покрепче. Итоговая центростремительная сила в этом случае будет близка к нулю, что и позволит удержаться.
Первые три варианта дают некоторый шанс на выживание, но что если лезвия будут крутиться долго? Или конструкция такова, что вас всё таки заденет остриём? И вообще, если вдуматься, кто и зачем вас бросил в блендер? Если это какие-то враждебные существа, которые собираются приготовить соус из человека, то ваши долгосрочные шансы на выживание будут очень небольшими при любом варианте.
Вот стандартные ответы интервьюверов на уточняющие вопросы: «По поводу враждебных существ не беспокойтесь». «Никакой жидкости добавлено не будет». «Крышки у блендера нет». «Исходите из того, что лезвия будут вращаться до тех пор, пока вы не погибните».
Четвертый подход отличается — нужно выбраться во вне. Интервьювер поинтересуется, как вы будете это делать. Одним из самых ярких ответов был такой: при очень малом весе вы сможете взобраться по стенке примерно так же, как это делают мухи.
Пятый, не самый оптимистичный, вариант — воспользоваться телефоном и позвонить или отправить sms с просьбой о помощи. Тут всё зависит от того, уменьшился ли так же ваш телефон, сможет ли он работать с базовой станцией (которая осталась прежней) и какова будет скорость реакции службы спасения (и будет ли вообще?).
Шестой вариант: разорвать одежду на полосы, чтобы сделать из них верёрвку и воспользоваться её, чтобы выбраться. Но реально ли это сделать за одну минуту? Как крепить верёвку сверху? И даже если это удастся, как потом спуститься вниз?
Есть и седьмой: использовать одежду и собственные усилия, чтобы как-то заблокировать (или даже сломать) лезвия или работу мотора. Но и здесь могут возникнуть проблемы.
Ни один из перечисленных ответов не принесёт вам в Google много баллов. Интервьюверы рассказывали, что лучший ответ, который они слышали был таким — выпрыгнуть из блендера.
Ух ты? В вопросе даётся важный ключ — слово «плотность». Эта подсказка наводит на мысль, что важны вес и объем тела (а на другие «нереалистичности» можно не обращать внимания) и что подходящий ответ должен строиться на простейших законах физики.
Короче: интервьювер хочет, чтобы вы сфокусировались на последствиях, связанных с изменением размера. Вы, вероятно, слышали, что муравей способен поднять вес, в 50 раз превышающий вес его тела. Это объясняется не тем, что его мускулы лучше, чем у человека, а тем, что муравей маленький. Вес любого живого существа пропорционален кубу его высоты. Сила мускулов и скелета, поддерживающего их, зависит от площади их поперечного сечения, которая пропорциональна квадрату высоты. Если вас уменьшить до 1/10 вашего роста, сила ваших мускулов уменьшится в сто раз, но ваш вес уменьшится еще больше — в тысячу раз. Про прочих равных условиях небольшие существа «сильнее».
В середине 1600-х годов Джованни Альфонсо Борелли, современник Галилео, предположил, что всё, что прыгает, поднимается примерно на одинаковую высоту. Подумайте хорошенько об этом. Если вы физически здоровы, то, вероятно, сможете подпрыгнуть сантиметров на 70. Эта высота не преграда и для других живых существ: лошади, кролика, лягушки, кузнечика или блохи. Разумеется, есть вариации, но общее правило именно такое: самые крутые баскетболисты NBA могут поднять свой центр тяжести примерно на такую же высоту, как и блоха.
Мускульная энергия в конечном счёте определяется химическими процессами: глюкозой и водородом, циркулирующем в крови, а также АТФ, имеющимся в клетках мускул. Количество любых хим. веществ пропорционально объему вашего тела т.е. если вы уменьшитесь до 1/n вашего размера, то мускульная энергия сократится в n³ раз.
К счастью, вес уменьшится так же. Поэтому при размере в монетку, высота вашего прыжка (если не учитывать сопротивление воздуха) никак не изменится. Высота блендера примерно 30 см. Если вы можете сейчас перепрыгнуть через препятствие такой высоты, то удрать из блендера для вас не будет проблемой.
Возможно, вы спросите, как же упав потом с такой высоты вы не поломаете себе кости? Поверхность, которую вы теперь занимаете, составит 1/n² по сравнению с вами обычным, а вес сократится еще больше, до 1/n³ прежнего. Соотношение площади поверхности к весу возрастёт в n раз, поэтому когда вы приземлитесь, никаких поврежений у вас не будет. Это объясняет, почему любое существо размером с мышь и менее может не беспокоиться и падать с любой высоты.