Медиана балла это что

Что лучше использовать при анализе данных: среднее или медиану?

Сегодня разберем два понятия «среднее» и «медиана».

Для начала задам два вопроса: знакомы ли вы с понятием «медиана»? Знаете ли вы, в чем разница между средним и медианой? Скорее всего, если вы работаете с обзорами по рынку зарплат, вы встречали понятие медианы и чаще всего именно на этом ее применение и заканчивалось. Но я рекомендую использовать медиану и в других случаях.

Среднее – это самый популярный статистический показатель, который используется для измерения центра или середины данных. Среднее значение считается как сумма всех чисел, деленная на общее количество чисел. Это материал где-то пятого класса, поэтому тут пока все просто. Среднее значение в компаниях считают для стажа, возраста сотрудников, зарплаты по грейду, уровню должности, для подачи отчетности по статистическим данным. Считается с помощью функции в Excel: СРЗНАЧ или AVERAGE в английской версии.

Минусы среднего показателя:

Среднее значение может быть не совсем объективным отражением данных, так как на него могут влиять выбросы (очень большие или очень маленькие значения в наборе данных).

Если вы считаете средний стаж работы сотрудников в компании при большой текучести, стаж до трех месяцев работы сотрудников будет занижать данные. Или наоборот, у вас есть сотрудники-старожилы, которые работают с основания компании. При учете их продолжительности стажа вы будете завышать данные, что тоже искажает отчетность.

Пример: рассчитать средний стаж работы сотрудников.

Средний стаж составит 4 года.

Медиана – значение, которое делит отсортированные по возрастанию данных на две равные части. То есть медиана показывает середину ваших данных. Медиана считается как значение, расположенное по середине ряда отсортированных значений. Если в ряду находится нечетное количество данных, например, 5, то медианой будет третье значение. Если четное количество данных, например, 4, то медианой будет (значение 2+ значение 3)/2. То есть среднее значение двух показателей посередине.

Считается с помощью функции в Excel МЕДИАНА или MEDIAN в английской версии. Медиана лишена недостатков среднего значения, на нее не влияют выбросы.

Медиана стажа составит 3 года. Разница между 3 и 4 годами стажа работы все-таки есть.

Если нужно посчитать стаж, возраст, зарплату, считайте не среднее, а медиану. Ну или убирайте выбросы.

Источник

Пример расчета медианы

Пример расчета медианы

План (содержание) работы Пример расчета медианы:

Понятие медианы

Формула расчета медианы

Применяемая для расчета медианы формула зависит от типа ряда распределения. Например, в неинтервальном ряду с четным количеством наблюдений медиана будет являться средним арифметическим значением из двух центральных величин, т.е. если совокупность состоит из десяти элементов, то искомый показатель будет равняться среднему значению пятого и шестого элемента. В случае, когда ряд неинтервальный и количество наблюдений нечетное, то медианным будет значение признака, находящегося в центре ранжированного ряда, т.е. для 11 элементов это будет шестой элемент.

В интервальном ряду распределения для вычисления медианы используют следующую формулу:

Формула расчета медианы

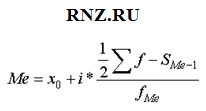
В том случае, если вариационный ряд является дискретным, то медианным будет величина признака в той группе, в которой накопленные частоты превысили половину количества единиц исследуемой совокупности.

Пример расчета медианы в интервальном вариационном ряду

В качестве исходных данных для расчета и анализа медианы используем статистическую группировку банков по величине собственных средств. Таким образом, расчет искомого показателя осуществим на основе следующего интервального ряда распределения:

Источник

Медиана в статистике

Центральную тенденцию данных можно рассматривать не только, как значение с нулевым суммарным отклонением (среднее арифметическое) или максимальную частоту (мода), но и как некоторую отметку (значение в совокупности), делящую ранжированные данные (отсортированные по возрастанию или убыванию) на две равные части. Половина исходных данных меньше этой отметки, а половина – больше. Это и есть медиана.

Итак, медиана в статистике – это уровень показателя, который делит набор данных на две равные половины. Значения в одной половине меньше, а в другой больше медианы. В качестве примера обратимся к набору нормально распределенных случайных чисел.

Очевидно, что при симметричном распределении середина, делящая совокупность пополам, будет находиться в самом центре – там же, где средняя арифметическая (и мода). Это, так сказать, идеальная ситуация, когда мода, медиана и средняя арифметическая совпадают и все их свойства приходятся на одну точку – максимальная частота, деление пополам, нулевая сумма отклонений – все в одном месте. Однако, жизнь не так симметрична, как нормальное распределение.

Допустим, мы имеем дело с техническими замерами отклонений от ожидаемой величины чего-нибудь (содержания элементов, расстояния, уровня, массы и т.д. и т.п.). Если все ОК, то отклонения, скорее всего, будут распределены по закону, близкому к нормальному, примерно, как на рисунке выше. Но если в процессе присутствует важный и неконтролируемый фактор, то могут появиться аномальные значения, которые в значительной мере повлияют на среднюю арифметическую, но при этом почти не затронут медиану.

Медиана выборки – это альтернатива средней арифметической, т.к. она устойчива к аномальным отклонениям (выбросам).

Математическим свойством медианы является то, что сумма абсолютных (по модулю) отклонений от медианного значения дает минимально возможное значение, если сравнивать с отклонениями от любой другой величины. Даже меньше, чем от средней арифметической, о как! Данный факт находит свое применение, например, при решении транспортных задач, когда нужно рассчитать место строительства объектов около дороги таким образом, чтобы суммарная длина рейсов до него из разных мест была минимальной (остановки, заправки, склады и т.д. и т.п.).

Формула медианы

Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.

Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:

№_Me – номер значения, соответствующего медиане,

N – количество значений в совокупности данных.

Тогда медиана обозначается, как

Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:

В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу.

Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.

Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.

Обратимся к наглядной схеме.

Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:

где x_Me — нижняя граница медианного интервала;

i_Me — ширина медианного интервала;

∑f/2 — количество всех значений, деленное на 2 (два);

S_(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;

f_Me — число наблюдений в медианном интервале.

Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%.

Для примера рассчитаем медиану по следующим данным.

Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.

По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.

То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.

Расчет медианы в Excel

Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.

Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:

Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.

Ниже видеоролик о том, как рассчитать медиану в Excel.

Источник

Медиана (статистика)

Также медиану можно определить для случайных величин: в этом случае она делит пополам распределение. Грубо говоря, медианой случайной величины является такое число, что вероятность получить значение случайной величины справа от него равна вероятности получить значение слева от него (и они обе равны 1/2); более точное определение см. ниже.

Можно также сказать, что медиана является 50-м персентилем, 0,5-квантилем или вторым квартилем выборки или распределения.

Связанные понятия

Для определения средних или наиболее типичных значений совокупности используются показатели центра распределения. Основные из них — математическое ожидание, среднее арифметическое, среднее геометрическое, среднее гармоническое, среднее степенное, взвешенные средние, центр сгиба, медиана, мода.

Упоминания в литературе

Связанные понятия (продолжение)

Центра́льные преде́льные теоре́мы (Ц. П. Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.

Т-критерий Вилкоксона — (также используются названия Т-критерий Уилкоксона, критерий Вилкоксона, критерий знаковых рангов Уилкоксона, критерий суммы рангов Уилкоксона) непараметрический статистический тест (критерий), используемый для проверки различий между двумя выборками парных или независимых измерений по уровню какого-либо количественного признака, измеренного в непрерывной или в порядковой шкале.. Впервые предложен Фрэнком Уилкоксоном. Другие названия — W-критерий Вилкоксона, критерий знаковых.

Источник

Исследование моды и медианы результатов ЕГЭ по математике

Рубрика: Математика: алгебра и начала анализа, геометрия

Дата публикации: 04.06.2017 2017-06-04

Статья просмотрена: 719 раз

Библиографическое описание:

Демченко, В. В. Исследование моды и медианы результатов ЕГЭ по математике / В. В. Демченко, Н. А. Кораблев. — Текст : непосредственный // Юный ученый. — 2017. — № 3 (12). — С. 2-4. — URL: https://moluch.ru/young/archive/12/985/ (дата обращения: 11.12.2021).

Для получения более полной характеристики случайных величин кроме средней величины рассчитываются так называемые структурные средние. К ним относят моду и медиану. Данная статья представляет собой результаты исследовательского проекта.

Мода — это наиболее встречающееся значение признака, или, иначе говоря, значение признака, имеющее наибольшую повторяемость (частоту). Моду рассчитывают по-разному, в зависимости от того, как изменяется случайная величина — дискретно или непрерывно.

На практике чаще всего анализируемые данные оформлены в форме таблицы. В случае непрерывно изменяющейся случайной величины все ее значения разбиваются на интервалы по принципу «от и до». Для определения моды в случае непрерывно изменяющейся случайной величины сначала находят модальный интервал, которым является интервал с наибольшей частотой, а затем внутри интервала ведут расчет по формуле:

где — нижняя граница модального интервала;

— величина интервала;

— частота модального интервала;

— частота интервала, предшествующего модальному;

— частота интервала, следующего за модальным.

Определить модальное значение признака можно и по графику. Для этого в случае дискретно изменяющихся случайных величин строится полигон распределения. На оси абсцисс откладываются значения признака, а на оси ординат — соответствующие им частоты. Значение абсциссы, соответствующие наибольшей вершине полигона, будет значением моды.

Для определения моды в случае непрерывно изменяющейся случайной величины строится гистограмма. В этом случае на оси абсцисс находятся значения границ интервалов значений случайной величины, а на оси ординат — соответствующие этим интервалам частоты. На гистограмме модальному интервалу будет соответствовать столбец, имеющий наибольшую высоту. Затем необходимо провести линии, соединяющие вершины модального столбца с прилегающими вершинами соседних столбцов. Для нахождения значения моды из точки пересечения проведенных линий на ось абсцисс опускают перпендикуляр. Абсцисса этой точки и будет модой.

Ряд распределения случайной величины может содержать несколько модальных значений: имеющий одну моду, называется унимодальным, две — бимодальным, три и более — мультимодальным.

Медиана — это значение признака, которое делит все данные на две равные части: половина единиц совокупности имеет значения признака не меньше медианы, другая половина — значения признака не больше медианы.

В случае непрерывно изменяющихся случайных величин сначала определяют медианный интервал. Для этого рассчитывают порядковый номер медианы . Накопленной частоте, присущей медиане (номеру медианного значения признака) соответствует медианный интервал. Обозначим накопленную частоту как . Непосредственно расчет медианы в медианном интервале проводят по формуле:

,

где — нижняя граница медианного интервала;

— величина медианного интервала

— накопленная частота интервала, предшествующего медианному;

частота медианного интервала.

Медиана может быть определена графически по кумуляте. Для этих целей на оси ординат, где отмечаются накопленные частоты, находится точка, соответствующая полусумме всех частот, т. е. порядковому номеру медианы. Из нее проводится прямая параллельно оси абсцисс до пересечения с графиком. Абсцисса точки пересечения и соответствует медиане.

Для определения медианы в случае дискретно изменяющихся случайных величин значения изучаемого признака ранжируют, т. е. располагают в порядке возрастания (или убывания). Если число единиц совокупности нечетное, то значение признака, находящееся в середине ранжированного ряда, будет являться медианой. Если число единиц будет четное, то медианой будет средняя величина из двух значений признака, находящихся в середине ряда.

В качестве практического примера рассмотрим результаты сдачи ЕГЭ по математике некоторой совокупностью учащихся в количестве 170 человек. При этом с некоторым допущением будем считать результат сдачи ЕГЭ непрерывно изменяющейся величиной, т. е. применим соответствующую формулу расчета. Данные представлены в таблице 1.

Данные о результатах сдачи ЕГЭ по математике по 100-бальной шкале

Величина балла по 100-бальной шкале (x_i)

Количество учащихся (f_i)

Источник