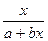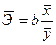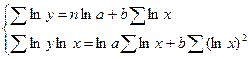Модельные функции линейной модели не всегда являются чем
Что такое «линейная» модель регрессии?
Дата публикации May 29, 2019
Линейная регрессионная модель является одной из простейших моделей в области машинного обучения и статистики. При этом предположение о линейности, лежащее в основе линейной регрессии, часто понимается неточно.
Например, следующие две модели являются моделями линейной регрессии, даже линия с правой стороны не выглядит линейной.
Если это сюрприз, эта статья для вас. В этой статье я пытаюсь объяснить, какая линейность подразумевается за моделями линейной регрессии и почему линейность имеет значение.
Чтобы ответить на эти вопросы, давайте посмотрим, как линейная регрессия работает шаг за шагом, на двух простых примерах.
Пример 1: самая простая модель
Поэтому мы пытаемся смоделировать отношения междуИкса такжеYэтой очень простой линейной функцией. Ключевым моментом здесь является то, что эта функция не только линейна по отношению к входной переменнойИкс, но также линейный по параметрама, б,
Существует множество вариантов выбора функций ошибок, но одним из самых простых является тот, который называется RSS, сумма квадратов ошибок между моделями.F (X)для каждой точки данныхИкси соответствующие целевые значенияY,
С понятием функции ошибки мы можем перефразировать «определить параметрыа, бподбирая обучающие данные наиболее »как« определить параметрыа, бкоторые минимизируют функцию ошибок ».
Давайте вычислим функцию ошибки на наших данных обучения.
Как вы можете инстинктивно догадаться из приведенного выше трехмерного графика, эта функциявыпуклая функция, Оптимизация (нахождение минимума) выпуклой функции намного проще, чем общая математическая оптимизация, поскольку любой локальный минимум всегда является глобальным минимумом в выпуклой функции. (Очень простое объяснение состоит в том, что выпуклые функции имеют только одну минимальную точку, такую как форма «U»). Благодаря этой характеристике выпуклых функций параметры, минимизирующие функцию, можно найти, просто решая уравнения в частных производных следующим образом.
Давайте решим наш случай.
Решая уравнения выше, мы получаема = 5/6, б = 1/2.Итак, наша первая модель (которая минимизирует RSS) получается следующим образом.
Пример 2: Простая соблазнительная модель
Теперь, для тех же точек данных, давайте подумаем о другой модели, как показано ниже.
Как видите, это не линейная функция для ввода переменнойИксбольше. Тем не менее, это все еще линейная функция для параметрова, б,
Как видно выше, уравнение выглядит очень похоже на предыдущее. (Значения коэффициентов различны, но форма уравнения та же.) Визуализация приведена ниже.
Поскольку функция ошибок второй модели также является выпуклой функцией, мы можем найти оптимальные параметры точно такой же процедурой, что и в предыдущем примере.
Решая уравнения выше, мы получаема = 61/618, b = 331/206.Итак, наша вторая модель получается как показано ниже.
Вывод: линейность позади моделей линейной регрессии
2 приведенных выше примера решаются в одной и той же (и очень простой) процедуре, даже если один из них является линейным по отношению к входной переменнойИкси один нелинейныйИкс, Общей характеристикой в 2 моделях является то, что обафункции линейны по параметрама, б Это линейность, принятая за моделями линейной регрессии, и это ключ к математической простоте моделей линейной регрессии.
Выше мы видели только две очень простые модели, но в целом линейность модели по ее параметрам гарантирует, что ее RSS всегда является выпуклой функцией. Это причина, почему мы можем получить оптимальные параметры, решая простые уравнения в частных производных. И именно поэтому линейность имеет значение.
Учебное пособие Допущено Федеральным агентством по образованию в качестве учебного пособия для студентов высших учебных заведений Москва 2006
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
1.5.5. Линейные и нелинейные модели
Такое определение охватывает как статические, так и динамические модели. Применительно к линейным моделям можно также утверждать, что их выход пропорционален входу: чем больше сигнал на входе – тем больше он на выходе. При этом отношение величины выходного сигнала в установившемся режиме к величине входного как раз является коэффициентом пропорциональности.
Линейную статическую характеристику и прохождение сигналов с выхода на вход безынерционного звена, а также искажение выходного сигнала из-за нелинейной статической характеристики типа «насыщение» иллюстрирует рис. 1.5.5.1.
Рис. 1.5.5.1. Линейная и нелинейная статические характеристики.
Однако линейные и нелинейные модели используются не только в технике. Так, например, в фольклоре разных народов существуют поговорки, изречения, передающие народную мудрость, которые также можно рассматривать в качестве семантических моделей.
Примеры линейных моделей: 1) «Чем дальше в лес, тем больше дров»; 2) «По доходу и расход».
Рис. 1.5.5.2. Линейные семантические модели.
В двух первых моделях пропорциональная статическая зависимость выхода от входа может быть проиллюстрирована рисунком 1.5.5.2.
Примеры нелинейных моделей: 3) «Мал золотник, да дорог»; 4) «Велика Федора, да дура». В двух последних моделях нелинейность выражается в обратной пропорциональности выхода входу и может быть отображена на графике статической характеристики так, как показано на рисунке 1.5.5.3.
Рис. 1.5.5.3. Нелинейные семантические модели.
Разумеется, что как линейные, так и разнообразные нелинейные модели находят применение и в других областях. Так, например, в биологии известно, что чем больше вес животного, тем больше пищи оно употребляет для поддержания энергетического баланса (линейная модель) и т.п.


Как правило, реальные объекты и процессы имеют в той или иной степени нелинейный характер, но во многих случаях оказывается возможным осознанно пренебречь нелинейными свойствами для того, например, чтобы воспользоваться хорошо разработанным математическим аппаратом исследования линейных моделей для получения предварительных результатов. Однако делать это нужно осторожно, объективно оценивая погрешности и обосновывая возможность такого упрощения.
Так, например, при тщательном описании оказывается, что фактически любые датчики имеют зону нечувствительности – сугубо типовую нелинейность, которая характеризует тот факт, что при очень малых сигналах на входе даже самый чувствительный измерительный прибор на выходе показывает «нуль», означающий отсутствие входного сигнала. Все зависит от величины этой зоны нечувствительности: в некоторых случаях она так мала, что ей можно пренебречь, и тогда модель становится уже линейной.
1.5.5.1. Преимущества и недостатки линейных моделей
Динамические линейные стационарные системы с сосредоточенными параметрами описываются обыкновенными линейными дифференциальными уравнениями с постоянными коэффициентами.
Системы, исходно нелинейные, но линеаризованные в окрестности опорных траекторий, также описываются с помощью линейных уравнений.
Однако при этом не учитываются важные, интересные, тонкие эффекты, связанные с проявлением нелинейных свойств. Таким образом, линейные модели являются упрощенными по сравнению с нелинейными.
1.5.6. Стационарные и нестационарные модели
Стационарными называют объекты и процессы, параметры которых не изменяются с течением времени. Зачастую стационарность модели является следствием намеренного упрощения описываемого объекта или процесса. Примером стационарной модели может служить дифференциальное уравнение с постоянными, т.е. не зависящими от времени коэффициентами:
Для нестационарной модели важно, что изменения параметров происходят не за любое время вообще, а за время, сопоставимое со временем, в течение которого процесс исследуется, например, за время переходного процесса. Пример нестационарной модели – уравнение с коэффициентами, явно зависящими от времени:

в котором даже одного из коэффициентов 2 t или 4 sin ( t ) вполне достаточно, чтобы модель была нестационарной.
Нестационарные модели являются существенно более сложными, чем стационарные. Аналитическое решение для них оказывается возможным получить только в отдельных, довольно редких случаях. В общем случае исследовать нестационарные модели удается только с помощью численных методов.
1.5.7. Сосредоточенные и распределенные модели
Рис. 1.5.7.1. Изменение температуры в зависимости от времени и от расстояния сечения от нагреваемого конца.
Другие примеры уравнений в частных производных: уравнения диффузии, упругости, электро- и газодинамики.
где D – коэффициент диффузии.
Уравнения непрерывности описывают изменения дырочного и электронного токов в полупроводниковых приборах. Для дырок:
Здесь p – концентрация дырок, n – электронов; q – заряд электрона; J p и J n – плотности дырочного и электронного токов; g p и g n – скорости процессов генерации-рекомбинации дырок и электронов.
Уравнение теплопроводности в общем случае трех пространственных координат (а не только одной, как в случае со стержнем) также записывается через дивергенцию и градиент температуры:
Напомним, что градиент есть векторная функция:
Если обозначить частные производные


1.5.8. Классификация видов моделей
Все рассмотренные выше виды моделей входят в классификацию, приведенную, например, в [5]. Схема классификации приведена на рис. 1.5.8.1.
Рис. 1.5.8.1. Схема классификации видов идеальных и реальных моделей.
На схеме выделены цветом те виды моделей, которые изучаются в данной дисциплине более подробно.
Особенности использования детерминированных и стохастических, дискретных и непрерывных, статических и динамических, стационарных и нестационарных, распределенных и сосредоточенных моделей были рассмотрены выше.
В зависимости от формы представления оригинала, то есть средств, используемых при создании моделей, можно выделить идеальное (абстрактное) и реальное моделирование.
Как правило, аналитический метод применим к относительно простым объектам и процессам или к упрощенным моделям. Как это было показано, например, возможно аналитическое решение линейных стационарных дифференциальных уравнений, но это невозможно в общем случае для нелинейных и/или нестационарных дифференциальных уравнений. Численный метод более универсален и позволяет исследовать по сравнению с аналитическим более широкий класс систем, кроме того, он ориентирован на применение компьютеров. Качественные методы анализа используются, например, в теории автоматического управления для оценки эффективности различных вариантов систем управления.
Имитационные модели отображают все элементарные явления, составляющие моделируемый процесс с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состоянии процесса в определенные моменты времени и оценить характеристики процесса. Основное преимущество имитационного моделирования по сравнению с аналитическим заключается в возможности решения более сложных задач. Имитационные модели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные и нестационарные характеристики элементов, разнообразные случайные воздействия и другие, которые создают зачастую непреодолимые трудности при аналитических исследованиях. В настоящее время имитационное моделирование представляет собой наиболее эффективный метод исследования сложных и больших систем, а иногда и единственный практически доступный метод получения информации о поведении системы, особенно на этапе ее проектирования. Более подробно имитационные модели и методы будут рассмотрены во второй части курса.
При реальном моделировании исследование характеристик объекта производится либо полностью на самом реальном объекте, либо частично на реальном объекте, частично на модели. При этом реальный объект может работать как в нормальном режиме, так и в специальных режимах (в ином масштабе времени или при других значениях параметров и переменных). Хотя реальное моделирование следует признать наиболее адекватным, его возможности весьма ограничены из-за естественных ограничений со стороны реальных объектов. Так, например, проведение реального моделирования сложной автоматизированной системы управления технологическими процессами (АСУТП) потребовало бы, прежде всего создания такой системы, а затем проведения экспериментов с управляемыми объектами, т.е. с технологическими процессами, что в большинстве случаев невозможно в условиях реальных действующих предприятий и в любом случае дорого.
Научный эксперимент отличается широким использованием средств автоматизации при проведении эксперимента, разнообразием средств обработки информации и возможностью вмешательства человека в этот процесс.
Вопросы для самостоятельной проработки к разделу 1.5.
Чем отличаются прагматические модели от познавательных?
Что именно зависит от времени в динамических моделях?
Как получить статическую характеристику из дифференциального уравнения?
При каких условиях можно перейти от стохастической модели к детерминированной?
Что свидетельствует о нелинейности модели в виде дифференциального уравнения?
Что свидетельствует о нелинейности модели в виде статической характеристики?
Какие трудности возникают в связи с использованием нелинейных моделей?
Какие преимущества дает использование нелинейных моделей?
Какие трудности возникают в связи с использованием нестационарных моделей?
Какие преимущества дает использование нестационарных моделей?
Когда целесообразно использовать распределенные модели?
Некоторые регрессионные модели
| № | Вид модели | Уравнение модели | Система нормальных уравнений Гаусса |
| 1. | Линейная | 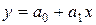 | 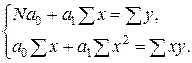 |
| 2. | Параболическая | 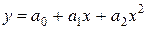 | 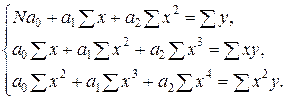 |
| 3. | Кубическая | 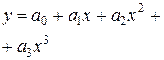 | 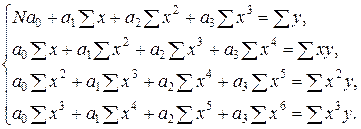 |
| 4. | Гиперболическая | 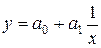 | 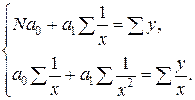 |
| 5. | Показательная | 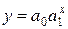 | 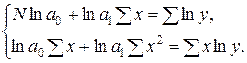 |
| 6. | Степенная | 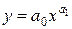 | 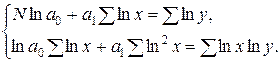 |
| 7. | Логарифмическая | 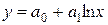 | 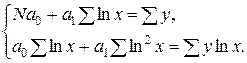 |
Индекс детерминации используется для проверки статистической значимости в целом уравнения нелинейной регрессии по F-критерию Фишера.
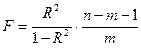
Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n-m-1) – число степеней свободы для остаточной суммы квадратов.
Так для степенной функции вида 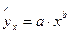
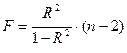
Для параболы второй степени 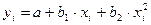
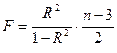
Средняя ошибка аппроксимации – это среднее отклонение расчетных значений результативного признака от фактических: 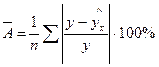
Ошибка аппроксимации в пределах 5-7% свидетельствует о хорошем подборе модели к исходным данным.
Различают 2 класса нелинейной регрессии (НР):
1. Регрессии нелинейные относительно включенных в анализ объясняющих переменных, но линейная по оцениваемым параметрам
2. Регрессии нелинейные по оцениваемым параметрам.
Пример: нелинейная регрессия по включенным в нее объясняющим переменным могут служить следующие функции: полиномы различных степеней, равносторонняя гипербола.
К НР по оцениваемым параметрам относительно следующей модели:
v Показательная у=a×b x × ε
v Экспотенциальная у= e a + bx × ε
Ограничения в использовании полиномов более высоких степеней связаны с требованиями однородности и исследования совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая, и тем менее однородна совокупность по признаку (результирующему).
Парабола второй степени целесообразна к применению, если для определенного интервала значение фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную, или обратная на прямую. В этом случае, определяется значение фактора, при котором достигается максимум (или минимум) значения результативного признака. Приравнивая к нулю первую производную параболы второй степени
Если исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становится трудно интегрируемы, а форма связи часто заменяется другими нелинейными моделями (НМ).
Применение МНК для оценки параметров параболы второго порядка приводит к следующим системам нормальных уравнений:
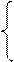
∑yx²= a∑ x²+ b∑ x 3 +c ∑ x 4 ;
Решение ее возможно методом определителей
где ∆- определитель системы,
∆a, ∆b, ∆c – частные определители системы
При b 0,парабола второго порядка симметрична относительно своей низшей точки, что позволяет определить минимум функции в точки, имеющей направление связи, т.е снижение на рост.
Так, если в зависимости от объема выпуска продукции, затраты на производство характеризуется при х=15
В виду симметричности кривой, парабола второй степени далеко не всегда пригодна в конкретном исследовании. Чаще, исследователь имеет дело лишь с отдельными сегментами параболы, а не с полной парабольной формой. Кроме того, параметры парабольной связи не всегда могут быть логически интегрированы.
Поэтому, если график зависимости не демонстрирует четко выраженные параболы второго порядка (нет смены направленности связей-признаков), то она может быть заменена другой нелинейной функцией, например степенной.
В частности, в литературе, часто рассматривается парабола второй степени для характеристики зависимости урожайности от количества внесенных удобрений.
Данная форма связи мотивируется, что с количеством внесенных удобрений урожайность растет лишь до оптимальной дозы вносимых удобрений. Дальнейший же рост их дозы оказывается вредным для растений и урожайность снижается. На несомненную справедливость данного утверждения следует отметить, что внесение в почву минерального удобрения производится на основе учета достижений аэробиологической науки.
Поэтому, на практике, часто данная зависимость представлена лишь сегментом параболы, что и позволяет использовать другие нелинейные функции.
В качестве примера рассмотрим следующую зависимость:
| Внесено минерального удобрения ц. на 1 га | Урожайность ц. на 1 га |
| Х | У |
В соответствии с данными значениями система нормальных уравнений составят:
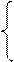
Решая ее методом определителей, получим:
откуда параметры искомого уравнения составят:
а уравнения параболы второй степени примет вид: ŷх=3,4 +2,986х – 0,214 х²
Подставляя в это уравнение последовательно значения Х, найдем теоретические (модельные) значения ŷх Уравнение параболы второго порядка достаточно хорошо описывает рассматриваемую зависимость. Сумма квадратов отклонений остаточных величин: ∑(у- ŷх)²=0,46
Среди класса нелинейных моделей, параметры, которые без особых затруднений оцениваются МНК, следует хорошо известную в эконометрике равностороннюю гиперболу: ŷх=а+(b/x).
Она может быть использована для характеристики связей удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции: временное обращение товаров от величины товарооборота и т.д.
То есть как на микро-, так и на макро- уровне.
Классическим ее примером является кривая Филипса, характеризующая нелинейное соотношение между нормой безработицы Х и % прироста зарплаты У (у=а+(b/х)+ε).
Английский эксперт А.В.Филипс анализирует данные более чем за 100 летний период, в конце 50-х годов 20 века установил обратную зависимость процентного прироста зарплаты от уровня безработицы. Для равносторонней гиперболы всегда у=а+b/х +с, заменив 1/х=z, получим у=а+bz+с, оценка параметров, которая может быть дана МНК. Система нормального уравнения составит:
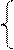
При b>0 имеем обратную зависимость, которая при х → ∞ характеризуется нижней асимптотой, то есть минимальным предельным значением у, оценкой которого служит параметр а. Так для кривой Филипса ŷх=0,00697+0,1842 (1/х) величина параметра а=0,00697 означает, что с ростом уровня безработицы темп прироста зарплаты в пределе стремящимся к 0. Соответственно может определить тот уровень безработицы, при котором зарплата оказывается стабильной и темп ее прироста равен 0.
Данная модель не линейна относительно оцениваемых параметров так как включенные параметры a и b ………… Однако ее можно считать внутренне линейной так как логарифмирование по основанию e приводит его к линейному виду lny = lna+b lnx+lne. Соответствующие оценки параметров a и b могут быть найдены методом наименьших квадратов.
В рассматриваемой степенной функции предполагается, что случайная ошибка e мультипликативно связана с объясняющей переменной. Если же модель представить в виде y = a×x b ×e, то она становится внутреннее не линейной так как ее невозможно привести к линейной.
Внутри не линейная модель вида y = a×x b ×e или 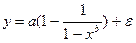
Если модель внутренне не линейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.
Модели внутренне не линейные по параметрам могут иметь место в эконометрических исследованиях, но гораздо большее распространение получили модели, приводимые к линейному виду. Решение такого типа моделей реализовано в прикладных программ. Среди них в частности можно назвать и обратную модель вида: 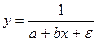
Обращая обе части в равенства, получим линейную форму модели 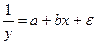
Приводима к линейному виду логическая функция
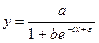
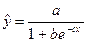
Обращая обе части равенства, получим:
Прологарифмируя обе части по натуральному основанию получим уравнение линейной формы lnb-cx+e=ln(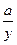
Z=B-cx+e; Z=ln(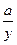
Э=¦¢(x) 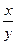
где ¦¢(x)- первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.
Соответственно коэффициент эластичности окажется равным:
Коэффициент эластичности можно определить при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину равную параметру b. В других функциях коэффициент эластичности зависит от значения фактора x. Так для линейной регрессии 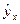
¦¢(x)=b ; Э=b×
В силу того, что коэффициент эластичности для линейной функции не является величиной постоянной, а зависит от соответствующего значения x, то обычно рассчитывают средний показатель эластичности по формуле:
Параметр b определяется из системы, а параметр a – косвенным путем после потенцирования величины логарифма a. Так решая систему нормальных уравнений зависимости спроса от цен, было получено:
Поскольку параметр a экономически не интерпретируется, то нередко зависимость записывается в виде логарифмически – линейной. В виде степенной функции изучается не только эластичность спроса, но и предложения. При этом обычно эластичность спроса характеризуется параметром b 0.
Не смотря на широту использования в эконометрике коэффициентов эластичности возможны случаи, когда их расчет эконометрического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значения в процентах.
В результате обратная модель оказывается внутренне не линейной и преобразовывается методом наименьших квадратов, выполняется не для фактических значений признака, а для обратных величин 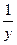
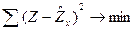
Прологарифмирую, получим lny=a-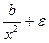
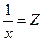
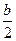
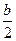
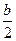
При использовании линеризуемых функций, затрагивающих преобразование переменной y. Следует особенно проверять наличие предпосылок методом наименьших квадратов, чтобы они не нарушились при преобразовании. При не линейных соотношениях рассматриваемых признаков, приводимых к линейному виду, возможно интервальное оценивание параметров не линейной функции.
Sb=
Заключение — до 5 мин.
Содержание и методические рекомендации:
— обобщить наиболее важные, существенные вопросы лекции.
— сформулировать общие выводы.
— поставить задачи для самостоятельной работы.