Модуль вектора скорости что это
Модуль силы, скорости, импульса. Что это?!
В статье разберемся, что такое модуль. Модуль силы, скорости, импульса, что это всё? Давайте разбираться!
Абсолютная величина, известная так же, как модуль, это всегда некое неотрицательное число, чье определение всегда зависит от типа числа. Символически модуль обозначается как: | x |.
Сила и модуль силы
В процессе изучения физики приходится сталкиваться с различными явлениями, рассчитывать скорость, силу и многие другие параметры. Не менее важно понять какими методами, и в каких единицах делаются расчеты по характеристикам этих явлений. Одна из физических величин это сила. Сила представляет собой величину, которая способна показать меру воздействия на тело посредством другого тела или со стороны полей. Взаимодействие образуется за счет тех полей, которые создаются самими телами в случае контакта. Всего различают четыре вида взаимодействия: слабое, сильное, гравитационное, электромагнитное. Сила обозначается буквой F от латинского слова fortis, что в переводе означает сильный.
Что такое модуль силы?
Сила является векторной величиной, это значит, что она обладает, так как направлением, так и модулем. Не так часто встречается случай, когда на тело воздействует одна единственная величина, чаще всего их несколько. В таком случае речь о равнодействующей силы, которая формируется за счет суммирования всех сил, влияющие на тело одновременно. Стоит отметить, что параметр равнодействующая сила является искусственным и создан только для удобства проведения расчетов.
Но что же это модуль силы? Модуль является абсолютной величиной. Это такая величина, которая отражается числом с плюсом во всех случаях. Другими словами характеристики какого-то процесса или явления выражены конкретными числами. Каждая сила характеризуется направлением и величиной, эта величина и есть модуль, вот что это модуль силы.
Модуль равнодействующих двух сил определяется по формулам:
Для модуля равнодействующих нескольких сил все намного сложнее. Для начала надо вводить систему координат, записать и высчитать проекции сил, потом использовать теорему Пифагоры.
Исаак Ньютон внес серьезный вклад в работу над различными видами сил. В связи с этим в качестве единицы измерения силы применяется Н (Ньютон).
Что это модуль скорости?
Каждое тело в процессе перемещения развивает энную скорость, которая характеризуется двумя параметрами: направление и модуль. Что же это модуль скорости? Это число, обозначающее, насколько быстро перемещается тело. Сама скорость является вектором. У нее есть все свойства вектора перемещения, так как выражается посредством него и обладает всеми свойствами данного вектора.
Для определения модуля скорости необходимо учитывать закон движения со всеми своими правилами. Вычисление модуля скорости может осуществляться посредством графика движения. Если недостаточно понятно, что это модуль скорости тела можно использовать одно из понятий: скалярная величина и алгебраическая скорость. Скорость как вектор это величина с направлением и численным значением, при этих условиях модуль скорости тела это не что иное, как длина этого вектора.
Чаще всего речь о прямолинейном движении в рамках координат (x;t). В таком случае для определения данного параметра подойдет формула:
Это значит, что необходимо нужно отнять начальную координату от конечной координаты. Полученный результат нужно разделить на то время, за которое имело место изменение координаты.
Пример определения модуля скорости одного тела относительно другого на основе задачи: два тела перемещаются со скоростью 8 и 6 м/с. Направление их движения перпендикулярное друг другу. Поэтапное решение осуществляется таким образом:
Модуль импульса и модуль оси
Импульс представляет собой векторную величину, чье направление идентично направлению вектора скорости. Он может поменяться только в том случае, если произойдет изменение скорости под воздействием какой-то силы. Но что это модуль импульса и как он рассчитывается? Модуль импульса определяется согласно произведению массы тела на скорость. Его можно легко вычислить, если есть данные по скорости и по массе.
Что это модуль оси? Разъяснение данного понятия, может быть сделана на основе определения понятия ось. Ось представляет собой прямую с заданным направлением. В каком-то роде можно сказать, что это нечто иное, как вектор с величиной модуля, которая тянется к бесконечности. Это и есть модуль оси. Для обозначения оси можно использовать любую букву: t, Z, Y, X и т.д. На ней определяется точка О, известная как начало отсчета. Все расстояния до других точек определяются относительно нее. Для того чтобы сделать проекцию точки на ось, нужно провести перпендикулярную прямую через эту точку на саму ось. В таком случае проекция этой точки, сама точка.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки
Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Основы механики для чайников. Часть 1: Кинематика
В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.
Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.
Траектория, радиус-вектор, закон движения тела
Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.
Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.
Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.
Радиус-вектор – вектор, задающий положение точки в пространстве.
Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.
В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Скорость и ускорение
Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло
А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.
Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.
В системе СИ скорость измеряется в метрах в секунду
Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.
Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости
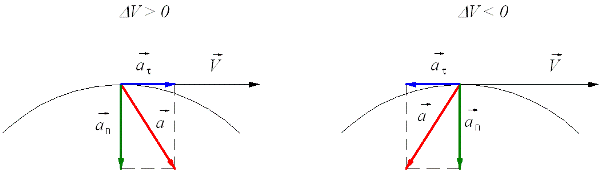
Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.
Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории
Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.
Здесь R – радиус окружности, по которой движется тело.
Закон равноускоренного движения
Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.
Производная по скорости от времени даст значение ускорения a, которое является константой.
Пример решения задачи
Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.
Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.
Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.
Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.
Как вычислить модуль скорости
Скорость тела характеризуется направлением и модулем. Иными словами, модуль скорости – это число, которое показывает, насколько стремительно тело передвигается в пространстве. Перемещение полагает метаморфоза координат.
Инструкция
2. По имеющейся функции зависимости скорости от времени дозволено обнаружить значение скорости в всякий момент времени t. Пускай, скажем, v=2t?+5t-3. Если требуется обнаружить модуль скорости в момент времени t=1, примитивно подставьте это значение в уравнение и посчитайте v: v=2+5-3=4.
3. Когда задача требует обнаружить скорость в исходный момент времени, подставьте в функцию t=0. Таким же образом дозволено обнаружить время, подставив вестимую скорость. Так, в конце пути тело остановилось, то есть, его скорость стала равна нулю. Тогда 2t?+5t-3=0. Отсель t=[-5±?(25+24)]/4=[-5±7]/4. Получается, что либо t=-3, либо t=1/2, а от того что время не может быть негативным, остается только t=1/2.
Модуль числа n представляет собой число единичных отрезков от начала координат до точки n. Причем не главно, в какую сторону будет отсчитываться это расстояние – вправо либо налево от нуля.
Инструкция
2. Помните, что модуль может быть только позитивным числом либо нулем. Модуль позитивного числа равен самому числу. Модуль нуля равен нулю. То есть для всякого числа n, которое огромнее либо равно нулю, будет объективна дальнейшая формула |n| = n. Скажем, |15| = 15, то есть модуль числа 15 равен 15-ти.
Для нахождения метаморфозы скорости определитесь с типом движения тела. В случае если движение тела равномерно, изменение скорости равно нулю. Если тело движется с убыстрением, то изменение его скорости в весь момент времени дозволено узнать, если отнять от мгновенной скорости в данный момент времени его исходную скорость.
Вам понадобится
Инструкция
1. Определение метаморфозы скорости произвольно движущегося по прямой траекторииС поддержкой спидометра либо радара измерьте скорость тела в начале и конце отрезка пути. После этого от финального итога отнимите первоначальный, это и будет изменение скорости тела.
Видео по теме
Для определения скорости разных видов движения потребуются различные формулы. Дабы определить скорость равномерного движения, расстояние поделите на время его прохождения. Среднюю скорость движения находите сложением всех отрезков, которое прошло тело, на всеобщее время движения. При равноускоренном движении узнайте убыстрение, с которым двигалось тело, а при свободном падении высоту, с которой оно предисловие движение.
Вам понадобится
Инструкция
1. Скорость равномерного движения и средняя скоростьИзмерьте расстояние с поддержкой дальномера, которое прошло тело, а время, за которое оно его одолело, с поддержкой секундомера. Позже этого поделите расстояние, пройденное телом на время его прохождения, итогом будет скорость равномерного движения (v=S/t). Если тело движется неравномерно, произведите те же измерения и примените ту же формулу – тогда получите среднюю скорость тела. Это значит, что если бы тело по данному отрезку пути двигалось с полученной скоростью, оно было бы в пути время, равное измеренному. Если тело движется по окружности, измерьте ее радиус и время прохождения полного цикла, после этого радиус умножьте на 6,28 и поделите на время (v=6,28•R/t). Во всех случаях итог получится в метрах в секунду. Для перевода в километры в час помножьте его на 3,6.
2. Скорость равноускоренного движенияИзмерьте убыстрение тела с поддержкой акселерометра либо динамометра, если знаменита масса тела. Секундомером замерьте время движения тела и его исходную скорость, если тело не начинает двигаться из состояния покоя. Если же тело двигается из состояния покоя, она равна нулю. Позже этого узнайте скорость тела, прибавив к исходной скорости произведение убыстрения на время (v=v0+at).
3. Скорость вольно падающего телаС поддержкой дальномера измерьте высоту, с которой падает тело в метрах. Дабы узнать скорость, с которой оно долетит до поверхности Земли (без контроля сопротивления воздуха), умножьте высоту на 2 и на число 9,81 (убыстрение свободного падения). Из итога извлеките квадратный корень. Дабы обнаружить скорость тела на всякий высоте, применяйте ту же методологию, только от исходной высоты, отнимайте нынешнюю и полученное значение подставляйте взамен высоты.
Видео по теме
Человек привык воспринимать представление “скорость ” как что-то больше примитивное, чем это есть на самом деле. Подлинно, проносящийся на перекрестке автомобиль движется с определенной скорость ю, в то время как человек стоит и отслеживает за ним. Но если человек находится в движении, то умнее говорить не об безусловной скорости, а об относительной ее величине. Обнаружить относительную скорость дюже легко.
Инструкция
1. Дозволено продолжить рассмотрение темы движущегося на перекрестка на автомобиле. Человек же, стоя на красном свете светофора, стоит и глядит на проезжающий автомобиль. Человек статичен, следственно примем его за систему отсчета. Система отсчета – такая система, касательно которой движется какое-нибудь тело либо другая физическая точка.
2. Возможен, автомобиль движется со скорость ю 50 км/ч. Но, возможен, что человек побежал следом автомобилю (дозволено, скажем, взамен автомобиля представить маршрутку либо проезжающий мимо автобус). Скорость бега человека 12 км/ч. Таким образом, скорость данного механического транспортного средства представится человеку не столь и стремительной, как было прежде, когда он стоял! В этом каждая и суть относительной скорости. Относительная скорость неизменно измеряется касательно подвижной системы отсчета. Таким образом, скорость автомобиля не будет для пешехода 50 км/ч, а 50 – 12 = 38 км/ч.
3. Дозволено разглядеть еще один живой пример. Довольно припомнить всякий из моментов, когда человек, сидя у окна автобуса, отслеживает за проносящимися мимо автомобилями. Подлинно, из окна автобуса их скорость кажется примитивно потрясающей. И это не изумительно, чай, если принять автобус за систему отсчета, то скорость автомобиля и скорость автобуса надобно будет сложить. Возможен, что автобус движется со скорость ю 50 км/ч, а машины 60 км/ч. Тогда 50 + 60 = 110 км/ч. Именно с такой скорость ю эти самые автомобили проносятся мимо автобуса и пассажиров в нем.Эта же скорость будет объективна и действительна и в том случае, если за систему отсчета принять всякий из проезжающих мимо автобусов автомобилей.
Инструкция
1. Движение тела происходит по некоторой траектории. В случае откровенного движения ею является прямая линия, следственно обнаружить перемещение тела достаточно примитивно: оно равно пройденному пути. В отвратном случае определить его дозволено по координатам исходного и финального расположения в пространстве.
2. Величина перемещения физической точки является векторной, от того что она имеет направление. Следственно, дабы обнаружить ее числовое значение, нужно вычислить модуль вектора, соединяющего точки начала пути и его окончания.
3. Разглядим двухмерное координатное пространство. Пускай тело проделало путь от точки A (x0, y0) до точки B (x, y). Тогда, дабы обнаружить длину вектора АВ, опустите проекции его концов на оси абсцисс и ординат. Геометрически проекции касательно той и иной координатной оси дозволено представить в виде катетов прямоугольного треугольника с длинами:Sx = x – x0;Sy = y – y0, где Sx и Sy – проекции вектора на соответствующих осях.
7. В частном случае откровенного движения тело перемещается только по одной оси, скажем, оси абсцисс. Тогда длина перемещения равна разности финальной и исходной первой координаты точек:S = x – x0.
Вам понадобится
Инструкция
1. Вначале определитесь с типом движения. Если оно равномерное, то довольно измерить длину пути, по которому переместилось тело, сделав это рулеткой, дальномером либо иным доступным методом, и поделить это значение на время, за которое это перемещение осуществлялось. От того что движение равномерное, то модуль скорости на протяжении каждого пути будет идентичен, так что полученная скорость будет равна исходной.
2. При равноускоренном откровенном движении измерьте при помощи акселерометра убыстрение тела, а с подмогой секундомера время его движения, спидометром финальную скорость в конце отрезка пути. Обнаружьте значение модуля исходной скорости, отняв от финальной скорости произведение убыстрения на время движения v0=v-a*t. Если незнакомо значение убыстрения, измеряйте расстояние, которое покрыло тело за время t. Сделайте это при помощи рулетки либо дальномера.
3. Зафиксируйте значение финальной скорости. Обнаружьте исходную скорость, отняв от удвоенного значения расстояния S, поделенного на время, значение финальной скорости v, v0=2S/t-v. Когда значение финальной скорости измерить трудно, а убыстрение знаменито, воспользуйтесь иной формулой. Для этого измеряйте перемещение тела, а также время, которое оно было в пути. От значения перемещения отнимите произведение убыстрения на квадрат времени, поделенное на 2, а итог поделите на время, v0=(S-at?/2)/t либо v0=S/t-at/2.
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки
Всем известно, что скорость материальной точки — это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора — это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему «механика твердых тел». А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
Основываясь на определении скорости, мы можем утверждать, что скорость является вектором. Она непосредственно выражается через вектор-перемещения, отнесенный к промежутку времени, и должна обладать всеми свойствами вектора перемещения.
Направление вектора скорости, так же как направление физически малого вектора перемещения, определяется по чертежу траектории. В этом можно наглядно убедиться на простых примерах.
Если к вращающемуся точильному камню прикоснуться железной пластинкой, то снимаемые им опилки приобретут скорость тех точек камня, к которым прикасалась пластинка, и затем улетят в направлении вектора этой скорости. Все точки камня движутся по окружностям. Во время опыта хорошо видно, что отрывающиеся раскаленные частички-опилки уходят по касательным к этим окружностям, указывая направления векторов скоростей отдельных точек вращающегося точильного камня.
Обратите внимание на то, как расположены выходные трубы у кожуха центробежного водяного насоса или у сепаратора для молока. В этих машинах частицы жидкости заставляют двигаться по окружностям и затем дают им возможность выйти в отверстие, расположенное в направлении вектора той скорости, которую они имеют в момент выхода. Направление вектора скорости в этот момент совпадает с направлением касательной к траектории движения частиц жидкости. И выходная труба тоже направлена по этой касательной.
Точно так же обеспечивают выход частиц в современных ускорителях электронов и протонов при ядерных исследованиях.
Итак, мы убедились, что направление вектора скорости определяется по траектории движения тела. Вектор скорости всегда направлен вдоль касательной к траектории в той точке, через которую проходит движущееся тело.
Для того чтобы определить, в какую сторону вдоль касательной направлен вектор скорости и каков его модуль, нужно обратиться к закону движения. Допустим, что закон движения задан графиком, показанным на рис. 1.54. Возьмем приращение длины пути 



направление движения по траектории, а следовательно, определяет ориентировку вектора скорости вдоль касательной. Очевидно, что через модуль этого приращения длины пути будет определяться модуль скорости.
Таким образом, модуль вектора скорости и ориентировку вектора скорости вдоль касательной к траектории можно определить из соотношения
Здесь 
Итак, мы убедились, что модуль вектора скорости может быть найден по графику закона движения. Отношение 

Еще раз обратим внимание на то, что для полного определения скорости требуется одновременное знание траектории и закона движения. Чертеж траектории позволяет определить направление скорости, а график закона движения — ее модуль и знак.
Если теперь мы обратимся снова к определению механического движения, то убедимся в том, что после введения понятия скорости для полного описания любого движения больше ничего не требуется. Используя понятия радиус-вектора, вектора перемещения, вектора скорости, длины пути, траектории и закона движения, можно получить ответы на все вопросы, связанные с определением особенностей любого движения. Все эти понятия взаимосвязаны друг с другом, причем знание траектории и закона движения позволяет найти любую из этих величин.