На чем основана математика
Математика
Содержание
Основные сведения
Идеализированные свойства исследуемых объектов либо формулируются в виде аксиом, либо перечисляются в определении соответствующих математических объектов. Затем по строгим правилам логического вывода из этих свойств выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Таким образом первоначально, исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.
Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное с математикой положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе было предложено много различных определений математики (см. ниже).
Этимология
В текстах на русском языке слово «математика» или «мафематика» встречается по крайней мере с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год) [5]
Определения
Одно из первых определений предмета математики дал Декарт [6] :
К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики.
Математика… наука о количественных отношениях и пространственных формах действительного мира.
Это определение Энгельса [8] ; правда, далее Колмогоров поясняет, что все использованные термины надо понимать в самом расширенном и абстрактном смысле.
Сущность математики… представляется теперь как учение об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств,— именно тех, которые в качестве аксиом положены в основание теории… Математика есть набор абстрактных форм — математических структур.
Приведём ещё несколько современных определений.
Герман Вейль пессимистически оценил возможность дать общепринятое определение предмета математики:
Вопрос об основаниях математики и о том, что представляет собой в конечном счёте математика, остаётся открытым. Мы не знаем какого-то направления, которое позволит в конце концов найти окончательный ответ на этот вопрос, и можно ли вообще ожидать, что подобный «окончательный» ответ будет когда-нибудь получен и признан всеми математиками.
Разделы математики
1. Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе и образованную дисциплинами:
и высшую математику, изучаемую на нематематических специальностях вузов. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности.
Программа обучения по специальности математика [13] образована следующими учебными дисциплинами:
2. Математика как специальность научных работников Министерством образования и науки Российской Федерации [14] подразделяется на специальности:
3. Для систематизации научных работ используется раздел «Математика» [15] универсальной десятичной классификации (УДК).
4. Американское математическое общество (AMS) выработало свой стандарт для классификации разделов математики. Он называется Mathematics Subject Classification. Этот стандарт периодически обновляется. Текущая версия — это MSC 2010. Предыдущая версия — MSC 2000.
Обозначения
Вследствие того, что математика работает с чрезвычайно разнообразными и довольно сложными структурами, система обозначений также очень сложна. Современная система записи формул сформировалась на основе европейской алгебраической традиции, а также математического анализа (понятия функции, производной и т. д.). Геометрия испокон века пользовалась наглядным (геометрическим же) представлением. В современной математике распространены также сложные графические системы записи (например, коммутативные диаграммы), нередко также применяются обозначения на основе графов.
Краткая история
Академиком А. Н. Колмогоровым предложена такая структура истории математики:
Развитие математики началось вместе с тем, как человек стал использовать абстракции сколько-нибудь высокого уровня. Простая абстракция — числа; осмысление того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, года. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.
Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления. Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами Среднего царства. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля.
Исторически основные математические дисциплины появились под воздействием необходимости вести расчёты в коммерческой сфере, при измерении земель и для предсказания астрономических явлений и, позже, для решения новых физических задач. Каждая из этих сфер играет большую роль в широком развитии математики, заключающемся в изучении структур, пространств и изменений.
Философия математики
Цели и методы
Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного раздела математики — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.
Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.
Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. «Пространство 
, при 
3″ border=»0″ /> является математической выдумкой. Впрочем, весьма гениальной выдумкой, которая помогает математически разбираться в сложных явлениях». [16]
Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.
Основания
Вопрос сущности и оснований математики обсуждался со времён Платона. Начиная с XX века наблюдается сравнительное согласие в вопросе, что надлежит считать строгим математическим доказательством, однако отсутствует согласие в понимании того, что в математике считать изначально истинным. Отсюда вытекают разногласия как в вопросах аксиоматики и взаимосвязи отраслей математики, так и в выборе логических систем, которыми следует при доказательствах пользоваться.
Помимо скептического, известны нижеперечисленные подходы к данному вопросу.
Теоретико-множественный подход
Предлагается рассматривать все математические объекты в рамках теории множеств, чаще всего с аксиоматикой Цермело — Френкеля (хотя существует множество других, равносильных ей). Данный подход считается с середины XX века преобладающим, однако в действительности большинство математических работ не ставят задач перевести свои утверждения строго на язык теории множеств, а оперируют понятиями и фактами, установленными в некоторых областях математики. Таким образом, если в теории множеств будет обнаружено противоречие, это не повлечёт за собой обесценивание большинства результатов.
Логицизм
Данный подход предполагает строгую типизацию математических объектов. Многие парадоксы, избегаемые в теории множеств лишь путём специальных уловок, оказываются невозможными в принципе.
Формализм
Данный подход предполагает изучение формальных систем на основе классической логики.
Интуиционизм
Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства (но, как считается, и более надёжную). Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств — бессмысленными (неформализуемыми).
Конструктивная математика
Основные темы
Числа
Понятие «число» первоначально относилось к натуральным числам. В дальнейшем оно было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.
| |||||||||||||||
 |  | ||||||||||||||
| Комплексные числа | Кватернионы | ||||||||||||||
 Числовые системы | |
|---|---|
| Счётные множества | Натуральные числа ( ) • Целые ( ) • Рациональные ( ) • Алгебраические ( ) • Периоды • Вычислимые • Арифметические |
| Вещественные числа и их расширения | Вещественные ( ) • Комплексные ( ) • Кватернионы ( ) • Числа Кэли (октавы, октонионы) ( ) • Седенионы ( ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) |
| Другие числовые системы | Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа |
| См. также | Двойные числа • Иррациональные числа • Трансцендентные • Числовой луч • Бикватернион |
Преобразования
 |  |  |  |
| Арифметика | Дифференциальное и интегральное исчисление | Векторный анализ | Анализ |
 |  |  | |
| Дифференциальные уравнения | Динамические системы | Теория хаоса |
Структуры
Пространственные отношения
Более наглядные подходы в математике.
Дискретная математика
Дискретная математика включает средства, которые применяются над объектами, способными принимать только отдельные, не непрерывные значения.
 |  |  |  |
| Математическая логика | Теория вычислимости | Криптография | Теория графов |
Коды в системах классификации знаний
Онлайновые сервисы
Существует большое число сайтов, предоставляющих сервис для математических расчётов. Большинство из них англоязычные. [20] Из русскоязычных можно отметить сервис математических запросов поисковой системы Nigma.
Что такое математика
Математика — царица всех наук
Гаусс Карл Фридрих
Математика — наука, исторически основанная на решении задач о количественных и пространственных соотношениях реального мира путём идеализации необходимых для этого свойств объектов и формализации этих задач. Наука, занимающаяся изучением чисел, структур, пространств и преобразований.
Как правило, люди думают, что математика — это всего лишь арифметика, то есть изучение чисел и действий с их помощью, например, умножения и деления. На самом деле математика — это намного больше. Это способ описать мир и то, как одна его часть сочетается с другой. Взаимоотношения чисел выражаются в математических символах, которые описывают Вселенную, в которой мы живем. Любой нормальный ребенок может преуспевать в математике, потому что «ощущение числа» — это врожденная способность. Правда, для этого нужно приложить некоторые усилия и затратить немного времени.
Умение считать — это еще не все. Ребенку необходимо уметь хорошо выражать свои мысли, чтобы понимать задачи и устанавливать связи между фактами, которые хранятся в памяти. Для того чтобы выучить таблицу умножения, нужны память и речь. Именно поэтому некоторым людям с поврежденным мозгом трудно умножать, хотя другие виды счета не представляют для них сложности.
Для того чтобы хорошо знать геометрию и разбираться в форме и пространстве, требуются и другие виды мышления. С помощью математики мы решаем в жизни проблемы, например, делим шоколадку поровну или находим нужный размер ботинок. Благодаря знанию математики ребенок умеет копить карманные деньги и понимает, что можно купить и сколько денег тогда у него останется. Математика — это еще и способность отсчитать нужное количество семян и посеять их в горшочек, отмерять нужное количество муки для пирога или ткани на платье, понять счет футбольной игры и множество других повседневных дел. Везде: в банке, в магазине, дома, на работе — нам необходимо умение понимать числа, формы и меры и обращаться с ними. Числа — это только часть особого математического языка, а лучший способ выучить любой язык — это применять его. И начинать лучше с ранних лет.
О математике «умно»
Обычно идеализированные свойства исследуемых объектов и процессов формулируются в виде аксиом, затем по строгим правилам логического вывода из них выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Т.о. первоначально исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.
Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное к математике положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе существует много различных определений математики.
Разделы математики
Цели и методы
Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного математика — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.
Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.
Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.
Видео-лекция Смирнова С.К. и Ященко И.В. «Что такое математика»:
Прикладная или фундаментальная: какой считают в мире математику
Можно ли считать математику фундаментальной наукой или это всего лишь инструмент, как писал советский математик Колмогоров, на службе у естественных наук — этот вопрос остается открытым. Даже сами математики отказываются однозначно отвечать на него. Методист по математике Университета Иннополис Дмитрий Бебчук рассказал на фестивале науки и технологии «ПРОСТО», организованном российским ИТ-вузом, о том, какие изобретения человечества были бы невозможны без математики и почему математизирование — это процесс творческий, не требующий никаких практических целей.
Читайте «Хайтек» в
Наука о структурах или просто расчеты?
« Британника» говорит, что математика — это наука о структурах, порядках и отношениях, возникшая из элементарных практик подсчета, измерения и описания форм объектов. Она строится на логических рассуждениях и количественных расчетах. Группа французских математиков, которые взяли себе в 1935 году коллективный псевдоним Никола Бурбаки, предложила такое определение: математика — это наука об отношениях между объектами, о которых ничего не известно, кроме их свойств. именно ими объекты и описываются. Может возникнуть двоякое впечатление. С одной стороны, у нас есть конструктивное определение математики, а с другой, математика — это когда «взяли что-то и посчитали». Этот своеобразный конфликт выразился в том числе в установлении теории множеств. Есть аксиоматика Сернела Френкеля, которая являет собой конструктивный подход к теории множеств, но существуют и альтернативы. Это всё возникло из-за парадокса Рассела.
Парадокс Рассела — открытый в 1901 году Бертраном Расселом теоретико-множественный парадокс (антиномия), демонстрирующий противоречивость логической системы Фреге, являвшейся ранней попыткой формализации наивной теории множеств Георга Кантора.
Парадокс можно описать следующим образом. Условимся называть множество «обычным», если оно не является своим собственным элементом. Например, множество всех людей является «обычным», так как само множество — не человек. Примером «необычного» множества является множество всех множеств, так как оно само является множеством, а, следовательно, само является собственным элементом.
Система аксиом Цермело — Френкеля (ZF) — наиболее широко используемый вариант аксиоматической теории множеств. Сформулирована Эрнстом Цермело в 1908 году для преодоления парадоксов теории множеств, а затем была уточнена Абрахамом Френкелем в 1921 году. Система аксиом записана на языке логики первого порядка.
Я попытаюсь вам доказать, что математика — это фундаментальная наука. Фундаментальная наука должна обладать следующими свойствами: ее результаты должны быть универсальны; в ее задачи не должна входить изначально практическая реализация полученных результатов; и она позволяет нам получать новые знания о природе, то есть иметь предсказательную силу.
В универсальности результатов математики сомнений нет. Это самый легкий пункт, поэтому он стоит первым. Действительно, даже на уровне «дважды два — четыре»: в любое время и на любом континенте это будет, конечно же, четыре.
Как из чистых идей родились практические инструменты
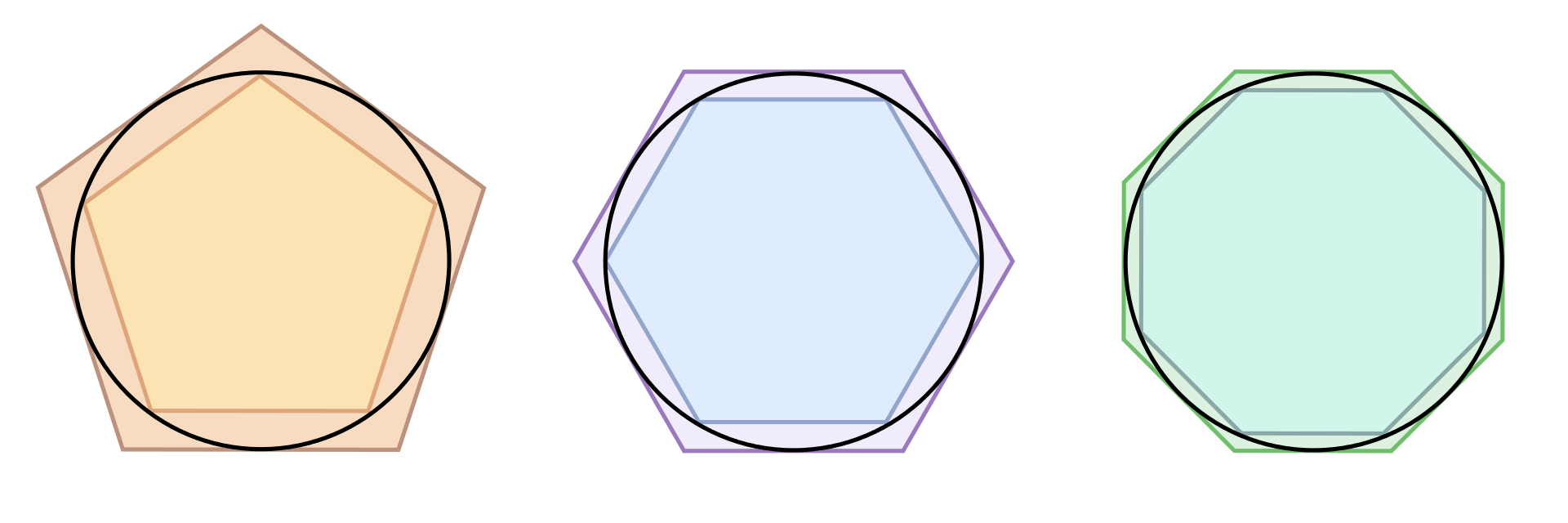
Существуют четыре области математики, которые развились из совершенно абстрактной идеи. Во-первых, анализ бесконечно малых, то, что сейчас называют математическим анализом. Началось всё с того, что предположительно Антифон в V веке до нашей эры предложил метод исчерпывания. Он и сейчас так называется. С помощью этого метода можно находить площадь фигур, границы которых — не отрезки. Например, площадь круга. Если есть круг, то его можно заключить, например, в пятиугольник, а также вписать в него пятиугольник. Площадь круга получится чем-то средним между ними. Если заменить пятиугольник на шести-, семи- и восьмиугольник, то точность приближения возрастет. Чем больше количество сторон у нашего вот многоугольника, который вписан и описан около круга, тем лучше оказывается наше приближение.
Но площадь круга пропорциональна квадрату радиуса, а коэффициент пропорциональности — это какое-то число. Были предложены оценки этого числа: например, Архимед предположил, что это примерно 22/7, эта оценка позволяет нам получить точность до двух знаков после десятичной запятой. А пресловутый Цзу Чунжи уже предложил оценку намного лучше: 355/113, уже шесть знаков после запятой. В конце концов, было доказано, что пи — это число иррациональное и даже трансцендентное, то есть не является алгебраическим числом.
Цзу Чунжи — китайский математик и астроном. Как астроном определил сидерические периоды обращения планет Солнечной системы с высокой точностью. Разработал новый календарь с учетом явления прецессии. Как математик первым в мире рассчитал число пи с точностью до седьмого знака после запятой, дав его значение между 3,1415926 и 3,1415927; более точное значение было вычислено лишь тысячу лет спустя.
Принцип Кавальери очень прост: если у вас есть два объемных тела одинаковой высоты и на каждом уровне площади иссечений одинаковы, то и объемы этих тел одинаковы. Такой принцип подходит для нахождения объемов тел, у которых грани необязательно плоские. Например, конус. Из таких совершенно теоретических подходов к XVII веку уже развивается дифференциальное и интегральное исчисление, у истоков которого стоят двое ученых — Ньютон и Лейбниц, которые примерно одновременно развивали эту область. Практическое применение их работ сегодня: поиск длины кривой и касательной к сфере, дивергенции, роторы и даже двумерное нормальное распределение, благодаря которому можно искать вероятности сложноконструируемых событий.
Бонавентура Кавальери — итальянский математик, предтеча математического анализа, наиболее яркий и влиятельный представитель «геометрии неделимых». Выдвинутые им принципы и методы позволили еще до открытия математического анализа успешно решить множество задач аналитического характера.
В XVI веке Джероламо Кардано ввел понятие комплексного числа. В его трудах комплексные числа описаны как совершенно утонченные и бесполезные структуры, утонченные — это позитивная характеристика, а бесполезные — ну мы понимаем. Он не видел им совершенно никакого применения, но, тем не менее, пытался развивать эту теорию. Уже потом стало ясно, что это полезный инструмент для многих областей. Альберт Эйнштейн согласился бы. В качестве примеров — расчёт электрических цепей переменного тока, который делается гораздо проще с применением комплексно-значимых функций. Всяческие теоремы о распределении простых чисел — небезызвестная дзета-функция Римана и теорема, связанная с ней, гипотеза, на самом деле, потому что она еще не доказана — это одна из семи проблем тысячелетия. Гиперкомплексные числа, так называемые кватернионы, нашли свое применение в позиционировании. Тут меня поймут робототехники. Когда мы определяем или задаем положение трехмерного объекта в пространстве, то кватернионы исключительно полезны. А обойтись без выхода в это гиперкомплексное пространство нам уже тяжелее.
Джероламо Кардано — итальянский математик, инженер, философ, врач и астролог. В его честь названы открытые Сципионом дель Ферро формулы решения кубического уравнения (Кардано был их первым публикатором), карданов подвес, карданный вал и решетка Кардано.
Кватернионы — система гиперкомплексных чисел, образующая векторное пространство размерностью четыре над полем вещественных чисел. Предложены Уильямом Гамильтоном в 1843 году.
Некоторые алгоритмы шифрования основаны на свойствах эллиптических кривых, а, точнее, на их алгебраических свойствах. Но всё началось с того, что Диофант Александрийский в III веке нашей эры пытался найти решение этого уравнения: y*(6-y)=x3-x. В конце XVII — начале XVIII века Ньютон тоже пытался его решить. Все вылилось в целую теорию, которая позволяет нам достаточно быстро зашифровать данные, с тем, чтобы их расшифровка требовала существенно больше времени. То есть мы получаем криптографически такой механизм — алгоритм.
Задачу мостов Эйлера: существует ли маршрут, чтобы обойти каждый мост Кенигсберга только по одному разу, — сегодня может решить почти любой олимпиадник. Этот вопрос XVIII века, тогда еще практически неприменимый, породил целую область математики — топологию. Сегодня она применяется, например, в робототехнике. У манипулятора есть конфигурационное пространство. Например, у двухзвенного манипулятора — это тор. Но тор — это определенный топологический объект: если мы возьмем две точки на торе, то сможем сказать про траекторию передвижения между этими двумя точками, про минимальность и так далее. То есть появляется целая область для анализа. А если манипулятор трехзвенный, то и поверхность становится значительно сложнее, а задача по нахождению какого-то оптимального пути или даже просто нахождению пути — на порядки. Тут без топологии уже не обойтись.
Анализ бесконечно малых, топология, эллиптические кривые — все это доказывает то, что в развитие этих областей было вовлечено много людей. А после XVIII века математика уже становится профессиональный наукой, то есть человек со стороны практически не имеет шансов добиться в ней значимых на мировом уровне успехов. Второй тезис, получается, доказан. Эти люди занимались математикой всю жизнь, не надеясь на то, что их конкретные результаты будут практически применимыми.
Как способ описать природу
Пресловутый Бозон Хиггса, который, конечно, прежде чем был обнаружен и зафиксирован, сначала был рассчитан. То есть была целая теория, основанная на расчетах. Теория, согласно которой такая частица должна существовать и должна обладать определенными свойствами. Это доказывает, что математика позволяет получать новые знания о природе. Вернемся к самому началу: что математика — это наука о неких структурах, у которых мы знаем только свойства, а потом уже смотрим, а что же из этого получается. Бозон Хиггса, который тогда еще не знали, но уже по предположениям ученых должен был обладать определенными свойствами.
Второй пример — девятая планета. Российский ученый Батыгин, который сейчас преподает в США, сначала вычислил орбиту девятой планеты, прежде чем ее обнаружили. То есть, согласно каким-то расчетам, эта планета должна была существовать, а потом она уже была обнаружена в расчетной точке.
Получается, что математика — фундаментальная наука. Но многие скажут, что математика — это просто дисциплина на службе естественных наук, и отчасти они будут правы. И с ними согласился бы даже Колмогоров, который в предисловии к книге Куранта и Роббинса так и сказал, что математика неотделима от ее практических применений.
Андрей Колмогоров — советский математик, один из основоположников современной теории вероятностей, им получены фундаментальные результаты в топологии, геометрии, математической логике, классической механике, теории турбулентности, теории сложности алгоритмов, теории информации, теории функций и в ряде других областей математики и ее приложений.
Рихард Курант — немецкий и американский математик, педагог и научный организатор. Известен как автор классической популярной книги по математике «Что такое математика?», а также как один из авторов критерия Куранта — Фридрихса — Леви.
Герберт Роббинс — американский математик и статистик. Его именем названы лемма Роббинса, алгебра Роббинса, теорема Роббинса и другие термины.
Вейль говорит о том, что вопрос об основаниях математики и о том, что в конечном счете она собой представляет, остается открытым. И неизвестно такого направления, которое позволит в конце концов найти окончательный ответ на этот вопрос. Можно ли ожидать, что он когда-нибудь будет получен и признан всеми математиками? Вейль указывает на то, что сам процесс изучения математики, математизирование — это творческий процесс, когда люди, не надеясь на практическое применение их результатов, результатов их работы, просто занимаются этим процессом. Но а то, что он описывает мир, надеюсь, я вас убедил, тут сомнений уже нет. Математика действительно описывает мир, и нет естественной науки, которая не пользовалась бы математическим аппаратом. В современном мире и общественные науки, в том числе социология, пользуются математическими методами как методами для исследования.
Андре Вейль — французский математик, внесший значительный вклад в алгебраическую геометрию и топологию, член группы Бурбаки. Важнейшие труды в области алгебраической геометрии, которую сумел обосновать с нужным уровнем строгости, получил важные результаты в функциональном анализе, в частности в теории меры и интегрирования в топологических группах и теории чисел, к которой применил аппарат гомологической алгебры и функционального анализа.