На что делится градус
Градусная мера угла
Градус — угол, равный 1/180 части развернутого угла. Градусная мера
угла — это положительное число, показывающее сколько раз градус и его части
укладываются в данном угле. Углы измеряют с помощью транспортира.
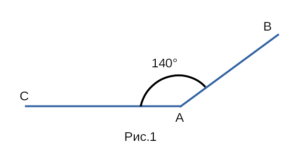
На рисунке 1 изображен ∠СAB. Градусная мера
которого равна 140°. Обычно записывают кратко: ∠СAB=140°.
Названия определённых частей градуса:
Минута — это 1/60 часть градуса. Секунда — это 1/60 часть минуты.
Минуту обозначают знаком ′, а секунду знаком ″.
Например, угол 45 градусов, 30 минут, 15 секунд обозначают вот так: 45°30′15″.
Равные углы имеют равные градусные меры. Меньший угол имеет меньшую градусную меру.
Мы знаем, что градус составляет 1/180 часть развернутого угла, из этого мы можем сделать вывод, что
развернутый угол равен 180°. Мы также знаем, что неразвернутый угол меньше развернутого угла,
поэтому неразвернутый угол меньше 180 градусов.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
Пример на рисунке 2 — ∠CAH + ∠BAH = ∠CAB ⇒ 60° + 120° = 180°.
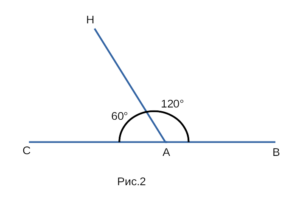
Углы называют не только развернутыми и неразвернутыми, но и еще называют
прямыми, острыми и тупыми. Прямым называется угол равный 90°. Острым называется
угол меньше 90°. Тупым называется угол больше 90°, но меньше 180°.
Углы и градусы
Определение величин углов
Первые попытки древних людей измерять земельные участки
(изначально геометрия – это измерение земли) наткнулись на
острую необходимость в угловых измерениях. Крайне редко
их наделы имели правильную форму. Поэтому понятие угла
появилось практически одновременно с линейным отрезком
и/или расстоянием. Другое дело, измерять и тем более
вычислять значения углов люди научились значительно позже.
Хотя уже древние греки оперировали этими понятиями более чем успешно.
Полупрямая (луч) в геометрии определяется как бесконечно длинная
прямая, имеющая начало. Она состоит из всего множества точек,
лежащих на этой линии, включая начальную. Угол же образуют два
луча с совмещенными точками начала. Можно дать и такое
определение этой геометрической фигуры. Причем общую для лучей
точку принято называть вершиной угла, а лучи – сторонами угла.
Удивительно, но размещение точки в любом месте любой прямой
эквивалентно получению двух равновеликих и разнонаправленных
лучей с общим началом. Следовательно, эта нехитрая операция
создает угол как геометрическую фигуру.
Откуда взялся градус
Достоверное происхождение этой угловой меры неизвестно.
Наиболее вероятная гипотеза о делении на 60 частей
угла равностороннего треугольника вавилонянами отлично
согласуется с шести десятеричной системой счисления, принятой
в этом архаичном обществе. Число 60 делится на 2, 3, 5, 6, 10,
15, 30 и, собственно, на 60. Отсюда удобство его применения в
торговле и прочих бытовых отношениях.
Согласно другой версии, окружность разделили на 360 равных
фрагментов по причине равенства их количества числу дней в году.
Персы, например, немало повлиявшие на развитие математики в
целом и геометрии в частности, использовали именно такой календарь.
В любом случае градус используется до сих пор, обозначая 1/360 часть
полного оборота (делит круг на 360 равных секторов). Само слово с
латыни переводится как шаг, ступень, порог. Отсюда слово градуировка,
применимое абсолютно ко всем измерительным приборам.
Для измерения более мелких величин углов используют минуту
и секунду. Эти величины также являются результатом дробления
на 60. Минута делит градус, а секунда минуту. То есть 1 минута
равна 1/60 градуса, а секунда составляет 1/60 минуты или 1/3600 градуса.
Транспортир, знакомый каждому со школьных времен – элементарнейший
инструмент, позволяющий довольно точно измерять или рисовать углы.
Разумеется, в практике промышленности, строительства и других сферах
человеческой деятельности применяются более точные средства,
теодолит, как вариант. Но результат измерения любого современного
инструмента всегда выражается в градусах.
Учитывая простоту фигуры и ее составляющих, углы не отличаются
большим разнообразием. Принято выделять следующие их виды:
Помимо прямого, существует еще несколько частных случаев, а именно:
Геометрия, оставаясь неотъемлемой частью математики,
все же выделена в отдельную дисциплину. Причина
такого подразделения проста. Математическая наука
не терпит даже тени хаоса, что выражается в четкой
классификации ее разделов, но с сохранением
органической связи между собой.
На самом деле, без глубокого знания основ геометрии
практически невозможно изучить смежные математические
дисциплины, такие как тригонометрия, анализ, интегральное
или дифференциальное счисления. Более того, изучение
любой точной науки требует свободного владения
геометрическими понятиями. Механика или оптика
в физике – наиболее яркое тому подтверждение.