На что основывается источник информации типа экстраполяция существующих тенденций
Социально-экономическое прогнозирование методом экстраполяции
Экстраполяция как один из важнейших способов современного социально-экономического и политического прогнозирования. Тренд – изменение, определяющее общее направление развития, основную тенденцию временных рядов. Сущность метода наименьших квадратов.
| Рубрика | Экономико-математическое моделирование |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 02.02.2018 |
| Размер файла | 21,2 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru
Размещено на http://www.allbest.ru
В настоящее время ни одна сфера жизни общества не может обойтись без прогнозов как средства познания будущего. Особенно важное значение имеют прогнозы социально-экономического развития общества, обоснование основных направлений экономической политики, предвидение последствий принимаемых решений. Социально-экономическое прогнозирование является одним из решающих научных факторов формирования стратегии и тактики общественного развития.
Актуальность данной темы как в условиях развитой рыночной экономики, так и переходной экономики определяется тем, что уровень прогнозирования процессов общественного развития обуславливает эффективность планирования и управления экономикой и другими сферами.
Целью данной курсовой работы является рассмотрение методологии и методик разработки социально экономических прогнозов для определения сущности, областей применения и наиболее эффективных методов прогнозирования. Для этого необходимо решить следующие задачи: определить сущность методов социально-экономического прогнозирования и области их применения в ходе изучения теоретико-методологических основ методологии прогнозирования; дать характеристику методов социально-экономического прогнозирования в экономически развитых странах и выявить особенности их применения в современной Украине.
В процессе написания данной курсовой работы были использованы учебники под редакцией В.О. Мосина, К.Л. Трисеева, В. Цыгичко, В.В. Денискина, а также научные статьи по исследуемой проблеме в периодических изданиях «США: экономика политика идеология», «Мировая экономика и международные отношения», «Проблемы прогнозирования», «Российский экономический журнал», «Проблемы прогнозирования», «Российский экономический журнал», «Экономика Украины», «Вестник МГУ».
Формализованные методы делятся по общему принципу действия на четыре группы: экстраполяционные (статистические), системно-структурные, ассоциативные и методы опережающей информации.
В практике прогнозирования экономических процессов преобладающими, по крайней мере до последнего времени, являются статистические методы. Это вызвано, главным образом, тем, что статистические методы опираются на аппарат анализа, развитие и практика применения которого имеют достаточно длительную историю.
Рассмотрим методы экстраполяции, являющиеся одними из наиболее распространенных методов прогнозирования.
Для целей краткосрочного прогнозирования также может использоваться метод экспоненциального сглаживания. Средний уровень ряда на момент t равен линейной комбинации фактического уровня для этого же момента и среднего уровня прошлых и текущего наблюдений.
Экстраполяция тренда возможна, если найдена зависимость уровней ряда от фактора времени t.
Модель стационарного процесса, выражающая значение показателя yt в виде линейной комбинации конечного числа предшествующих значений этого показателя и аддитивной случайной составляющей, называется моделью авторегрессии.
1. Понятие социально-экономического прогнозирования
Как отмечает Антохонова И.В., отличительная особенность прогнозирования состоит в том, что оно обосновывает возникновение таких процессов и форм материальной и духовной жизни общества, которые в данный момент недоступны непосредственному восприятию, а также проверке на практике.
Социально-экономическое прогнозирование основывается на достижениях науки в области познания закономерностей развития общества, выяснения тенденций социально-экономического и технологического прогресса.
У прогнозируемых социальных объектов интенсивность взаимосвязи предвидения и управления может быть настолько высокой, что может изменить предсказанное состояние путем предпринятых действий на основе управленческих решений. Иными словами, управленческие решения приводят к “самоосуществлению” или к “саморазрушению” прогноза. В прогностике это называется “эффектом Эдипа”.
Прогнозирование тесно связано со статистикой и во многом базируется на статистических данных и методах исследования массовых явлений.
Особое значение в настоящее время имеет прикладная статистика, адаптирующая методы многомерного статистического анализа к решению социально-экономических задач. При этом решаются следующие задачи: типологизация (классификация) или выявление однородных в определенном смысле классов; снижение размерности исследуемого пространства данных и восстановление (прогноз) значений зависимых показателей по значениям определенного набора независимых признаков.
Таким образом, приведенные дисциплины тесно связаны между собой, существенным моментом является обязательная методологическая составляющая в виде экономической теории.
2. Метод экстраполяции
Экстраполяция широко применяется в демографии при расчетах будущей численности населения, его половозрастной и семейной структур и т. д. С помощью этого метода может быть рассчитано будущее омоложение или старение населения, дана характеристика рождаемости, смертности, брачности в периоды, которые отстоят от настоящего на несколько десятилетий.
С помощью компьютерных программ (Exel и др.) можно построить экстраполяцию в виде графика в соответствии с имеющимися формулами.
Однако в социальном прогнозировании возможности экстраполяции как метода прогнозирования в некотором роде ограничены. Это вызвано рядом причин, которые связаны с тем, что социальные процессы развиваются во времени. Это ограничивает возможности их точного моделирования. Так, до какого-то момента процесс может медленно нарастать, а затем наступает период бурного развития, который завершается этапом насыщения. После этого процесс опять стабилизируется. Если не учесть подобные особенности протекания социальных процессов, то применение метода экстраполяции может привести к ошибке.
Формализованные методы прогнозирования базируются на математической теории, которая обеспечивает повышение достоверности и точности прогнозов, значительно сокращает сроки их выполнения, позволяет облегчить деятельность по обработке информации и оценке результатов. В состав формализованных методов прогнозирования входят: методы экстраполяции и методы математического моделирования.
Задача прогноза состоит в определении вида экстраполирующих функций на основе исходных эмпирических данных и параметров выбранной функции. Первым этапом является выбор оптимального вида функции, дающей наилучшее описание тренда. Следующим этапом является расчет параметров выбранной экстраполяционной функции. При оценке параметров зависимости наиболее распространенными являются метод наименьших квадратов и его модификаций, метод экспоненциального сглаживания, метод скользящей средней и др.
Сущность метода наименьших квадратов состоит в минимизации суммы квадратических отклонений между наблюдаемыми и расчетными величинами. Данный метод широко применяется в прогнозировании в силу его простоты и возможности реализации на ЭВМ. Недостаток метода состоит в том, что модель тренда жестко фиксируется, а это делает возможным его применение только при небольших периодах упреждения, т.е. при краткосрочном прогнозировании.
Метод экспоненциального сглаживания дает возможность получить оценки параметров тренда, характеризующих не средний уровень процесса, а тенденцию, сложившуюся к моменту последнего наблюдения. Данный метод применяется при кратко- и среднесрочном прогнозировании. Его преимущества состоят в том, что он не требует обширной информационной базы и предполагает ее интенсивный анализ с точки зрения информационной ценности различных членов временной последовательности. Модели, описывающие динамику показателя, имеют простую математическую формулировку, а адаптивная эволюция параметров позволяет отразить неоднородность и текучесть свойств временного ряда.
Метод скользящей средней дает возможность выравнивать динамический ряд путем его расчленения на равные части с обязательным совпадением в каждой из них сумм модельных и эмпирических значений.
Метод экстраполяции заключается в приложении определенной для базисного периода тенденции развития экономического процесса к прогнозируемому периоду, он основывается на сохранении в будущем сложившихся условий развития процесса. При использовании этого метода необходимо иметь информацию об устойчивости тенденций развития объекта за срок, в 2-3 раза превышающий срок прогнозирования. Длительная тенденция изменения экономических показателей называется трендом. Последовательность действий при экстраполировании:
· четкое определение задачи, выдвижение гипотез о возможном развитии прогнозируемого объекта, рассмотрение факторов, стимулирующих или препятствующих развитию данного объекта, определение необходимой экстраполяции и ее допустимой дальности;
· выбор системы параметров, унификация различных единиц измерения, относящихся к каждому параметру в отдельности;
· сбор и систематизация данных, проверка их однородности и сопоставимости;
· выявление тенденций или симптомов изменения изучаемых величин в ходе статистического анализа и непосредственной экстраполяции данных.
Операцию экстраполяции в общей форме можно представить в виде определения значения функции:
При экстраполировании используются методы: наименьших квадратов и его модификации; экспоненциального сглаживания, скользящей средней и др.
экстраполяция экономический тренд
Пример экстраполяции: ряд чисел 1, 4, 9, 16 подсказывает, что следующим числом будет 25, поскольку начало ряда составляют квадраты чисел 1, 2, 3, 4. Мы экстраполировали найденный принцип на ненаписанную часть ряда. Наиболее простым и известным является метод на основе средней, самая простая экстраполяция:
Метод экстраполяции
Добавлено в закладки: 0
М етод экстраполяции – это один из главных способов прогноза, который основывается на прогнозировании событий, учитывая анализ показателей, которые имели место в прошлые годы (при этом, не меньше чем за 5 – 8 лет). В данный момент есть приблизительно триста уравнений, которые дают возможность определить тенденции процессов и позволяют оценить линейную простую зависимость явления и квадратичную зависимость.
Экстраполи́рование, экстраполя́ция, (от лат. extrā — снаружи, вне, кроме, за и лат. polire — выправляю, приглаживаю, меняю, изменяю) — это особенный вид аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не меж фиксированными значениями.
Другими словами, экстраполяция — это приближённое определение значений функции в точках, которые лежат вне отрезка, по её значениям в точках.
Методы
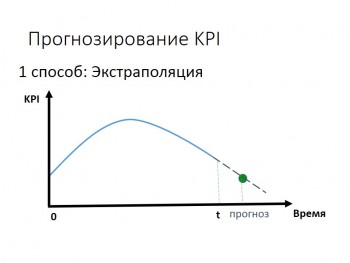
Самый распространённый способ экстраполяции — это параболическая экстраполяция, при которой в точке берётся значение многочлена степени, которая принимает в точке заданные значения. Для параболической экстраполяции применяют интерполяционные формулы.
Применение
Общее значение — это распространение выводов, которые получены из наблюдения над одной частью явления, на его другую часть.
В маркетинге — это распространение выявленных закономерностей развития изучаемого предмета на будущее.
В статистике — это распространение тенденций, установленных в прошлом, на будущий период (экстраполяция во времени используется для перспективных расчетов населения); распространение выборочных данных на прочую часть совокупности, которая не подвергнута наблюдению (экстраполяция в пространстве).
Одним из более распространенных способов краткосрочного прогнозирования экономических явлений — это экстраполяция
Термин “экстраполяция” имеет немного толкований в широком смысле экстраполяция – это способ научного исследования, который заключается в распространении выводов, которые получены из наблюдений за одной частью явления, на а другую его часть В узком смысле – это определение по нескольким данным функции прочих ее значений вне данного ряда за этим рядом.
Прогноз экстраполяции
Экстраполяция заключена в изучении сложившихся в настоящем и прошлом устойчивых тенденций экономического развития и их перенос на будущее
Цель данного прогноза — это показать, к каким итогам можно сделать в будущем, когда передвигаться к нему с аналогичной ускорением или скоростью, что и в прошлом

В прогнозировании экстраполяция используется при изучении временных рядов экстраполяции в общем типе можно представить, как определенное значение функции зависимо от особенностей изменения уровней в рядах динамики способы экстраполяции могут быть сложными и простыми.
Простые способы экстраполяции базируются на предположении относительной устойчивости в будущем абсолютных значений уровней, среднего абсолютного прироста, среднего уровня ряда, среднего темпа роста.
Различные способы экстраполяции
Рассмотрим дет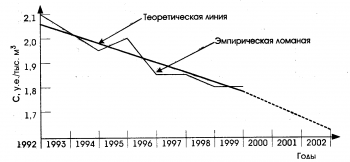
При экстраполяции на основании среднего уровня ряда применяется принцип, при котором прогнозируемый уровень равняется среднему значению в прошлом уровней ряда.
В данной ситуации экстраполяция дает точечную прогностическую оценку. Точное совпадение данных оценок с фактическими данными — маловероятное явление. Таким образом, прогноз обязан быть в виде интервала значений.
Полученный доверительный интервал учитывает неопределенность, которая связана с оценкой средней величины, и его использование для прогнозирования увеличивает степень надежности прогноза. Однако недостаток рассматриваемого подходов периода — это то, что доверительный интервал не связывается с периодом предупреждения.
Экстраполяцию по среднему абсолютному приросту можно провести тогда, когда линейной считать общую тенденцию развития явления.
Чтобы рассчитать прогнозное значение, уровень необходимо определить абсолютный средний прирост. Затем, зная уровень ряда динамики, который принимают за основу экстраполяции.
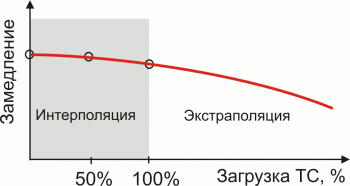
Доверительный интервал прогноза по средним темпом роста можно определить лишь в том случае, когда средний темп роста рассчитывают при помощи статистического оценивания параметров экспоненциальной кривой.
Все три рассмотренные способа экстраполяции тренда простейшие, но вместе и самые приближенные.
Сложные способы экстраполяции предусматривают выявление главной тенденции, то есть использование статистических формул, которые описывают тренд.
Способы данной группы возможно разделить на два главных вида: адаптивные и аналитические (кривые роста).
Аналитические способы прогнозирования
В основание аналитических способов прогнозирования (кривых роста) лежит принцип получения при помощи метода самых малых квадратов оценки детерминированной компоненты, которая характеризует главную тенденцию
Адаптивные способы прогнозирования основываются на том, что процесс реализации их заключен в вычислении последовательных во времени значений прогнозируемого показателя, учитывая степень влияния прошлых уровней. К ним относят способы экспоненциальной и текучей средних, способ гармонических весов, способ авторегрессииї.
Способ аналитического выравнивания тренда (способ наименьших квадратов) может быть использован лишь тогда, когда развитие явления довольно хорошо описывают построенную модель и условия, которые определяют тенденцию развития в прошлом, не изменятся существенно в будущем. При выполнении данных требований прогнозирование производится при помощи подстановки в уравнение тренда значений независимой переменной знает величине периода предупреждения.
Процедура создания прогноза по применению аналитического выравнивания тренда включает в себя такие этапы:
1) выбор формы кривой, которая отображает тенденцию;
2) определение показателей, характеризующие количественно тенденции изменений;
3) оценка вероятности прогнозных расчетов
Подбор формы кривой возможно осуществлять на основании построения графика, суммарный тип которого обычно дает возможность установить:
а) имеет динамический ряд показателя выраженную четко тенденцию;
б) если так, то данная тенденция плавная;
в) каков характер тенденции
Отвечая на данные вопросы, нужно помнить, что наружная простота графика ложная. Каждая динамическая задача намного сложнее от статического и каждая точка кривой — это результат изменения явления во времени и пространстве.
Ввиду этого для увеличения достоверности и обоснованности выравнивания для более точного выявления тенденции, которая есть, нужно провести вариантный расчет по некоторым аналитическими функциями и на основании статистических и экспертных оценок определить лучшую форму связей.
На втором этапе нужно определить параметры уравнения связи. Для того, чтобы их найти, применяют способ малых квадратов. В данной ситуации выравнивающая функция будет занимать данное положение среди факт политических значений показателей, при котором общее отклонение точек от функции будет наименьшим.
Обоснованную и достоверную оценку имеющимся результатам можно дать, применяя статистические показатели: средний коэффициент увеличения, коэффициент корреляции, остаточная и общая дисперсия, другой индекс корреляции, коэффициент корреляции ряда отклонений и исходного ряда, определенного по разнице выровненных и фактических по любой аналитической функции.
Для того, чтобы проверить гипотезу об отсутствии или наличии автокорреляции применяют таблицы с критическими значениями коэффициента автокорреляции при разных уровнях значимости. Когда табличное значение коефициэнта автокорреляции больше фактического, то возможно утверждать, что автокорреляция устраняется или отсутствует, а означает, возможно применять формулы для возиожностной оценки значений, которые прогнозируются по этому и точками.
Для прогноза были выбраны такие функции, как логарифмическая, линейная, ступенчатая, полиномиальная и экспоненциальная.
Не все выбранные аналитические функции выравнивают хорошо динамический выходной ряд. Об этом говорит значение индекса (коэффициента) корреляции Для того, чтобы прогнозировать, то есть продолжать сформированные тенденции на ближайшую перспективу, можно использовать лишь те функции, для которых индекс (коэффициент) корреляции больше 0,7 К таковым относят линейную, экспоненциальную и полиномиальную функцию. Последняя имеет самый большой коэффициент корреляции, равен 0,847, и самую малую величину остаточной дисперсией.
Порой, само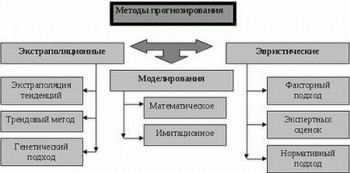
Подставив в полученное уравнение значения периодов предубеждения, определяем прогнозное значение объема товарооборота на такие три месяца: у25 = 654,83; у = 655,93; у \”- 657,07 тыс грн 26 27
Возможность того, что экономический прогнозируемый показатель в заданный момент времени будет равняться значению, которое отвечает точечной прогноза, почти равняться нулю. Потому к точечному прогнозу границы вероятного изменения прогнозируемого значения показателя.
Заметим, что в полученных при прогнозировании оценок доверительных интервалов необходимо отнестись с осторожностью Это связывается со спецификой динамических рядов Их специфичность заключена в том, что увеличение количества наблюдений в статической совокупности дает возможность получить точные характеристики данной совокупности, в то время как аналогичное удлинение ряда динамики приводит не всегда к похожим результатам, особенно в тех ситуациях, когда ряды динамик применяются для прогнозирования. Данное обстоятельство связывается с тем, что информационная ценность уровней потеряется по мере их удаления от периода предубеждение, то есть означает уровни ряда динамики при прогнозировании неравноценно. Потому параметры уравнений аппроксимирующих кривых роста могут обладать погрешности и изменять собственные оценки при исключении части членов ряда или Анне добавил новых членов ряда динамики, что отображается на точности расчетных значений уровней ряда динамики. Помимо этого, параметры моделей тренда, которые получены способом самых малых квадратов, остаются неизменным и в течение рассматриваемого периода. На практике зачастую встречаются случаи, когда параметры моделей изменяются, а процедуры, которые сглаживают при помощи способа самых малых квадратов не могут определить такие изменения.
Поэтому наиболее эффективными являются адаптивные способы, в которых значимость уровней ряда динамики снижается по мере их удаления от прогнозируемого периода. К ним относят: способ текучих средних, способ экспоненциального сглаживания, способ гармонических весов и прочие, включаются в класс адаптивных способов.
Зачастую несколько динамики характеризуются резкими колебаниями показателей по годам. Данные ряды обычно, имеют слабую связь со временем и не проявляют четкой тенденции к изменению. В данной ситуации способы аналитического выравнивания малоэффективен, потому что возможность расчетов резко уменьшается. Доверительные границы прогноза порой оказываются шире, чем колебания показателя в некоторых динамиках.
При прогнозировании на основании временных рядов, которые весьма колеблются, можно применять способ текучих средних, при помощи которого возможно исключить случайные колебания временного ряда.
Интервал, величина которого все еще постоянная, постепенно помещается на одно наблюдение. Когда наблюдается определенная цикличность изменений показателей, интервал текучести равняется длительности циклу. В ситуации отсутствия цикличности в изменении показателей советуется исполнять различный расчет при параметре сглаживания. Лучший вариант определяется на основании дальнейшей оценки и выровненных рядов.
По данным выровненных значений ряда динамики производится подбор формы кривой, которая отражает тенденции развития явления. Полученное уравнение регрессии применяется для определения прогнозного значения исследуемого показатель.
На основании выровненных значений товарных запасов предприятия имеются такие значения коэффициента корреляции. Приведенные данные говорят, что наилучшие итоги должны по данным, которые выровнены на основании уровней исследуемого ряда динамики
Метод экспоненциального сглаживания
Экспоненциальное сглаживание – это выравнивание динамических рядов, весьма колеблются, цели стабильного прогнозирования По данному способу возможно дать обоснованные прогнозы на основе рядов динамики, имеют умеренный связь во времени, и обеспечить больше учета показателей, которые достигнуты за последние годы. Сущность метода оформляется в сглаживании временного ряда при помощи взвешенной текучей средней, в которые и веса подчиняются экспоненциальному закону.
Всякое сглажено значение рассчитано при помощи объединения прошлого текущего значения сглаженного значения и временного ряда. В данной ситуации текущие значения временного ряда разрешаются, учитывая константы, сглаживает.
Мы коротко рассмотрели м етод экстраполяции: методы, применение. Оставляйте свои комментарии или дополнения к материалу.
