На что похожа усеченная пирамида
Что такое усеченная пирамида? Свойства и формулы. Пирамиды индейцев майя
Одним из симметричных полиэдров, свойства которого изучает стереометрия, является пирамида. В данной статье рассмотрим подробнее следующие вопросы: что такое пирамида усеченная, как ее можно получить и какими свойствами она характеризуется.
Полная пирамида
Прежде чем раскрывать вопрос, что такое пирамида усеченная, следует дать определение пирамиды в общем случае.
Под пирамидой в геометрии понимают фигуру в трехмерном пространстве, которая состоит из n треугольных граней и одной n-угольной стороны, которая называется основанием. Представить себе пирамиду достаточно просто: необходимо мысленно соединить все углы n-угольника с некоторой одной точкой в пространстве. Рисунок ниже показывает фигуру, которая при этом получается.
Здесь мы видим, что углы четырехугольного основания соединены отрезками с одной точкой, которая называется вершиной пирамиды. Боковая поверхность фигуры образована четырьмя разными треугольниками.
Если все треугольники боковой поверхности будут одинаковыми и равнобедренными, то такая фигура называется прямой пирамидой. Если к тому же основание будет представлять правильный n-угольник, например, квадрат, то говорят о пирамиде правильной.
Усеченная пирамида
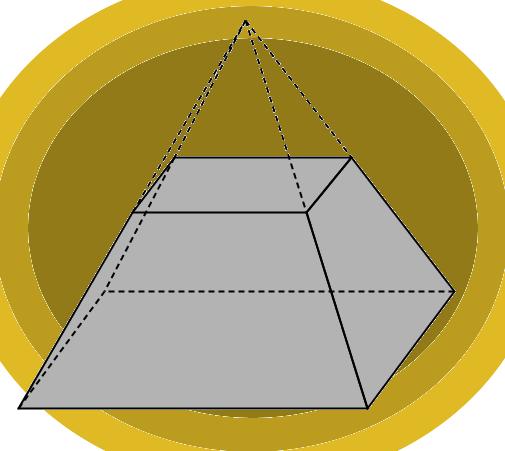
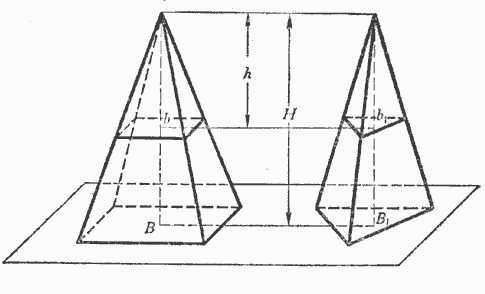
Рассмотренная выше фигура называется полной пирамидой. Теперь покажем, что такое усеченная пирамида и как ее можно получить из полной.
Пусть у нас имеется полная фигура с пятиугольным основанием. Она показана ниже на рисунке слева.
Заметим, что в данном случае мы выбрали секущую плоскость, которая параллельна основанию исходной фигуры. Полученная из правильной фигуры с помощью параллельного сечения усеченная пирамида также будет называться правильной.
Рисунок также показывает, что основания усеченной пирамиды (пятиугольники в примере) образованы подобными правильными многоугольниками, при этом размер верхнего будет всегда меньше, чем нижнего. Боковая поверхность этой фигуры, в отличие от полной пирамиды, образована равнобедренными трапециями.
Если в основании усеченной пирамиды лежит n-угольник, тогда она имеет 2 × n вершин, 3 × n ребер и n + 2 стороны.
Двумя важными геометрическими параметрами рассматриваемой фигуры являются площадь ее поверхности и объем.
Поверхность пирамиды усеченной
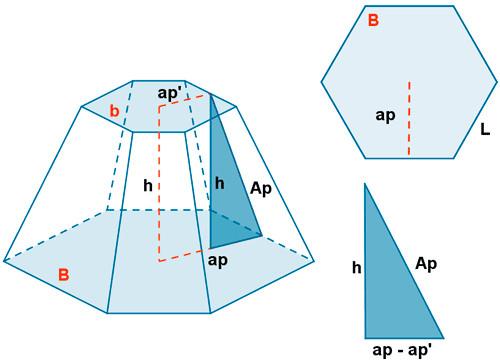
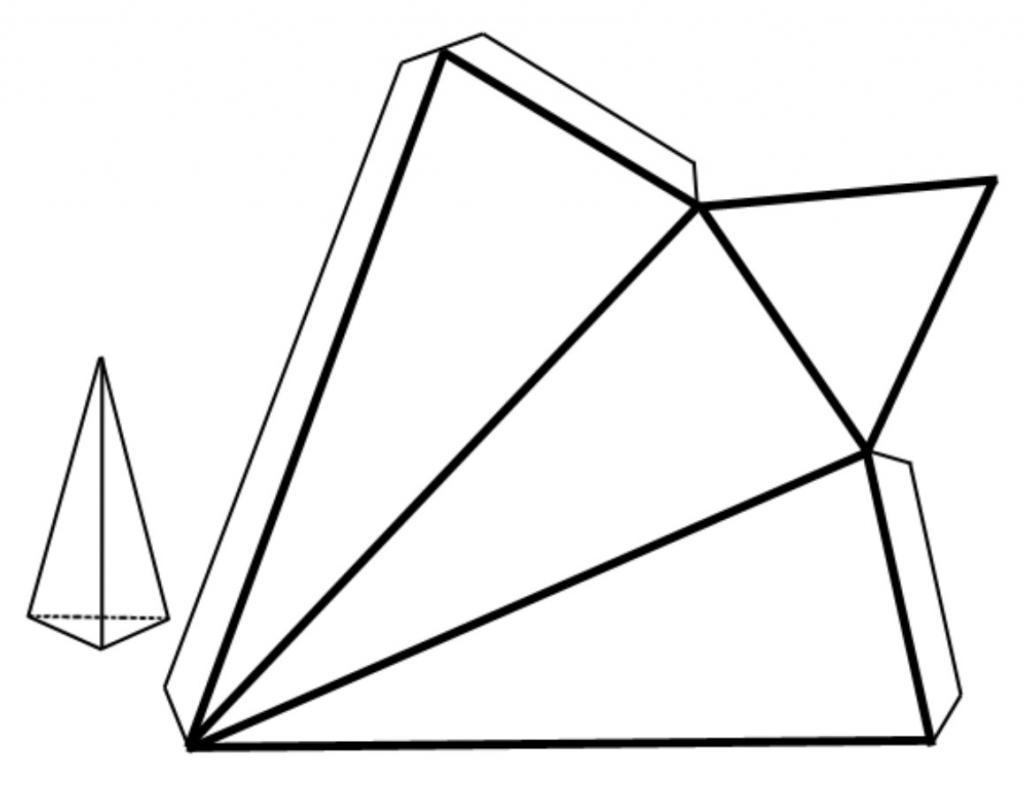
Рассмотрев, что такое усеченная пирамида, перейдем к изучению ее поверхности. Под последней понимают совокупность всех граней, образующих фигуру. Проще всего свойства поверхности изучать на примере развертки. Рисунок ниже показывает развертку для пирамиды с пятиугольными основаниями.
Чтобы вычислить площадь всей ее поверхности, необходимо сложить площадь двух оснований и площадь всех трапеций. Соответствующая формула имеет вид:
S = So1 + So2 + 1/2 × (Po1 + Po2) × Ap.
Например, для случая с четырехугольной правильной усеченной пирамидой эта формула перепишется в виде:
S4 = B2 + b2 + 2 × (B + b ) × Ap.
Объем усеченной пирамиды
Для определения объема рассматриваемой фигуры необходимо знать ее высоту h, а также площади обоих оснований So1 и So2. Если указанные характеристики известны, тогда для определения объема усеченной пирамиды следует воспользоваться формулой:
V = 1/3 × h × (So1 + So2 + √ (So1 × So2)).
Например, для четырехугольной правильной фигуры, длины сторон оснований которой равны B и b, приходим к следующему выражению для объема:
V = 1/3 × h × (B2 + b2 + B × b).
Пример решения задачи
Рассмотрев, что такое усеченная пирамида, а также разобравшись с необходимыми для описания ее характеристик формулами, покажем, как их использовать на практике.
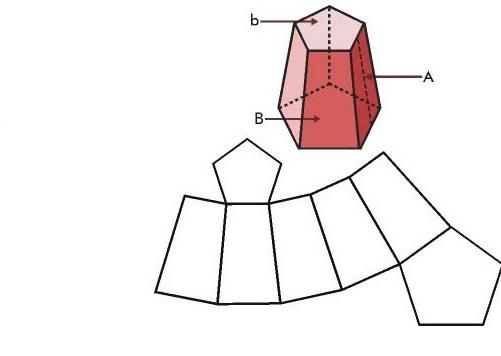
Предположим, что имеется шестиугольная усеченная фигура, которая показана ниже.
Необходимо рассчитать ее объем, если известны стороны оснований B и b и апофема Ap.
Для начала рассчитаем площадь каждого из оснований, которая соответствует площади правильного шестиугольника. Имеем:
Для определения объема необходимо вычислить через Ap высоту h фигуры. Рассматривая изображенный на рисунке прямоугольный треугольник и применяя теорему Пифагора, получаем:
Тогда объем этой шестиугольной усеченной пирамиды будет равен:
Пирамиды индейцев майя
Если египетские пирамиды с точки зрения геометрии представляют собой правильные полные четырехугольные фигуры, то аналогичные сооружения индейцев майя являются четырехугольными усеченными пирамидами.
Эти памятники культуры, сохранившиеся до наших дней, некогда выполняли двойную роль для своих жителей: с одной стороны, они служили гробницей вождям, с другой же стороны, на их верхнем основании располагался храм, где жрецы поклонялись богам.
Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида
Что такое пирамида в общем случае?
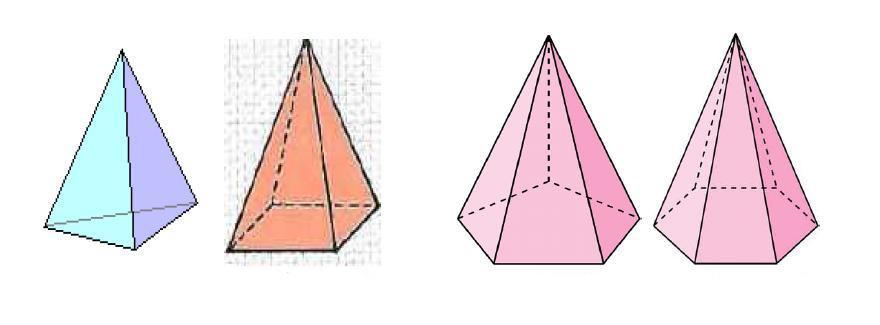
В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.
Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:
Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.
Правильная четырехугольная пирамида
Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.
Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).
Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.
Египетские пирамиды в Гизе являются правильными четырехугольными.
Далее приведем формулы, позволяющие определить все характеристики этой фигуры.
Четыре основных линейных параметра
Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.
Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:
Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):
Очевидно, что боковое ребро b всегда больше апофемы ab.
Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.
Площадь и объем фигуры
Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:
Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.
Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:
S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.
Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:
То есть V равен третьей части произведения высоты фигуры на площадь ее основания.
Свойства правильной усеченной четырехугольной пирамиды
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.
Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.
Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:
V = 1/3 × h × (So1 + So2 + √(So1 × So2))
Пирамида и усеченная пирамида
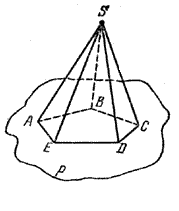
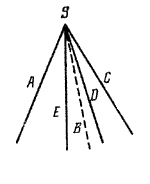
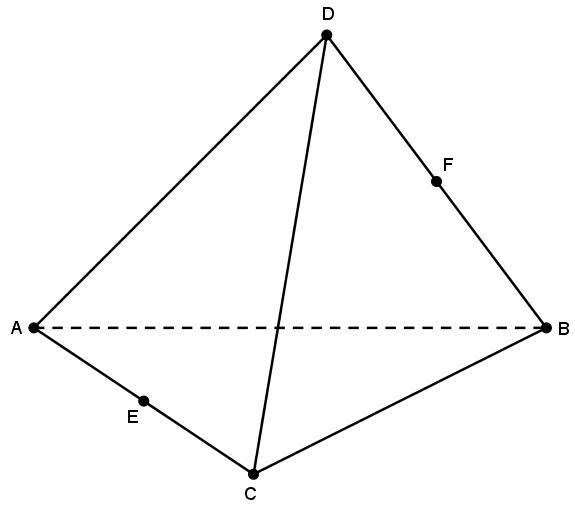
Как можно построить пирамиду? На плоскости р построим какой-либо многоугольник, например пятиугольник ABCDE. Вне плоскости р возьмем точку S. Соединив точку S отрезками со всеми точками многоугольника, получим пирамиду SABCDE (рис.).
Точка S называется вершиной, а многоугольник ABCDE — основанием этой пирамиды. Таким образом, пирамида с вершиной S и основанием ABCDE — это объединение всех отрезков [SM], где М ∈ ABCDE.
Треугольники SAB, SBC, SCD, SDE, SEA называются боковыми гранями пирамиды, общие стороны боковых граней SA, SB, SC, SD, SE — боковыми ребрами.
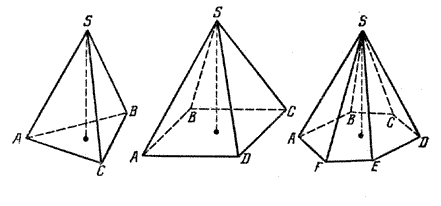
Пирамиды называются треугольными, четырехугольными, п-угольными в зависимости от числа сторон основания. На рис. даны изображения треугольной, четырехугольной и шестиугольной пирамид.
Плоскость, проходящая через вершину пирамиды и диагональ основания, называется диагональной, а полученное сечение — диагональным. На рис. 186 одно из диагональных сечений шестиугольной пирамиды заштриховано.
Отрезок перпендикуляра, проведенного через вершину пирамиды к плоскости ее основания, называется высотой пирамиды (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Пирамида называется правильной, если основание пирамиды—правильный многоугольник и вершина пирамиды проектируется в его центр.
Все боковые грани правильной пирамиды — конгруэнтные равнобедренные треугольники. У правильной пирамиды все боковые ребра конгруэнтны.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды. Все апофемы правильной пирамиды конгруэнтны.
Сумма площадей всех боковых граней пирамиды называется площадью боковой поверхности пирамиды и обозначается через Sбок.
Так как боковая поверхность правильной пирамиды состоит из n конгруэнтных граней, то
где Р — периметр основания пирамиды. Следовательно,
т. е. площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Площадь полной поверхности пирамиды вычисляется по формуле
Объем пирамиды равен одной трети произведения площади ее основания Socн. на высоту Н:
Вывод этой и некоторых других формул будет дан в одной из последующих глав.
Построим теперь пирамиду другим способом. Пусть дан многогранный угол, например, пятигранный, с вершиной S (рис.).
Проведем плоскость р так, чтобы она пересекала все ребра данного многогранного угла в разных точках А, В, С, D, Е (рис.). Тогда пирамиду SABCDE можно рассматривать как пересечение многогранного угла и полупространства с границей р, в котором лежит вершина S.
Очевидно, что число всех граней пирамиды может быть произвольным, но не меньшим четырех. При пересечении трехгранного угла плоскостью получается треугольная пирамида, у которой четыре грани. Любую треугольную пирамиду иногда называют тетраэдром, что означает четырехгранник.
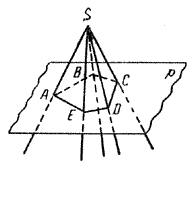
Усеченную пирамиду можно получить, если пирамиду пересечь плоскостью, параллельной плоскости основания.
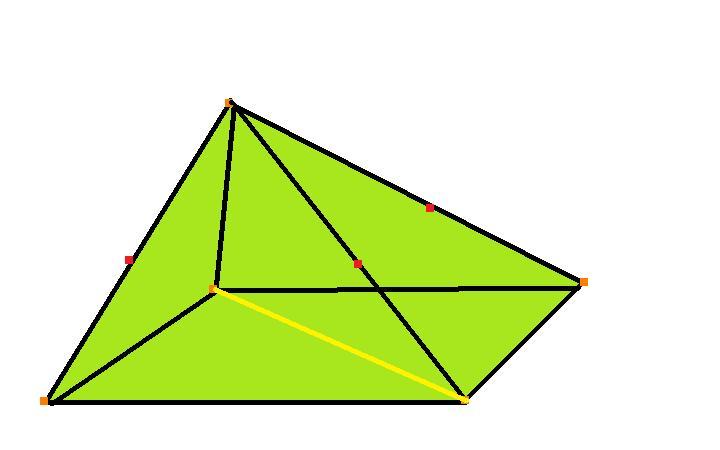
На рис. дано изображение четырехугольной усеченной пирамиды.
Усеченные пирамиды также называются треугольными, четырехугольными, n-угольными в зависимости от числа сторон основания. Из построения усеченной пирамиды следует, что она имеет два основания: верхнее и нижнее. Основания усеченной пирамиды — два многоугольника, стороны которых попарно параллельны. Боковые грани усеченной пирамиды — трапеции.
Высотой усеченной пирамиды называется отрезок перпендикуляра, проведенного из любой точки верхнего основания к плоскости нижнего.
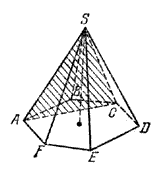
Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и плоскостью сечения, параллельной основанию. Высота боковой грани правильной усеченной пирамиды (трапеции) называется апофемой.
Можно доказать, что у правильной усеченной пирамиды боковые ребра конгруэнтны, все боковые грани конгруэнтны, все апофемы конгруэнтны.
Если в правильной усеченной n-угольной пирамиде через а и bn обозначить длины сторон верхнего и нижнего оснований, а через h — длину апофемы, то площадь каждой боковой грани пирамиды равна
Так как па = Р и nbn = Р1 — периметры оснований усеченной пирамиды, то
т. е. площадь боковой поверхности правильной усеченной пирамиды равна половине произведения суммы периметров ее оснований на апофему.
Сечение, параллельное основанию пирамиды
1) боковые ребра и высота разделятся на пропорциональные части;
2) в сечении получится многоугольник, подобный основанию;
3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
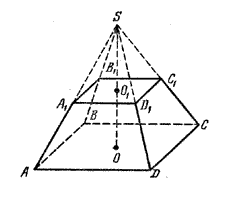
Теорему достаточно доказать для треугольной пирамиды.
Так как параллельные плоскости пересекаются третьей плоскостью по параллельным прямым, то (АВ) || (А1В1), (BС) ||( В1C1), (AС) || (A1С1) (рис.).
Параллельные прямые рассекают стороны угла на пропорциональные части, и поэтому
Соответственные углы треугольников ABC и A1B1C1 конгруэнтны, как углы с параллельными и одинаково направленными сторонами. Поэтому
Площади подобных треугольников относятся, как квадраты соответствующих сторон:
Теорема. Если две пирамиды с равными высотами рассечены на одинаковом расстоянии от вершины плоскостями, параллельными основаниям, то площади сечений пропорциональны площадям оснований.
Пусть (черт. 84) В и В1— площади оснований двух пирамид, H — высота каждой из них, b и b1 — площади сечений плоскостями, параллельными основаниям и удалёнными от вершин на одно и то же расстояние h.
Согласно предыдущей теореме мы будем иметь:
Формулы и свойства правильной треугольной пирамиды. Усеченная треугольная пирамида
Геометрические представления о фигуре
Прежде чем переходить к рассмотрению свойств правильной пирамиды треугольной, разберемся подробнее, о какой фигуре идет речь.
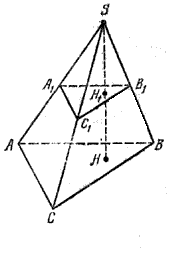
Предположим, что имеется произвольный треугольник в трехмерном пространстве. Выберем в этом пространстве любую точку, которая в плоскости треугольника не лежит, и соединим ее с тремя вершинами треугольника. Мы получили треугольную пирамиду.
Поскольку фигура образована четырьмя сторонами, ее также называют тетраэдром.
Правильная пирамида
Выше была рассмотрена произвольная фигура с треугольным основанием. Теперь предположим, что мы провели перпендикулярный отрезок из вершины пирамиды к ее основанию. Этот отрезок называется высотой. Очевидно, что можно провести 4 разные высоты для фигуры. Если высота пересекает в геометрическом центре треугольное основание, то такая пирамида называется прямой.
Прямая пирамида, основанием которой будет треугольник равносторонний, называется правильной. Для нее все три треугольника, образующих боковую поверхность фигуры, являются равнобедренными и равны друг другу. Частным случаем правильной пирамиды является ситуация, когда все четыре стороны являются равносторонними одинаковыми треугольниками.
Рассмотрим свойства правильной пирамиды треугольной и приведем соответствующие формулы для вычисления ее параметров.
Сторона основания, высота, боковое ребро и апотема
Любые два из перечисленных параметров однозначно определяют остальные две характеристики. Приведем формулы, которые связывают названные величины.
Предположим, что сторона основания треугольной пирамиды правильной равна a. Длина ее бокового ребра равна b. Чему будут равны высота правильной пирамиды треугольной и ее апотема.
Для высоты h получаем выражение:
Эта формула следует из теоремы Пифагора для прямоугольного треугольника, сторонами которого являются боковое ребро, высота и 2/3 высоты основания.
Апотемой пирамиды называется высота для любого бокового треугольника. Длина апотемы ab равна:
Из этих формул видно, что какими бы ни были сторона основания пирамиды треугольной правильной и длина ее бокового ребра, апотема всегда будет больше высоты пирамиды.
Представленные две формулы содержат все четыре линейные характеристики рассматриваемой фигуры. Поэтому по известным двум из них можно найти остальные, решая систему из записанных равенств.
Объем фигуры
Для абсолютно любой пирамиды (в том числе наклонной) значение объема пространства, ограниченного ею, можно определить, зная высоту фигуры и площадь ее основания. Соответствующая формула имеет вид:
Применяя это выражение для рассматриваемой фигуры, получим следующую формулу:
Не сложно получить формулу для объема тетраэдра, у которого все стороны равны между собой и представляют равносторонние треугольники. В таком случае объем фигуры определится по формуле:
То есть он определяется длиной стороны a однозначно.
Площадь поверхности
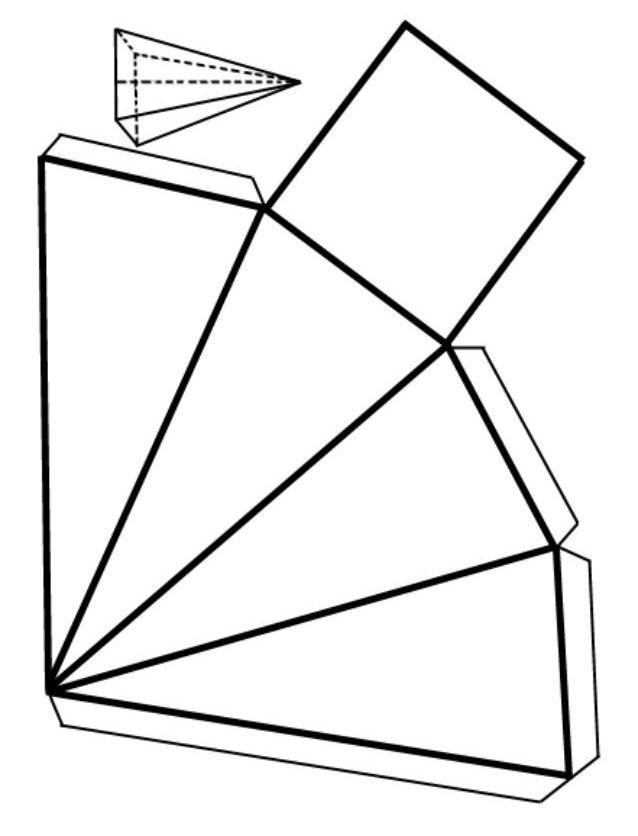
Продолжим рассматривать свойства пирамиды треугольной правильной. Общая площадь всех граней фигуры называется площадью ее поверхности. Последнюю удобно изучать, рассматривая соответствующую развертку. На рисунке ниже показано, как выглядит развертка правильной пирамиды треугольной.
Предположим, что нам известны высота h и сторона основания a фигуры. Тогда площадь ее основания будет равна:
Получить это выражение может каждый школьник, если вспомнит, как находить площадь треугольника, а также учтет, что высота равностороннего треугольника также является биссектрисой и медианой.
Площадь боковой поверхности, образованной тремя одинаковыми равнобедренными треугольниками, составляет:
Данное равенство следует из выражения апотемы пирамиды через высоту и длину основания.
Полная площадь поверхности фигуры равна:
S = So + Sb = √3/4*a2 + 3/2*√(a2/12+h2)*a
Заметим, что для тетраэдра, у которого все четыре стороны являются одинаковыми равносторонними треугольниками, площадь S будет равна:
Свойства правильной усеченной пирамиды треугольной
Если у рассмотренной треугольной пирамиды плоскостью, параллельной основанию, срезать верх, то оставшаяся нижняя часть будет называться усеченной пирамидой.
В случае правильной пирамиды с треугольным основанием в результате описанного метода сечения получается новый треугольник, который также является равносторонним, но имеет меньшую длину стороны, чем сторона основания. Усеченная треугольная пирамида показана ниже.
Мы видим, что эта фигура уже ограничена двумя треугольными основаниями и тремя равнобедренными трапециями.
Предположим, что высота полученной фигуры равна h, длины сторон нижнего и верхнего оснований составляют a1 и a2 соответственно, а апотема (высота трапеции) равна ab. Тогда площадь поверхности усеченной пирамиды можно вычислить по формуле:
S = 3/2*(a1+a2)*ab + √3/4*(a12 + a22)
Объем фигуры рассчитывается следующим образом:
V = √3/12*h*(a12 + a22 + a1*a2)
Для однозначного определения характеристик усеченной пирамиды необходимо знать три ее параметра, что демонстрируют приведенные формулы.
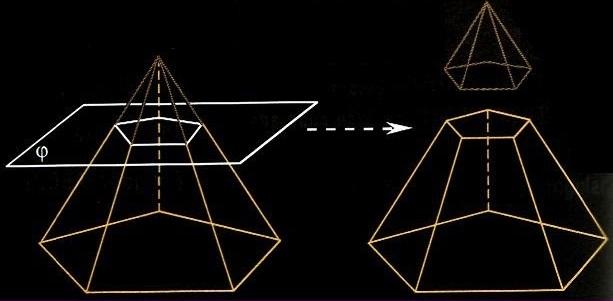
Усечённая пирамида
Усечё́нная пирами́да — многогранник, образованный пирамидой и её сечением, параллельным основанию.
Содержание
Произвольная усечённая пирамида
Формулы для усечённой пирамиды
Объём пирамиды 


Площадь боковой поверхности 
Правильная усечённая пирамида
Определение
Правильная усечённая пирамида — многогранник, образованный правильной пирамидой и её сечением, параллельным основанию.







 Многогранники
Многогранники