На что указывает основание системы счисления
Системы счисления. Основные понятия.
Запись числа в некоторой системе счисления называется кодом числа.
Количество разрядов в записи числа называют разрядностью и совпадает с его длиной.
Системы счисления делятся на позиционные и непозиционные. Позиционные системы счисления делятся
на однородные и смешанные.
Непозиционная система счисления — древнейшая, здесь все цифры числа имеют величину, которая не
зависит от позиции (разряда).
Т.е., если есть 5 палочек, значит число соответственно равно 5, так как каждой палочке, вне зависимости
от её места в строке, соответствует только 1 предмет.
Позиционная система счисления — значение каждой цифры зависит от позиции (разряда) этой цифры в числе.
Например, стандартная 10-я система счисления является позиционной. Допустим дано число 453.
Цифра 4 означает число сотен и соответствует числу 400, 5 — кол-во десятков и соответствует значению
50, а 3 — единицы и значению 3. Легко заметить, что с увеличением разряда увеличивается значение.
Таким образом, заданное число запишем в виде суммы 400+50+3=453.
Однородная система — для каждого разряда (позиции) числа набор допустимых символов (цифр)
одинаковый. Как пример снова используем 10-ю систему. Если записывать число в однородной 10-й системе,
(1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, так как символ F не входит в набор цифр от 0 до 9.
Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может
отличаться от наборов в других разрядах. Хороший пример — система измерения времени. В разряде
В непозиционных системах счисления вес цифры не зависим от позиции, которую она занимает в
числе. К примеру, в римской системе счисления в числе XXXII (32) вес цифры X в каждой позиции
Цифрами в римской системе служат: I(1), V(5), X(10), L(50), C(100), D(500), M(1000).
Размер числа в римской системе счисления определяют как сумму либо разность цифр в числе. Когда
меньшая цифра стоит слева от большей – она вычитается, когда справа – прибавляется.
Самая первая система счисления — единичная (непозиционная).
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в
последовательности цифр, которые изображают число.
Каждая позиционная система характеризуется своим основанием.
Основание позиционной системы счисления – это количество разных знаков либо символов, которые
используются для изображения цифр в этой системе.
множество позиционных систем.
Перевод систем счисления. Числа можно перевести из одной системы счисления в другую.
Таблица соответствия цифр в различных системах счисления.
Системы счисления
Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков.
Цифры бывают разные: самыми распространёнными являются арабские цифры, представляемые знаками от нуля (0) до девяти (9); менее распространены римские цифры, их можно встретить на циферблате часов или в обозначении века (XIX век).
Поскольку чисел гораздо больше чем цифр, то для записи числа обычно используется набор (комбинация) цифр. Только для небольшого количества чисел — для самых малых по величине целых чисел — бывает достаточно одной цифры. Существует много способов записи чисел с помощью цифр, называемых системой счисления. Величина числа может зависеть от порядка цифр в записи, а может и не зависеть. Это свойство определяется системой счисления и служит основанием для простейшей классификации таких систем, что позволяет все системы счисления разделить на четыре класса (группы):
Позиционные системы счисления подробно рассмотрены ниже, после краткого обзора смешанных и непозиционных систем.
Денежные знаки — это пример смешанной системы счисления.
Сейчас в России используются монеты и купюры следующих номиналов: по 5, 10, 50 копеек и по 1, 2, 5, 10, 50, 100, 200, 500, 1000, 2000, 5000 рублей. Чтобы получить некоторую сумму в рублях, нужно использовать некоторое количество денежных знаков различного достоинства.
Предположим, что пылесос стоит 6379 рублей. Для покупки можно использовать шесть купюр по тысяче рублей, три купюры по сто рублей, одну пятидесятирублёвую купюру, две десятки, одну пятирублёвую монету и две монеты по два рубля. Если записать количество купюр или монет начиная с 1000 руб. и заканчивая пятью копейками, заменяя нулями неиспользуемые номиналы, то получится число 600312120000.
Если перемешать цифры в числе 600312120000, оно представит ложную цену пылесоса. Следовательно, такая запись относится к позиционным системам.
В непозиционных системах счисления величина числа не зависит от положения цифр в записи. Если к каждой цифре приписать знак номинала, то такие составные знаки (цифра + номинал) уже можно перемешивать, то есть такая запись является непозиционной.
Примером «рафинированной» непозиционной системы счисления является римская система.
Содержание
Позиционные системы счисления
Введение
Позиционные системы счисления — это системы счисления, в которых значение цифры напрямую зависит от её положения в числе.
Например, число 01 обозначает единицу, 10 — десять.
Позиционные системы счисления позволяют легко производить арифметические расчёты.
Представление чисел с помощью арабских цифр — самая распространённая позиционная система счисления, она называется «десятичной системой счисления». Десятичной системой она называется потому, что использует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Заметьте: максимальная цифра (9) на единицу меньше количества цифр (10).
Для составления машинных кодов удобно использовать не десятичную, а двоичную систему счисления, содержащую только две цифры, 0 и 1. Обратите внимание, что в двоичной системе максимальная цифра 1.
Программисты для вычислений также пользуются ещё восьмеричной и шестнадцатеричной системами счисления.
Количество цифр, используемых в системе счисления, называется её «основанием». В десятичной системе основание равно десяти, в двоичной системе — двум, ну а в восьмеричной и шестнадцатеричной — соответственно, восьми и шестнадцати. То есть в ручной системе счисления количество цифр равно р и используются цифры от 0 до р-1.
Зависимость плотности записи информации от основания системы счисления
Удельная натурально логарифмическая плотность записи числа зависит от основания системы счисления х и выражается функцией y=ln(x)/x. Эта функция имеет максимум при x=e=2,718281828….
То есть система счисления с наибольшей плотностью записи имеет не целочисленное основание.
Из целочисленных систем счисления наибольшей плотностью записи информации обладает троичная система счисления, то есть система с основанием равным трём.
Преобразование чисел
Посмотрим чему равны числа из примеров. Используем только что приведённую формулу:
Что и следовало ожидать, получили: 11001 2 <\displaystyle 11001_<2>> 
Представим число 25 в троичной системе счисления:
Получили число: 221 3 <\displaystyle 221_<3>> 
Для закрепления наших знаний проделаем вычисления для восьмеричной и десятичной систем счисления.
Восьмеричная система счисления:
Десятичная система счисления:
Чтобы ещё лучше понять перевод в различные системы счислений, посмотрим, какие трансформации происходят внутри числа 4567 10 <\displaystyle 4567_<10>> 
Представим это число в виде
4 ⋅ 10 3 + 5 ⋅ 10 2 + 6 ⋅ 10 1 + 7 ⋅ 10 0 = 4 ⋅ 1000 + 5 ⋅ 100 + 6 ⋅ 10 + 7 <\displaystyle 4\cdot 10^<3>+5\cdot 10^<2>+6\cdot 10^<1>+7\cdot 10^<0>=4\cdot 1000+5\cdot 100+6\cdot 10+7> 
Шестидесятеричная система счисления
То, как мы представляем время на часах, это пример шестидесятеричной позиционной системы счисления. В представлении времени используется три позиции: для часов, минут и секунд; так как для каждой позиции приходится использовать 60 цифр, а у нас только десять цифр, то для каждой шестидесятиричной позиции используется две десятичные цифры (00, 01, 02, …, 59), а позиции разделяются двоеточием.
Чтобы получить время в секундах мы должны посчитать вот по такой формуле:
h 60 2 + m 60 1 + s 60 0 = h 3600 + m 60 + s <\displaystyle h60^<2>+m60^<1>+s60^<0>=h3600+m60+s>
Рассмотрим действия с шестидесятеричной системой на двух небольших задачках:
Чтобы производить вычисления в шестидесятеричной системе счисления нужно знать таблицу сложений и умножений шестидесятеричных чисел. Каждая таблица очень большая, она размером 60х60 ячеек, мы то обычную таблицу умножения еле запомнили, а уж выучить шестидесятиричную таблицу умножения нам врядли окажется по силам.
Чтобы решить эти задачи можно посчитать всё в десятичной системе, а потом результат перевести назад в шестидесятиричную систему.
Приступим. Чтобы перевести 45 минут в количество секунд, нужно просто, подставить числа в верхнюю формулу: h равняется нулю, m равняется 45 и s — нулю, получаем
Ответ на первый вопрос: пирог нужно печь в духовке 2700 секунд.
Ответ на второй вопрос: чтобы испечь десять пирогов потребуется 7 часов 30 минут и 0 секунд.
Двоичная система счисления
В компьютерной технике очень часто используется двоичная система счисления. Такую систему очень легко реализовать в электронике (полупроводниковые транзисторы и микросхемы), так как для неё требуется всего два устойчивых состояния (0 и 1).
Двоичная система счисления может быть непозиционной и позиционной системой. В ней используется две цифры: 0 и 1. В реальном устройстве это может быть реализовано присутствием какого-либо физического явления или его отсутствием. Например: есть электрический заряд или его нет, есть напряжение или нет, есть ток или нет, есть сопротивление или нет, отражает свет или нет, намагничено или не намагничено, есть отверстие или нет и т.п.
Мы уже знаем, как переводить числа в различные системы счисления. Посмотрим, как это происходит с двоичной системой счисления. Переведём число из двоичной системы счисления в десятичную.
10101010 2 = 1 ⋅ 2 7 + 0 ⋅ 2 6 + 1 ⋅ 2 5 + 0 ⋅ 2 4 + 1 ⋅ 2 3 + 0 ⋅ 2 2 + 1 ⋅ 2 1 + 0 ⋅ 2 0 = 128 + 32 + 8 + 2 = 170 <\displaystyle 10101010_<2>=1\cdot 2^<7>+0\cdot 2^<6>+1\cdot 2^<5>+0\cdot 2^<4>+1\cdot 2^<3>+0\cdot 2^<2>+1\cdot 2^<1>+0\cdot 2^<0>=128+32+8+2=170> 
Вы это можете проверить на программе-калькуляторе (gcalctool в gnome, Kcalc в KDE, или калькулятор в Windows). Он умеет производить расчёты в двоичной, восьмеричной и шестнадцатиричной системах счисления. Теперь вы знаете, как он это проделывает. Если вы захотите посвятить свою жизнь программированию, то вам часто придётся работать со степенями двойки. Ниже представлена таблица:
| Степень | Значение |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| 9 | 512 |
| 10 | 1024 |
| 11 | 2048 |
| 12 | 4096 |
| 13 | 8192 |
| 14 | 16384 |
| 15 | 32768 |
| 16 | 65536 |
Произведём обратное преобразование. Чтобы преобразовать число в десятичном виде к двоичному, нам нужно будет делить всё время на два и смотреть на остаток от деления. Возьмём число 33.
Возьмём число 55. Посмотрим, что получится.
Ниже приведены ещё примеры со сложением, вычитанием, умножением и делением.
Программа двоичного представления десятичного числа (Написана на Си)
Троичная система счисления
Из целочисленных систем счисления обладает наибольшей плотностью записи информации. Первая троичная ЭВМ «Сетунь» была построена в 1958 году Н. П. Брусенцовым в МГУ.
Четверичная система счисления
Обладает такой же плотностью записи, как и двоичная система счисления. Таблица такая же, как и для двоичной системы счисления.
Восьмеричная и шестнадцатеричная системы счислений
Компьютерам очень удобно оперировать двоичными числами, но люди не привыкли работать с большим количеством цифр. Например, чтобы представить в двоичном виде число 1234 потребуется больше 10 двоичных цифр (10011010010). Поэтому были придуманы восьмеричная и шестнадцатеричная системы счислений. Они удобны как и десятичные числа тем, что для представления числа требуется меньшее количество разрядов. А по сравнению с десятичными числами, перевод в двоичное представление очень простой. Это как будто мы двоичное число разбили на группы по три или четыре разряда и каждой двоичной комбинации придумали значок. Вот таблица для восьмеричных цифр:
| Двоичная комбинация | Значок |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
А вот таблица для шестнадцатеричных цифр:
| Двоичная комбинация | Значок |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Перевод произвести очень просто, посмотрим на примере числа 010011010010.
Разбиваем его на группы по три цифры: 010 011 010 010. И по таблице переводим: 2322 8 <\displaystyle 2322_<8>> 
Чтобы перевести число в шестнадцатеричное представление разбиваем двоичное число на группы по четыре цифры: 0100 1101 0010. И по таблице переводим: 4 D 2 16 <\displaystyle 4D2_<16>> 
Системы счисления
Система счисления — это совокупность правил записи чисел посредством конечного набора символов (цифр).
Системы счисления бывают:
Непозиционные системы счисления
Примеры: унарная, римская, древнерусская и др.
Позиционные системы счисления
Основание системы счисления —
количество различных цифр, используемых в этой системе.
отношение количественного эквивалента цифры в этом разряде к количественному эквиваленту той же цифры в нулевом разряде
где i — номер разряда, а s — основание системы счисления.
Разряды числа нумеруются справа налево, причем младший разряд целой части (стоящий перед разделителем — запятой или точкой) имеет номер ноль. Разряды дробной части имеют отрицательные номера:
По определению веса разряда
где i — номер разряда, а s — основание системы счисления.
Тогда, обозначив цифры числа как ai, любое число, записанное в позиционной системе счисления, можем представить в виде:
Например, для системы счисления с основанием 4:
Выполнив вычисления, мы получим значение исходного числа, записанное в десятичной системе счисления (точнее, в той, в которой производим вычисления). В данном случае:
= 1⋅64 + 3⋅16 + 0⋅4 + 2⋅1 + 2⋅0,25 =
= 64 + 48 + 2 + 0,5 = 114,5
Таким образом, для перевода числа из любой системы счисления в десятичную следует:
Вспомним пример перевода из системы счисления с основанием 4 в десятичную:
13024 = 1⋅4 3 + 3⋅4 2 + 0⋅4 1 + 2⋅4 0 = 114
Иначе это можно записать так:
114 = ((1 ⋅ 4 + 3) ⋅ 4 + 0) ⋅ 4 + 2 = 13024
Отсюда видно, что при делении 114 на 4 нацело в остатке должно остаться 2 — это младшая цифра при записи в четверичной системе. Частное же будет равно
Деление его на 4 даст остаток — следующую цифру (0) и частное 1 ⋅ 4 + 3. Продолжая действия, получим аналогичным образом и оставшиеся цифры.
В общем случае для перевода целой части числа из десятичной системы счисления в систему с каким-либо другим основанием необходимо:
Что такое основание и база системы счисления?
Определение: Основанием системы счисления называется количество разных знаков либо символов, которые
используются для изображения цифр в этой системе.
Основанием принимают всякое натуральное число — 2, 3, 4, 16 и т.д. То есть, существует безграничное
множество позиционных систем. Например для десятичной системы основание равно 10.
Определить основание очень легко, нужно только пересчитать количество значащих цифр в системе. Если проще, то это число, с которого начинается второй разряд у числа. Мы, например, используем цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Их ровно 10, поэтому основание нашей системы счисления тоже 10, и система счисления называется “десятичная”. В вышеприведенном примере используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (вспомогательные 10, 100, 1000, 10000 и т. д. не в счет). Основных цифр здесь тоже 10, и система счисления – десятичная.
База системы — это последовательность цифр, используемых для записи числа. Ни в одной системе нет цифры, равной основанию системы.
Как можно догадаться, сколько есть чисел, столько же может быть и оснований систем счисления. Но используются только самые удобные основания систем счисления. Как вы думаете, почему основание самой употребительной человеческой системы счисления 10? Да, именно потому, что на руках у нас 10 пальцев. “Но на одной то руке всего пять пальцев” – скажут некоторые и будут правы. История человечества знает примеры пятеричных систем счисления. “А с ногами – двадцать пальцев” – скажут другие, и будут тоже абсолютно правы. Именно так считали индейцы Майя. Это даже видно по их цифрам.
Десятичная система счисления
Мы все привыкли при счете использовать цифры и числа, знакомые нам с детства. Один, два, три, четыре и т.д. В нашей повседневной системе счисления всего десять цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), из которых мы составляем любые числа. Дойдя до десятка, мы добавляем единицу к разряду левее и снова начинаем в самом правом разряде отсчитывать с нуля. Такая система счисления называется десятичной.
Не трудно догадаться, что выбрали её наши предки потому что количество палецев на обеих руках равно десяти. Но какие еще бывают системы счисления? Всегда ли использовали десятичную систему счисления или были и другие?
История возникновения систем счисления
До изобретения нуля для записи чисел применялись специальные знаки. У каждого народа они были своими. В Древнем Риме, например, господствовала непозиционная система счисления.
Систему счисления называют непозиционной, если значение цифры не зависит от занимаемого ею места. Наиболее совершенными системами счисления считались системы счисления, которые использовались на Руси и в Древней Греции.
В них большие числа обозначали буквами, но с добавлением дополнительных значков (1 – a, 100 –i и т.д.). Другой непозиционной системой счисления являлась система, которая использовалась в Древнем Вавилоне. В своей системе жители Вавилона использовали запись в «два этажа» и всего три знака: Единица в вавилонской системе счисления — для единицы, Десяток в вавилонской системе счисления — для десятка и Нуль в вавилонской системе счисления — для нуля.
Позиционные системы счисления
Шагом вперед стали позиционные системы. Сейчас повсеместно победила десятичная, но есть и другие системы, часто используемые в прикладных науках. Примером такой системы счисления может служить двоичная система счисления.
Двоичная система счисления
Именно на ней общаются компьютеры и вся электроника у вас дома. В этой системе счисления используются всего две цифры: 0 и 1. Вы спросите, почему было не научить компьютер считать до десяти, как человека? Ответ кроется на поверхности.
Научить машину различать два символа легко: включено – значит, 1, выключено – значит 0; есть ток – 1, нет тока – 0. Были попытки сделать машины, которые могли бы различать большее количество цифр. Но все они оказались ненадежными, компьютеры все время путали: то ли 1 к ним пришло, то ли 2.
Нас окружает множество различных систем счисления. Каждая из них полезна в своей области. И ответ на вопрос, какую и когда использовать, остается за нами.
Основы систем счисления
Изучая кодировки, я понял, что недостаточно хорошо понимаю системы счислений. Тем не менее, часто использовал 2-, 8-, 10-, 16-ю системы, переводил одну в другую, но делалось все на “автомате”. Прочитав множество публикаций, я был удивлен отсутствием единой, написанной простым языком, статьи по столь базовому материалу. Именно поэтому решил написать свою, в которой постарался доступно и по порядку изложить основы систем счисления.
Введение
Система счисления — это способ записи (представления) чисел.
Что под этим подразумевается? Например, вы видите перед собой несколько деревьев. Ваша задача — их посчитать. Для этого можно — загибать пальцы, делать зарубки на камне (одно дерево — один палец\зарубка) или сопоставить 10 деревьям какой-нибудь предмет, например, камень, а единичному экземпляру — палочку и выкладывать их на землю по мере подсчета. В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором — композиция камней и палочек, где слева — камни, а справа — палочки
Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные.
Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.
Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.
Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9.
Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.
Непозиционные системы
Как только люди научились считать — возникла потребность записи чисел. В начале все было просто — зарубка или черточка на какой-нибудь поверхности соответствовала одному предмету, например, одному фрукту. Так появилась первая система счисления — единичная.
Единичная система счисления
Число в этой системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.
Но эта система обладает явными неудобствами — чем больше число — тем длиннее строка из палочек. Помимо этого, можно легко ошибиться при записи числа, добавив случайно лишнюю палочку или, наоборот, не дописав.
Для удобства, люди стали группировать палочки по 3, 5, 10 штук. При этом, каждой группе соответствовал определенный знак или предмет. Изначально для подсчета использовались пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.
Древнеегипетская десятичная система
Почему она называется десятичной? Как писалось выше — люди стали группировать символы. В Египте — выбрали группировку по 10, оставив без изменений цифру “1”. В данном случае, число 10 называется основанием десятичной системы счисления, а каждый символ — представление числа 10 в какой-то степени.
Числа в древнеегипетской системе счисления записывались, как комбинация этих
символов, каждый из которых повторялся не более девяти раз. Итоговое значение равнялось сумме элементов числа. Стоит отметить, что такой способ получения значения свойственен каждой непозиционной системе счисления. Примером может служить число 345:
Вавилонская шестидесятеричная система
В отличии от египетской, в вавилонской системе использовалось всего 2 символа: “прямой” клин — для обозначения единиц и “лежачий” — для десятков. Чтобы определить значение числа необходимо изображение числа разбить на разряды справа налево. Новый разряд начинается с появления прямого клина после лежачего. В качестве примера возьмем число 32: 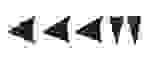
Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной.
Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а большие значения — в позиционной с основанием 60. Число 92: 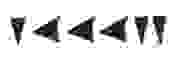
Запись числа была неоднозначной, поскольку не существовало цифры обозначающей ноль. Представление числа 92 могло обозначать не только 92=60+32, но и, например, 3632=3600+32. Для определения абсолютного значения числа был введен специальный символ для обозначения пропущенного шестидесятеричного разряда, что соответствует появлению цифры 0 в записи десятичного числа: 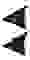
Теперь число 3632 следует записывать, как:
Шестидесятеричная вавилонская система — первая система счисления, частично основанная на позиционном принципе. Данная система счисления используется и сегодня, например, при определении времени — час состоит из 60 минут, а минута из 60 секунд.
Римская система
Римская система не сильно отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C, D и M соответственно. Число в римской системе счисления — это набор стоящих подряд цифр.
Позиционные системы счисления
Как упоминалось выше — первые предпосылки к появлению позиционной системы возникли в древнем Вавилоне. В Индии система приняла форму позиционной десятичной нумерации с применением нуля, а у индусов эту систему чисел заимствовали арабы, от которых её переняли европейцы. По каким-то причинам, в Европе за этой системой закрепилось название “арабская”.
Десятичная система счисления
Это одна из самых распространенных систем счисления. Именно её мы используем, когда называем цену товара и произносим номер автобуса. В каждом разряде (позиции) может использоваться только одна цифра из диапазона от 0 до 9. Основанием системы является число 10.
Для примера возьмем число 503. Если бы это число было записано в непозиционной системе, то его значение равнялось 5+0+3 = 8. Но у нас — позиционная система и значит каждую цифру числа необходимо умножить на основание системы, в данном случае число “10”, возведенное в степень, равную номеру разряда. Получается, значение равно 5*10 2 + 0*10 1 + 3*10 0 = 500+0+3 = 503. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса. Таким образом, 503 = 50310.
Помимо десятичной системы, отдельного внимания заслуживают 2-, 8-, 16-ая системы.
Двоичная система счисления
Эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную нам 10-ю? Первую вычислительную машину создал Блез Паскаль, использовавший в ней десятичную систему, которая оказалась неудобной в современных электронных машинах, поскольку требовалось производство устройств, способных работать в 10 состояниях, что увеличивало их цену и итоговые размеры машины. Этих недостатков лишены элементы, работающие в 2-ой системе. Тем не менее, рассматриваемая система была создана за долго до изобретения вычислительных машин и уходит “корнями” в цивилизацию Инков, где использовались кипу — сложные верёвочные сплетения и узелки.
Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1.
Примером может служить число 101. Оно аналогично числу 5 в десятичной системе счисления. Для того, чтобы перевести из 2-й в 10-ю необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду. Таким образом, число 1012 = 1*2 2 + 0*2 1 + 1*2 0 = 4+0+1 = 510.
Хорошо, для машин 2-я система счисления удобнее, но мы ведь часто видим, используем на компьютере числа в 10-й системе. Как же тогда машина определяет какую цифру вводит пользователь? Как переводит число из одной системы в другую, ведь в её распоряжении всего 2 символа — 0 и 1?
Чтобы компьютер мог работать с двоичными числами (кодами), необходимо чтобы они где-то хранились. Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он может находится в 2-х состояниях, одно из которых соответствует нулю, другое — единице. Для запоминания отдельного числа используется регистр — группа триггеров, число которых соответствует количеству разрядов в двоичном числе. А совокупность регистров — это оперативная память. Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со словами осуществляет арифметико-логическое устройство (АЛУ). Для упрощения доступа к регистрам их нумеруют. Номер называется адресом регистра. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся, а не сами числа. Адреса записываются в 8- и 16-ричной системах (о них будет рассказано ниже), поскольку переход от них к двоичной системе и обратно осуществляется достаточно просто. Для перевода из 2-й в 8-ю число необходимо разбить на группы по 3 разряда справа налево, а для перехода к 16-ой — по 4. Если в крайней левой группе цифр не достает разрядов, то они заполняются слева нулями, которые называются ведущими. В качестве примера возьмем число 1011002. В восьмеричной — это 101 100 = 548, а в шестнадцатеричной — 0010 1100 = 2С16. Отлично, но почему на экране мы видим десятичные числа и буквы? При нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц). Программа драйвер клавиатуры и экрана обращается к кодовой таблице символов (например, Unicode, позволяющая закодировать 65536 символов), определяет какому символу соответствует полученный код и отображает его на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде, а программным способом преобразуются в изображения на экране.
Восьмеричная система счисления
8-я система счисления, как и двоичная, часто применяется в цифровой технике. Имеет основание 8 и использует для записи числа цифры от 0 до 7.
Шестнадцатеричная система счисления
Шестнадцатеричная система широко используется в современных компьютерах, например при помощи неё указывается цвет: #FFFFFF — белый цвет. Рассматриваемая система имеет основание 16 и использует для записи числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, где буквы равны 10, 11, 12, 13, 14, 15 соответственно.
Помимо рассмотренных позиционных систем счисления, существуют и другие, например:
1) Троичная
2) Четверичная
3) Двенадцатеричная
Позиционные системы подразделяются на однородные и смешанные.
Однородные позиционные системы счисления
Определение, данное в начале статьи, достаточно полно описывает однородные системы, поэтому уточнение — излишне.
Смешанные системы счисления
К уже приведенному определению можно добавить теорему: “если P=Q n (P,Q,n – целые положительные числа, при этом P и Q — основания), то запись любого числа в смешанной (P-Q)-ой системе счисления тождественно совпадает с записью этого же числа в системе счисления с основанием Q.”
Смешанными системами счисления также являются, например:
1) Факториальная
2) Фибоначчиева
Перевод из одной системы счисления в другую
Иногда требуется преобразовать число из одной системы счисления в другую, поэтому рассмотрим способы перевода между различными системами.
Преобразование в десятичную систему счисления
Пример: 1012 = 1*2 2 + 0*2 1 + 1*2 0 = 4+0+1 = 510
Преобразование из десятичной системы счисления в другие
Записав все остатки снизу вверх, получаем итоговое число 17. Следовательно, 1510 = 178.
Преобразование из двоичной в восьмеричную и шестнадцатеричную системы
В качестве примера возьмем число 10012: 10012 = 001 001 = (0*2 2 + 0*2 1 + 1*2 0 ) (0*2 2 + 0*2 1 + 1*2 0 ) = (0+0+1) (0+0+1) = 118
Для перевода в шестнадцатеричную — разбиваем двоичное число на группы по 4 цифры справа налево, затем — аналогично преобразованию из 2-й в 8-ю.
Преобразование из восьмеричной и шестнадцатеричной систем в двоичную
Перевод из восьмеричной в двоичную — преобразуем каждый разряд восьмеричного числа в двоичное 3-х разрядное число делением на 2 (более подробно о делении см. выше пункт “Преобразование из десятичной системы счисления в другие”), недостающие крайние разряды заполним ведущими нулями.
Для примера рассмотрим число 458: 45 = (100) (101) = 1001012
Перевод из 16-ой в 2-ю — преобразуем каждый разряд шестнадцатеричного числа в двоичное 4-х разрядное число делением на 2, недостающие крайние разряды заполняем ведущими нулями.
Преобразование дробной части любой системы счисления в десятичную
Преобразование осуществляется также, как и для целых частей, за исключением того, что цифры числа умножаются на основание в степени “-n”, где n начинается от 1.
Преобразование дробной части двоичной системы в 8- и 16-ую
Перевод дробной части осуществляется также, как и для целых частей числа, за тем лишь исключением, что разбивка на группы по 3 и 4 цифры идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа.
Пример: 1001,012 = 001 001, 010 = (0*2 2 + 0*2 1 + 1*2 0 ) (0*2 2 + 0*2 1 + 1*2 0 ), (0*2 2 + 1*2 1 + 0*2 0 ) = (0+0+1) (0+0+1), (0+2+0) = 11,28
Преобразование дробной части десятичной системы в любую другую
Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в ноль и начать умножение получившегося числа на основание системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в ноль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль.
Для примера переведем 10,62510 в двоичную систему:
0,625*2 = 1,25
0,250*2 = 0,5
0,5*2 = 1,0
Записав все остатки сверху вниз, получаем 10,62510 = (1010), (101) = 1010,1012