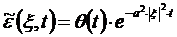На что влияют начальные условия приближения и каким образом их необходимо выбирать

Этап. Поиск начального приближения

Пусть x₁ = 1; F(1) = 0,1 – ln 1 = 0,1 >0; (a)

x₂ = 2; F(2) = 0,4 – 2* ln 2 2 –x*ln x = 0.

Для поиска решения выбираем метод, при котором последовательно, шаг за шагом, производится подстановка значений xв уравнение, а полученное на каждом шаге значение F(x) анализируется и уточняется. Вычисления производятся до тех пор, пока значение функции F(x) не приблизится к 0 с заданной точностью. Последнее значение x и будет искомым корнем уравнения. Такой метод широко используется в вычислительной математике и носит название метода итераций (последовательных приближений).

При сходящемся итерационном процессе для любого заданного положительного значения точности eps > 0 существует неравенство

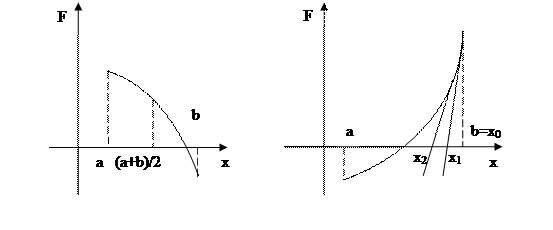
Отрезок [a,b] делится пополам и вычисляется значение функции в середине участка в точке (a+b)/2

F( (a+b)/2)=

При этом полученное значение функции может оказаться либо равным, либо не равным нулю. В первом случае, при F=0, середина отрезка x = (a+b)/2, и будет являться искомым корнем, обращающим функцию в нуль. Если значение функции в середине участка отлично от нуля, то надо определить знак этого значения и сравнить его со знаками функции в точке a и в точке b.

Теперь надо выбрать ту из половин отрезка [a,b], на концах которой функция приобретает значения с разными знаками, как обуславливалось при выборе первоначального отрезка [a,b]. Пусть

F(a) > 0, F(b) 0.

Тогда в качестве новых границ участка следует выбратьb и (a+b)/2, т.к. произведение функций от этих значений меньше нуля, что свидетельствует о наличии корня уравнения на выбранном участке. Обозначим границы нового отрезка, составляющего половину исходного, значениями [a₁, b₁].

Отрезок [a₁,b₁] делится пополам и вычисляется значение функции в середине участка в точке (a₁ + b₁)/2:

Теперь производится повторение анализа, выполненного при первой итерации. Если F((a₁+b₁)/2) = 0, то середина участка (a₁+b₁)/2 и является искомым значением корня, обращающим функцию в ноль. В противном случае вновь определяются знаки, которые принимает функция при подстановке в неё значений концов участка a₁ и b₁. Пусть

Тогда в качестве нового участка берётся та половина отрезка, у которой значения функции на её концах имеют разные знаки, т.е. половина отрезка с координатами b₁ и (a₁+b₁)/2. Обозначим эти значения как [a₂, b₂].

Третья итерация и, в случае необходимости, последующие итерации производятся аналогичным образом с использованием циклического алгоритма вычислений. В результате выполнения цикла вычислений на некоторой итерации длина очередного отрезка, полученного путём половинного деления, станет меньше заданной точности вычислений eps, т.е. начнет выполняться неравенство

Источник

Устойчивость решений ДУ по первому приближению

Пусть имеем систему дифференциальных уравнений

Разложим функции по формуле Тейлора по в окрестности начала координат:

Тогда исходная система (1) запишется так:

Вместо системы (2) рассмотрим систему

называемую системой уравнений первого приближения для системы (1).

Справедливы следующие предложения.

1. Если все корни характеристического уравнения

Говорят, что в случаях 1 и 2 возможно исследование на устойчивость по первому приближению.

В критических случаях, когда вещественные части всех корней характеристического уравнения (4) неположительны, причем вещественная часть хотя бы одного корня равна нулю, исследование на устойчивость по первому приближению, вообще говоря, невозможно (начинают влиять нелинейные члены ).

Пример 1. Исследовать на устойчивость по первому приближению точку покоя системы

Решение. Системы первого приближения

Нелинейные члены удовлетворяют нужным условиям: их порядок больше или равен двум. Составим характеристическое уравнение для системы (6):

Корни характеристического уравнения (7) вещественные и 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAADkAAAATBAMAAADYAbjmAAAAJ1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAB+jSoGAAAADHRSTlMAwB1kQYWh8DHg0VFNsKFOAAAA2ElEQVQoz2NgwA+YhbGLszSAqRwDrJJlkWBpHQFssuoGzEUgmvEQXIgjCc6MYWA4Crb4MEKHYwaMNZGBQRJEM51CMtBNBMo4yMAgA2bINCBJq0mDKSaQrAKIZRMA5CGkJ4OdDJJ1ADll+gQG1YUI3aqrkWUt204zKAWiyTJATWY+zXKMgQEhq7oYTBUyMIiDbDVgmK6AkFWDSDLkMDAANTED/RxjAJdVg/nIx4HlCAMDTwIw1ARgso4i8MgpNgeGPwfIcw5QWaSQZFA2QrAD8UVy43RhBpIBABPuJMc3pUukAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />. Следовательно, нулевое решение системы (5) неустойчиво.

Пример 2. Исследовать на устойчивость по первому приближению точку покоя систем

Решение. Точка покоя системы (8) асимптотически устойчива, так как для этой системы функция удовлетворяет всем условиям теоремы Ляпунова об асимптотической устойчивости. В частности,

Системы (8) и (9) имеют одну и ту же систему первого приближения

Характеристическое уравнение для системы (10)

имеет чисто мнимые корни, так что действительные части корней характеристического уравнения равны нулю.

Для системы первого приближения (10) начало координат является центром. Системы (8) и (9) получаются малым возмущением правых частей системы (10) в окрестности начала координат. Однако эти малые возмущения приводят к тому, что замкнутые траектории превращаются в спирали, в случае (8) приближающиеся к началу координат и образующие в точке устойчивый фокус, а в случае (9) — удаляющиеся от начала координат и образующие в точке неустойчивый фокус. Таким образом, в критическом случае нелинейные члены могут влиять на устойчивость точки покоя.

Пример 3. Рассмотрим замкнутый контур с линейными элементами (рис. 44); уравнение контура

Решение. Уравнение (11) эквивалентно системе

Рассмотрим систему первого приближения

Характеристическое уравнение для системы (13) имеет вид

Если \frac<4L>» png;base64,iVBORw0KGgoAAAANSUhEUgAAAFEAAAAsBAMAAADvHUkaAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAmIEBQRBl6MDRIDBRsUCjJh5DAAAB1ElEQVQ4y2NgoCIwNjYgQpUaAwPL////NxBUyPIJSBh9NCZsZDhIJccXIiwXBKm0LyaskOUKSKX/BcIqI0NAKvUTCKuUAfuon7DPuS+AVDJ/JxycFgtAKln+MjBwKSAJs+mhK2TOVFL8ocXABFTNhOzUOy8F0JUucXH76AoOznAkB3DX8PzGtN8EaJ79ZwbWiUhirN18/zAUsjr+OBoiX+cmDoklViUlJbUFQIeWYqjkUlLSegSUVoJ4iNX3x5HEj0C3HCAYGEzfGJjlE1i7CccExy8GBnkFxg27wdoO41EJSivzE2SVwIayaibjVukvwMD2l7ujowHibM1UnCr15fzEkWKLNVMVl8p+JfVq1FiUwq4QmFZYy9EiXBRELRREAqAgZAGGZT9KwmI+gakyARqc/w2IsR0YnCzIKplx+Yg5vtiA5T/rBLjX1XF53f///wus8xNheQUj5Jn3eDHsgjANgCUEyymYBCOaQlb1iZrapcQUXzunGDDcn0CEQu7KAAaG/QJEqAwHWWxPOOWC0i1IZQBhlVz/QYpYiLCc6S+xBTfHJ6JVgrNvArEquYgJJMZvQILXgQiVXOVAv4sR407m41OMPRKI8hKX+Hcp4jzPjKiKAKp5cVgk81juAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />, то начало координат также асимптотически устойчиво (все параметры положительны).

Асимптотическая устойчивость точки покоя видна из физических соображений: при положительном омическом сопротивлении с возрастанием ток неизбежно исчезает.

Устойчивость решений ДУ по отношению к изменению правых частей уравнений

Рассмотрим дифференциальные уравнения

Пример 4. В квадрате найти приближенное решение уравнения

Источник

Диффузионное приближение

К сожалению, во многих случаях на практике принципиально невозможно ограничиться только уравнениями равновесия на границе раздела. В этом случае переходят к приближениям более высокого порядка. В данной работе нет строгого доказательства возможности применения этого приближения, хотя в каждом из конкретных случаев приходится делать достаточно сложные оценки применимости этого приближения к реальной задаче.

Удобством диффузионного приближения является то, что в настоящее время в литературе рассмотрены все основные типы уравнений второго порядка практически для всех областей техники. При описании этих приближении авторы, как правило, опускают описание того, чем они пренебрегают при моделировании, если это опущено, то, скорее всего, задача решена в «типовой» постановке и включает следующие положения.

Основные положенияя типового диффузионного приближения.

1. Предположим, что все потоки в уравнениях (1.47) – (1.49) действуют независимо друг от друга ( ), например, в задаче тепломассопереноса передача тепла условно не зависит от передачи массы. Это приводит к тому, что общую систему уравнений можно разделить на отдельные системы более низкого порядка и решать отдельные задачи, которые часто решаются отдельно друг от друга (разными людьми). Связь между этими задачами осуществляется через граничные условия. Таким образом, например, если общая задача тепломассопереноса в одномерном приближении включает 27 уравнений вместе с граничными условиями, то отдельные задачи представляют собой систему из 1 уравнения в частных производных и 3 граничных условий.

2. Предположим, что на одной из границ выполняется закон локального равновесия фаз, т.е. потоки энергий слабые. Это позволяет решать данное уравнение в численном виде при достаточно простых методах построения сеток.

3. Предположим, что среда, в которой распространяются локальные потоки, однородна или квазиоднородна. Квазиоднородность предполагает, что существуют достаточно протяженные участки, в которых функции параметров (теплопроводность, теплоемкость, коэффициент диффузии, химические константы и т.д.) являются непрерывными функциями вместе со своими производными. Скачки могут происходить только на границе раздела.

4. Предположим, что на «удаленных» границах применимы стандартные граничные условия, которые ставятся из предположения, что потоки неразрывны по всем координатам.

Эти условия очень часто приводят к тому, что все уравнения приводятся к виду, обладающему следующими особенностями:

1. Задача упрощается за счет того, что обобщённые скорости потоков являются функциями только одной координаты, т.е. матрица коэффициентов Онсагера имеют линейную диагональную форму. В этом случае уравнения конвективного массопереноса представляют собой полилинейную форму, т.е. в декартовой системе координат Vx, Vy, Vz являются функцией только той координаты, по которой идет движение потока. В этом случае уравнение конвективного потока для скоростей по виду совпадает с уравнением переноса энергии.

2. Если процессы происходят с разной скоростью, то мы можем решать систему уравнений, а каждое уравнение независимо друг от друга. Эти решения связаны между собой только внутренними коэффициентами и граничными условиями. Таким образом, в декартовой системе координат 9 уравнений можно разбить по 3 уравнения, решаемые отдельно и связанные между собой граничными условиями.

Диффузионное приближение принято рассматривать в двух видах.

Первый вид представляет собой аналитическое решение типовых уравнений математической физики при постановке задач Коши и Дирихле. Рассмотрим простейший вид постановки такой задачи.

Аналитическое решение задачи теплопереноса.

Допустим, что существует передача какого-нибудь обобщенного потока, в частном случае, тепла. Мы можем воспользоваться решением типовой задачи распространения тепла в одном направлении в условиях, когда или границы распространения тепла лежат в бесконечности, или время распространения тепла является бесконечным (задача Коши, задача Дирихле). Такие задачи носят название «задачи с полубесконечными границами». Стоит заметить, что, как правило, время представляется в виде одной из координат.

Решение таких задач дается через фундаментальное решение оператора теплопроводности.

Фундаментальное решение оператора теплопроводности.

Рассмотрим фундаментальное решение оператора теплопроводности [7].

(2.19)

где δ(x, t) – дельта функции Дирака.

Решение этого уравнения выражается формулой:

(2.20)

Эта функция называется фундаментальным решением оператора теплопроводности.

Выведем формулу (2.20) методом преобразования Фурье. Для этого применим преобразование Фурье к равенству (2.19):

(2.21)

и воспользуемся формулами:

(2.22)

(2.23)

В результате для обобщённой функции получаем уравнение:

(2.24)

Пользуясь формулой с заменой на , заключаем, что решением уравнения (2.24) является функция:

Отсюда, применяя обратное преобразование Фурье и пользуясь формулой

получаем равенство (2.20):

Рассмотрим применение данного решения для различных граничных условий.

Задача Коши для уравнения теплопроводности.

1. Тепловой потенциал.

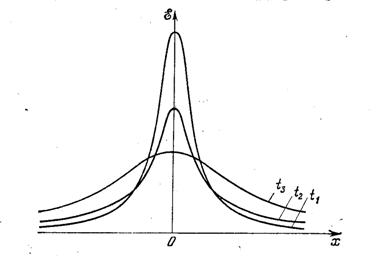
Рассмотрим поведение фундаментального решения в том случае, если источником обобщенного потока является точка заданной интенсивности θ(t):

(2.25)

Эта функция неотрицательна, обращается в нуль при , бесконечно дифференцируема при и локально интегрируема в .

, (2.26)

, в (2.27)

Рис. 2.1. График функции при различных

Фундаментальное решение даёт распределение потоков (в частности, температуры) от точечного мгновенного источника . Поскольку при всех и , то поток (тепло) распространяется с бесконечной скоростью. Но, вследствие диссипативных процессов, в реальности такое распространение потока не может быть осуществлено. Поэтому, такое решение может быть использовано только или в очень ограниченном диапазоне времени, или в очень узкой области. Чаще всего оно применяется для компенсации разрыва граничных условий в точках приложения сил или в области, где функции параметров (теплопроводность, теплоемкость, коэффициент диффузии, химические константы и т.д.) имеют разрыв.

В более общем случае, для получения аналитического решения потенциал потока (тепловой потенциал) определяется следующим образом.

Тепловой потенциал при наличии конечного источника излучения.

Допустим, существует источник излучения, имеющий форму и конечные размеры. Обозначим его обобщенной функцией f.

Пусть обобщённая функция обращается в нуль при . Обобщённая функция , где — фундаментальное решение оператора теплопроводности, называется тепловым потенциалом с плотностью .

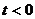
Если тепловой потенциал существует в , то он удовлетворяет уравнению теплопроводности:

(2.28)

Если обращается в нуль при , то тепловой потенциал заведомо существует в .

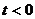
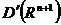
Выделим ещё один класс плотностей , для которых тепловой потенциал существует. Пусть — класс функций, обращающихся в нуль при и ограниченных в каждой полосе .

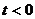
Если , то тепловой потенциал с плотностью существует в классе и выражается формулой:

(2.29)

2. Поверхностный тепловой потенциал.

Тепловой потенциал с плотностью называется поверхностным тепловым потенциалом (простого слоя с плотностью ),

Если — ограниченная функция в , то поверхностный тепловой потенциал существует в , принадлежит классу , представляется интегралом Пуассона:

(2.30)

3. Постановка задачи Коши для уравнения теплопроводности.

(2.31)

(2.32)

Считаем и . Предположим, что существует классическое решение этой задачи. Это значит, что , удовлетворяет уравнение (2.31) при и начальное условие (2.32) при .

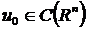
Продолжая функции и нулём при , заключаем, что продолженные функции и удовлетворяют в уравнению теплопроводности:

(2.33)

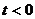
Обобщённой задачей Кошидля уравнения теплопроводности с источником назовём задачу о нахождении обобщённой функции , обращающейся в нуль при и удовлетворяющей уравнению теплопроводности

(2.34)

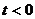
Уравнение (2.34) эквивалентно следующему:

Для любой справедливо равенство:

(2.35)

Из уравнения (2.34) следует, что необходимым условием разрешимости обобщенной задачи Коши является обращение в нуль при .

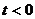
4. Решение задачи Коши.

Пусть 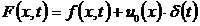, где и — ограниченная функция в . Тогда решение соответствующей обобщённой задачи Коши существует и единственно в классе и представляется формулой Пуассона:

(2.36)

Таким образом, общее решение распределения интересующего нас потока по координате и времени в аналитическом диффузионном приближении может быть представлено в виде двух функций, одна из которых характеризует форму потока в начале координат, вторая характеризует изменения потока во времени, f(x, t)и θ(t) определяются из общей постановки задачи и индивидуальны для каждого потока.

Во многих случаях, решение можно представить в виде сумы конечного ряда:

, (2.37)

где Ф(x, t) – интеграл ошибок.

В более сложных случаях решение может быть выражено в виде бесконечных рядов, полиномов Лежандра, функции Бесселя, Ханкеля или других специализированных функций. Однако такое представление выходит за рамки нашего курса.

Численное решение уравнений переноса в диффузионном приближении.

В тех случаях, когда среду нельзя представить в виде уравнений с постоянными коэффициентами, или граничные условия нельзя представить в виде среды с бесконечно распространяющимися потоками, используют более сложную форму.

, (2.38)

где — удельная емкость исследуемого потока (теплоёмкость),

— удельная проводимость исследуемого потока (теплопроводность),

— источник потока,

— коэффициент связывающей скорость прохождения потока в веществах, имеющих различные свойства (коэффициент теплопроводности),

— скорость переноса потока.

Во многих случаях, применим набор граничных условий, который позволяет, не выясняя, что происходит на удаленных границах, ставить задачу, которая описывает процесс с качеством, достаточным для наших целей. Такая постановка особенно важна в случае моделирования процессов проходящих при высоких температурах, давлении или в средах, имеющих высокую степень агрессивности, где затруднено непосредственное измерение параметров.

В этих случаях можно предположить, что:

1. Потоки на невзаимодействующих границах просто отражаются от стенки. Такое приближение называется «зеркально отражающая граница». В этом случае предполагается, что мы можем поставить следующие граничные условия:

, (2.39)

t_гр – время за которое поток достигает границы.

2. Все потоки на удаленной границе равны нулю – абсолютное поглощение.

=0 (2.40)

В этом случае уравнение решается численно с помощью достаточно простых сеточных методов. Однако граничные условия на взаимодействующей границе лучше выбирать, используя решение в аналитическом приближении в узкой области у границы раздела.

В этом случае аналитическое решение изменяется вместе с изменением входных параметров и применимо как граничное условие для более точного решения.

Источник