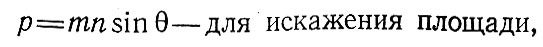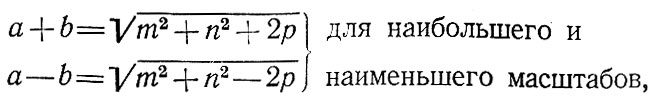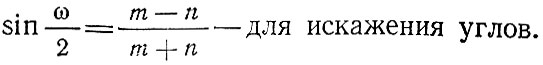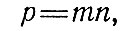На картах встречаются искажения чего
Иллюзии мозга. Картографические проекции

Искажения площадей в проекции Меркатора
На самом деле Африка по площади больше, чем США, Китай, Индия и почти вся Европа, вместе взятые. Но из общепринятых проекций географических карт складывается иллюзия, что это не так. Так называемая проекция Меркатора, которая используется для многих карт, сильнее всего искажает площади ближе к полюсам. Небольшая Гренландия (площадь меньше Конго) кажется гигантской территорией. Антарктида тоже. Площадь России значительно преувеличена относительно южных стран. Или взять Украину, площадь которой на самом деле равняется площади Мадагаскара.
Все карты мира врут нам уже много столетий. Более того, в разных странах — России, Европе, США, Китае, Австралии, Чили, Южной Африке — карты мира очень сильно отличаются.
Искажения на картографических картах — вполне естественное явление, потому что картографам нужно сделать развёртку эллипсоида Земли на плоскости. Это в принципе невозможно сделать без искажений. Вопрос только в то, что именно можно искажать, а что нельзя.
Искажения бывают четырёх видов:

Истинный размер Африки в сравнении с разными странами. Автор карты: Кай Краузе
Почему большинство людей не осознают истинный масштаб гигантской Африки или более скромные размеры России, Канады или Гренландии? Потому что по какой-то причине проекция Меркатора используется не только в морской навигации, но и во многих других географических картах. По этим картам учат в школах, такие карты показывают по телевизору. Отсюда и характерное когнитивное искажение у многих обывателей.
Главное, что нам совсем необязательно пользоваться в повседневной жизни проекцией Меркатора. Мы же не морские навигаторы и не планируем авиационных налётов на соседние страны, куда нужно лететь по прямой. Мы простые мирные люди. Зачем нам совершенное точное направление по прямой линии между географическими точками? Если пофантазировать, то в обычной жизни это может быть удобно только при планировании больших путешествий на автомобиле на несколько тысяч километров. В остальных случаях мало кто перемещается на собственном транспорте. В основном, люди пользуются самолётами и поездами, так что даже у путешественников не нужды прокладывать маршрут самостоятельно.
Почему же тогда проекция Меркатора используется в школьных картах, на телевидении и т.д.? Это не совсем понятно. Возможно, для современного обывателя всё-таки более важно понимать сравнительные размеры стран мира, а не определять прямые направления по маршрутам.
Как мы уже заметили, в проекции Меркатора реальные площади показаны только возле экватора, и все остальные площади на земном шаре очень сильно искажаются. Эти искажения — цена, которую мы платим за знание точных направлений при навигации.
Как же нам составить более точную и справедливую карту мира с наименьшими искажениями площадей? В 2009 году эту проблему попытались решить дизайнеры из компании AuthaGraph. Их работа заключается в применении геометрических идей моделирования к практическим задачам. Одна из этих задач — проектирование более наглядной карты мира. Тогда они и составили карту AuthaGraph World Map, которая наиболее справедливо отображает площади географических стран и территорий.
Здесь используется разновидность так называемой изометрической проекции, при которой в отображении трёхмерного объекта на плоскость коэффициент искажения (отношение длины спроецированного на плоскость отрезка, параллельного координатной оси, к действительной длине отрезка) по всем трём осям один и тот же.
Проекция составлена в несколько этапов. Сначала эллиптическая поверхность земного шара разделена на 96 равных треугольников. Они спроецированы на 96 регионов модифицированного тетраэдра. Затем тетраэдр «сплющен» до правильной формы и обрезан, чтобы его можно было развернуть в прямоугольную форму, то есть в стандартную прямоугольную плоскую карту привычной формы.

Этапы составления проекции AuthaGraph World Map
Конечно, можно было сразу спроецировать сферу на тетраэдр обычным оптическим способом, но при этом возникают сильные искажения, которые бросаются в глаза. Идея предварительного разбиения на 96 регионов была в том, чтобы минимизировать такие искажения и сохранить пропорции территорий друг относительно друга.
Но нет предела совершенству. На основе оригинальной карты AuthaGraph японский дизайнер Хадзимэ Нарукава (Hajime Narukawa) создал новый вариант, который великолепно смотрится и при этом так же сохраняет пропорции стран и континентов друг относительно друга, а также соотношение земной массы и Мирового океана.

Карта Хадзимэ Нарукавы на основе AuthaGraph World Map
Эту более справедливую и пропорциональную карту можно использовать и в школьных учебниках, и в средствах массовой информации, поскольку она более точно показывает на плоскости проекцию земного шара и даёт лучшее представление о том, как выглядит наша Земля. Её преимущество ещё и в том, что на ней все континенты показаны без разрыва карты, включая Антарктиду (ну и конечно Япония находится в центре, как на многих японских картах: это вполне нормально, на российских картах тоже вертикальная ось мира проходит через Москву). И ещё несколько таких карт сшиваются в единое пространство, так что можно наглядно представить взаимное расположение континентов. Здесь понятно, например, какая точка европейской России ближе всего к Аляске.
Все существующие географические карты — это искажения. Самую точную картину мира показывает только глобус. Но если мы вынуждены использовать плоские поверхности, то хотя бы постараемся минимизировать количество искажений.
На картах встречаются искажения чего
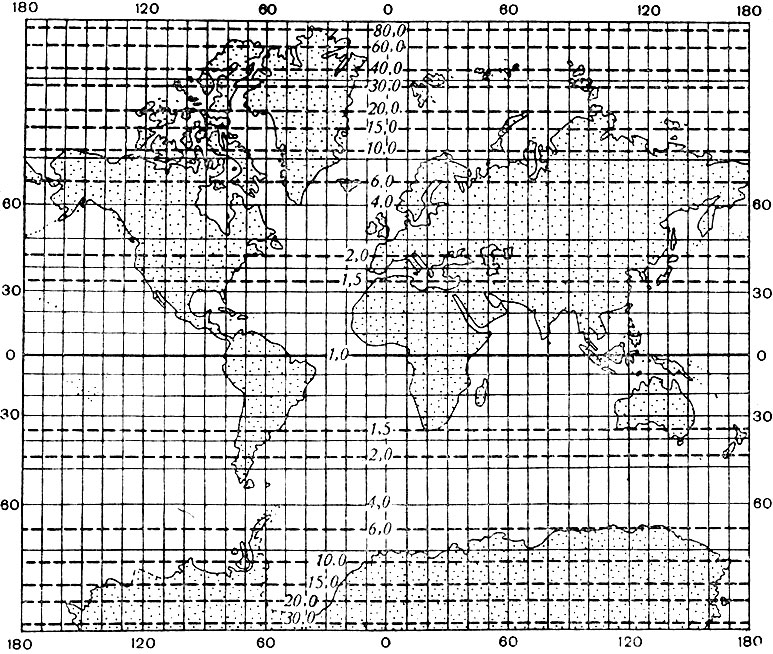
Рис. 2.13. Изоколы площадей в равноугольной цилиндрической проекции Меркатора
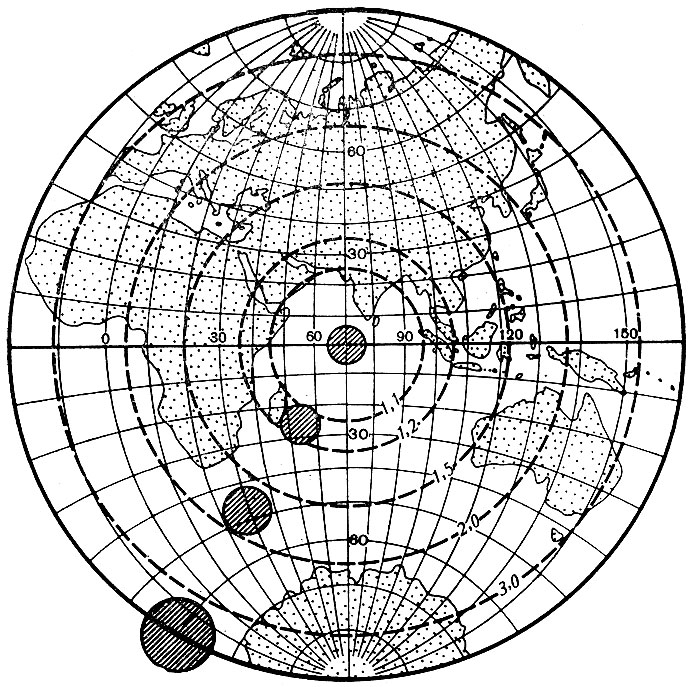
Рис. 2.14. Картографическая сетка в экваториальной стереографической проекции с изоколами площадей
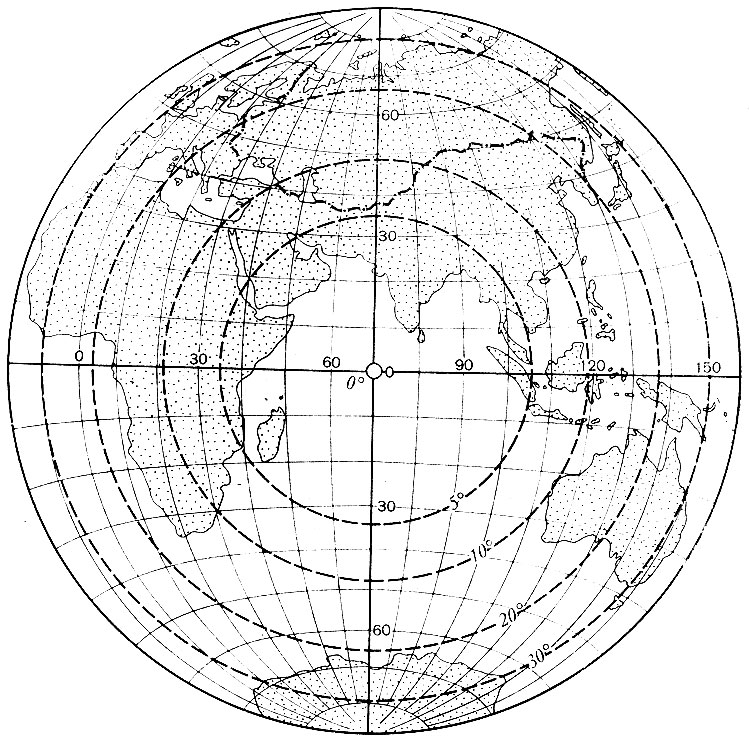
Также легко представить расположение изокол в поперечных и косых проекциях. Например, в поперечной цилиндрической проекции изоколы параллельны меридиану касания, и, следовательно, такие проекции выгодны для передачи территорий, вытянутых вдоль этого меридиана с севера на юг. В любой азимутальной проекции изоколы образуют окружности, концентрические относительно точки касания плоскости (рис. 2.14 и 2.15); поэтому азимутальные проекции удобны для территорий округлой формы (при центральном положении точки касания). В произвольных проекциях изоколы могут образовывать сложную систему кривых линий (см. рис. 2.8). В математической картографии доказывается, что при изображении конкретных территорий наименьшие искажения обеспечиваются проекциями, у которых изоколы по своей форме близки к общему контуру картографируемой территории.
Важно знать, что при наличии картографической сетки величина искажений может быть определена на любом участке карты, еслв даже проекция не указана.
Рис. 2.15. Картографическая сетка в экваториальной равновеликой азимутальной проекции (Ламберта) с изоколами углов
Для этого достаточно определить в соотвествующем месте карты масштабы по меридиану и параллели т и п, а также угол θ между меридианом и параллелью. Для нахождения величин т и п следует: а) измерить дуги меридиана и параллели возле соответствующей узловой точки картографической сетки; б) определить масштаб по меридиану и параллели посредством деления полученных величин на длины соответствующих дуг эллипсоида (заимствуемые из картографических таблиц). Найти величины т и п посредством деления масштабов по меридиану и параллели на главный масштаб. Угол θ между меридианом и параллелью измеряется транспортиром.
Для вычисления по величинам т, п и углу θ значений а, b, р, и угла θ математическая картография дает следующие несложные формулы:
(2.4)
(2.5), (2.6)
(2.7)
Если главные направления совпадают с меридианами и параллелями, т. е. когда меридианы и параллели сетки взаимно перпендикулярны, то а=т, b=п (или а=п, b=т) и формулы приобретают вид
(2.8)
Ответьте на вопрос! Какие искажения бывают на карте?
При изображении поверхности Земли на плоскости, т. е. на карте, возникают четыре вида искажений, которые называются искажениями длины, площади, угла и формы.
Искажаются длины линий, углы, площади и формы географических объектов. Искажения на карте тем больше, чем большая изображаемая на ней поверхность. На планах местности и крупномасштабных картах, изображающих небольшие участки местности, искажений почти нет, но на мелкомасштабных картах они бывают очень велики. А отсюда и неодинаковый масштаб длин и площадей в разных местах карты.
Изображая земную поверхность на карте, приходится учитывать кривизну Земли и выбирать ту или другую картографическую проекцию, которая позволяет избежать одного из искажений или ослабить другое.
В зависимости от характера и размеров искажений проекции делятся на равноугольные, равновеликие и произвольные.
Равноугольные проекции хранят без искажений углы и формы малых объектов, однако в них сильно деформируются длины линий и площади объектов. За картами, созданными в равноугольные проекции, удобно прокладывать маршруты судов и самолетов, поскольку измеренные на таких картах углы точно соответствуют углам на местности, которые могут фиксироваться приборами.
Равновеликие проекции не искажают площадей, однако формы объектов и углы у них сильно искажены.
Произвольные проекции имеют все виды искажений, но они распределяются на карте наиболее выгодным образом. Например, существуют проекции с минимальными искажениями в центральной части, зато они резко возрастают на краях карты.
Лекция №3 картографические искажения
Сферическая поверхность Земли при ее изображении на карте не может быть совмещена с плоскостью без разрывов или перекрытий. Для создания непрерывного картографического изображения приходится прибегать к растяжениям или сжатиям его частей. Это в свою очередь приводит к нарушениям геометрических свойств изображенной поверхности, т. е. к ее искажению.
Картографическим искажением называют нарушение геометрических свойств участков земной поверхности и расположенных на них объектов при их изображении на плоскости. Искаженными могут быть длины линий, горизонтальные углы между определенными направлениями, формы и размеры площади, занимаемой участком или объектом. Поэтому можно говорить о четырех видах картографических искажений: длин линий, углов, форм и площадей.
Искажение длин линий (расстояний) связано с изменением масштаба длин на одной и той же карте и выражается, в частности, в том, что расстояния, одинаковые на уровенной поверхности Земли, изображены на этой карте отрезками разной длины. Масштаб, величина которого отлична от главного масштаба карты, называют частным масштабом.
Судить о наличии на карте искажения длин удобно путем сравнения величины отрезков меридианов между соседними параллелями. Если они повсеместно равны, то искажения длин по меридианам нет, если такого равенства нет (на рисунке 3 отрезки АВ и CD), то искажение длин линий имеется: Если карта отображает такую большую территорию, что на ней показаны и экватор и параллель 60° широты, то нетрудно по ней установить, имеется ли искажение длин вдоль параллелей. Для этого достаточно сравнить длину отрезков экватора и параллели с широтой 60° между соседними меридианами. Известно, что параллель 60° широты в два раза короче экватора. Если таково же соотношение указанных отрезков на карте, то искажения длин по параллелям нет; в противном случае оно имеется.
Искажение углов состоит в том, что углы на карте между взятыми направлениями не равны горизонтальным углам между теми же направлениями на поверхности земного эллипсоида. Очень просто установить по карте, искажены ли у нее углы пересечения меридианов и параллелей по отклонению их от прямого угла.
Искажение форм состоит в том, что форма участка или занятой объектом территории на карте отлична от их формы на уровенной поверхности Земли. Наличие искажения этого вида на карте можно установить путем сопоставления формы клеток картографической сетки, расположенных на одной широте: если они одинаковы, то искажения нет. На рисунке две заштрихованные клетки различием формы свидетельствуют о наличии искажения данного вида. Можно также выявить искаженность формы определенного объекта (материка, острова, моря) по соотношению его ширины и длины на анализируемой карте и на глобусе. Например, на карте полушария ширина полуострова Камчатка укладывается вдоль ее длины (от мыса Лопатка на юге до параллели 60° с. ш.) более трех раз, тогда как на глобусе это отношение равно 1:2.
Четвертый вид картографического искажения — искажение площадей связан с масштабом площади: при постоянстве величины масштаба площади по всей поверхности карты искажения площадей на ней нет. Простой способ выявления искаженности этого вида состоит в сравнении площадей клеток картографической сетки, ограниченных одноименными параллелями: при равенстве площадей клеток искажения нет. Это имеет место, в частности, на карте полушария, на которой заштрихованные клетки различаются по форме, но имеют одинаковую площадь.
Анализируя искаженность карты, можно не только установить наличие или отсутствие картографического искажения того или иного вида, но и измерить величины этих искажений. Такую задачу решают, вычислив показатели искажений.
Искажение длин, к примеру, тем более, чем сильнее частный масштаб в данном месте карты по данному направлению отличается от главного масштаба. Поэтому за показатель искажения длин принимают отношение этих масштабов. Сам показатель обозначают греческой буквой μ: μ=частный масштаб/главный масштаб
Из формулы видно, что показатель искажения длин выражается отвлеченным числом, целым или дробным. Он может быть больше или меньше единицы; при равенстве частного и главного масштабов показатель равен 1.
Для вычисления показателя μ требуется узнать величину частного масштаба в данном месте карты; главный масштаб обычно на ней подписан. Вычисление проще проводить вдоль линий картографической сетки, при этом масштаб узнают из сравнения измеренной на карте длины отрезка меридиана или параллели с их длиной на поверхности земного эллипсоида (взятой из таблиц).
К примеру, длина отрезка среднего меридиана физической карты восточного полушария в атласе для 6-го класса на участке между параллелями 60° и 70° с. ш. равна 10,4 мм. Истинная длина этого отрезка меридиана равна (с округлением) 1115 км (111,5 км × 10). Соответственно, частный масштаб равен 10,4 м: 1115 км = 1:107 200 000. Главный масштаб карты 1:90 000 000, следовательно, μ= 1:107 200 000:1:90 000 000 = 0,84.
Значение вычисленного показателя искажения длин меньше 1, что свидетельствует о сжатии данного участка меридиана сравнительно с неискаженными его частями. На «растянутых» участках карты показатель был бы больше 1.
Показатель искажения длин μ имеет особые обозначения, если он направлен по меридиану (m), по параллели (n). Самый большой показатель искажения длин у данной точки обозначают латинской буквой α, а наименьший — буквой b. Сами же взаимно перпендикулярные направления, по которым действуют наибольший и наименьший показатели искажения длин, называют главными направлениями.
За показатель искажения углов между линиями картографической сетки принимают величину отклонения их от 90° и обозначают его греческой буквой ε (эпсилон). ε = θ — 90°, где θ(тэта) — измеренный на карте угол между меридианом и параллелью. Угол θ равен 115°, следовательно, ε = 25°.
В точке, где угол пересечения меридиана и параллели остается на карте прямым, углы между другими направлениями могут быть измененными на карте, поскольку в каждой данной точке величина искажения углов может изменяться с переменой направления.
За общий показатель искажения углов ω (омега) принимают наибольшее искажение угла в данной точке, равное разности его величины на карте и на поверхности земного эллипсоида (или шара). При известных показателях ɑ и b величину ω узнают по формуле
Показатель искажения площадей (р) вычисляют как произведение наибольшего и наименьшего показателей искажения длин в данном месте карты: р = а×Ь.
Главные направления в данной точке карты могут совпадать с линиями картографической сетки, но могут с ними не совпадать. Тогда показатели ɑ и b по известным тиn вычисляют по формулам
Картографическая проекция определяет переход от сфероидической поверхности, к плоскости и позволяет учитывать неизбежные при этом нарушения геометрических свойств объектов, т. е. искажения.
Входящий в уравнения показатель искажения р узнают в этом случае по произведению: p = m-n-cos ε
Показатель искажения форм (k) зависит от различия наибольшего (а) и наименьшего (Ь) показателей искажения длин в данном месте карты и выражается формулойK= ɑ /b

Виды искажений и их величину в конкретном месте карты можно наглядно отобразить с помощью эллипсов искажений. Эллипсами искажений называют изображенные на карте геометрические фигуры (эллипсы или круги), формы и размеры которых соответствуют видам и величине искажений, имеющихся в центральной точке фигуры.
Из теории картографических проекций (рис) известно, что на карте полушарий расположенная в центре точка пересечения среднего меридиана 70° в. д. с экватором не имеет искажения. Поэтому эллипс искажений в этом месте карты имеет форму круга с условно принятым радиусом (например, 5 мм). Выше был вычислен показатель искажения длин на среднем меридиане карты на участке между параллелями 60° и 70° с. ш. Он оказался равным 0,84. При построении эллипса искажений в этом месте карты его радиус по меридиану приходится уменьшать и брать равным 5 мм X0,84 = 4,2 мм. Радиус эллипса искажений, перпендикулярный меридиану, т. е. направленный вдоль параллели, имеет размер 5,7 мм, потому что вычисленный показатель искажения длин n равен 1,14 (при частном масштабе длины, равной 6,6 мм:472 км = = 1:78 700 000).
Сравнивая эллипс, построенный в этом месте карты, с неискаженным эллипсом, можно установить следующее: а) масштабы длин по разным направлениям различны, причем вдоль меридиана показатель искажения длин наименьший, т. е. m = b, тогда как по параллели он наибольший n = а; б) форма эллипса искажения не круг, что свидетельствует об искажении форм; в) площадь эллипса искажений равна площади эллипса в неискаженной центральной точке карты, т. е. искажения площадей здесь нет (это же подтверждает произведение а×Ь = р, примерно равное 1).
Изменение величины искажений с переходом от одного участка карты к другому показывают с помощью изокол или линий, по всей длине которых величина искажений данного вида не изменяется. Часто изоколы имеют вид пунктирных линий, в разрыве или возле которых указан показатель искажения. Для определения (учета) искажений используют также номограммы или таблицы искажений, вычисленных заранее для узловых точек.
Величина искажений на разных географических картах зависит от охвата изображенной территории и от способа построения математической основы карты. С увеличением охвата территории искаженность карты обычно увеличивается: на картах материков и океанов она, как правило, больше, чем на картах частей материков или на морях. Еще большие искажения имеют карты полушарий и мировые карты. Здесь отметим, что у многих карт размеры искажений увеличиваются в их краевых и уменьшаются (или отсутствуют) в средних частях. Точки или линии на карте, в которых искажений нет, называют точками или линиями нулевых искажений
Картографические проекции и искажения на картах
Поверхность земного шара нельзя изобразить на плоскости без искажений. Только на шарообразном глобусе можно сохранить подобие и пропорциональность размеров всех частей земной поверхности. Но глобусы неудобны для пользования, и масштаб их обычно не бывает крупным, например, при масштабе 1 км в 1 см (1 : 100 000) диаметр глобуса был бы равен 127.4 м.
Существуют различные способы изображения земной поверхности на плоскости. Все они называются картографическими проекциями. Некоторые из них получаются действительно проектированием земной поверхности на плоскость лучами, исходящими из постоянной точки зрения, расположенной вне, на или внутри земного шара, другие имеют иной геометрический смысл. Каждый из этих способов указывает вполне определенный метод изображения земной поверхности на плоскости и учет неизбежных искажений.
Впрочем, если взять обычный школьный глобус 1 : 50 000 000 масштаба (диаметр которого около 25 см) и приколоть к его поверхности небольшой листок бумаги размером в 1 см2, то окажется, что он без складок почти полностью совпадает с поверхностью глобуса. Это показывает, что на небольших площадях мы можем считать земную поверхность плоской и изображать ее на бумаге с сохранением геометрического подобия фигур. Такие изображения часто называются планами. Применение проекций теряет здесь свое значение, так как даже в разных, но надлежаще выбранных, проекциях изображения очень малых участков земного шара почти не различаются между собой.
При рассмотрении картографических проекций изображение на плоскости земной поверхности практически заменяется изображением на плоскости географической сетки меридианов и параллелей, которая на карте получает название картографической сетки. Это допустимо потому, что, построив на карте меридианы и параллели, мы можем нанести любую точку по ее географическим координатам. Поэтому в последующем изложении речь идет о сетке меридианов и параллелей на «математической поверхности» земли, за которую мы принимаем поверхность океанов, мысленно продолжаемую под материками, и об изображении этой сетки на плоскости. Для некоторых проекций картографические сетки строятся геометрическим путем, но чаще используют другой прием. Сперва вычисляют по имеющимся формулам выбранной проекции плоские прямоугольные координаты точек пересечений меридианов и параллелей, затем по координатам накладывают эти точки на бумагу и далее соединяют их плавными кривыми линиями, изображающими меридианы и параллели.
Каждому условному изображению земной поверхности на плоскости, т. е. каждой проекции соответствует вполне определенный вид картографической сетки и вполне определенные допускаемые искажения. Различают искажения длин, площадей и углов.
Известно, что на земной поверхности все меридианы имеют одинаковую длину; также равны между собой отрезки одной и той же параллели между соседними меридианами. Но только средний меридиан изображается прямой линией; остальные меридианы — кривые линии, длина которых возрастает по мере удаления от среднего меридиана. В той же степени искажаются и параллели — отрезки их между соседними меридианами увеличиваются с удалением от среднего меридиана.
Существуют другие проекции, которые не искажают длины вдоль некоторых, вполне определенных, направлений. Например, равнопромежуточная цилиндрическая. На ней меридианы переданы без искажений, так как длины меридианов на сетке равны длинам меридианов в натуре, разумеется, с уменьшением до масштаба карты. Но длины параллелей в этой проекции искажены. На сетке отрезки параллелей между двумя соседними меридианами остаются постоянными на любой широте, тогда как в натуре они уменьшаются по мере приближения к полюсам.
Выражение «искажение длин» означает, что длины передаются на одной и той же карте с различным уменьшением, т. е. в различных масштабах в разных местах карты. Другими словами, масштаб на одной и той же карте не представляет собой постоянной величины; он может меняться не только в различных точках, но даже в одной точке по различным направлениям.
Масштаб, который подписывается на карте, называется главным, он определяет отношение длин на карте к соответствующим длинам в натуре лишь в некоторых, определенных для каждой проекции, частях карты. Масштабы в остальных ее частях больше или меньше главного и называются частными.
Такая проекция, которая передавала бы без искажений любые длины по любому направлению, невозможна, так как она сохраняла бы подобие и пропорциональность всех частей земной поверхности, что может иметь место только на глобусе.
Искажения площадей можно проследить на тех же рисунках. Поверхности клеток, расположенных между двумя соседними параллелями, имеют в натуре одинаковую величину, но они заметно возрастают к востоку и западу от среднего меридиана. Поверхности клеток, ограниченных двумя меридианами, в натуре уменьшаются к северу и югу от экватора; но все они имеют одинаковую величину.
Однако существуют многочисленные проекции, на которых величины поверхностей передаются без искажений, все площади на таких картах пропорциональны величинам соответствующих поверхностей в натуре, хотя подобие фигур нарушено. Такие проекции называются равновеликими, равноплощадными или эквивалентными.
Изображение полосы местности вдоль меридиана в различных равноугольных проекциях
Меридианы и параллели, образующие между собой в натуре прямые углы, сохраняют перпендикулярность только вдоль среднего меридиана. Наоборот, картографическая сетка свободна от искажений углов. Такие проекции, которые сохраняют величину углов, называются равноугольными или конформными. Вокруг каждой точки равноугольной проекции на бесконечно малых расстояниях масштаб можно считать постоянным.
Существует множество проекций, которые не являются ни равновеликими, ни равноугольными (их называют произвольными), но нет такой, которая совмещала бы в себе оба качества.