На плоскости отметили 20 точек известно что никакие три
На плоскости отметили 20 точек известно что никакие три
Задача 1:
Из класса, в котором учатся 30 человек, нужно выбрать двоих школьников для участия в математической олимпиаде. Сколькими способами это можно сделать?
Решение:
Первого ученика можно выбрать 30 способами, второго, независимо от выбора первого ученика, – 29 способами. При этом каждая пара учитывается дважды. Поэтому ответ: 30 29/2 = 435 способов.
Задача 2:
Сколькими способами можно выбрать команду из трех школьников в классе, в котором учатся 30 человек?
Решение:
Первого ученика можно выбрать 30 способами, второго – 29 способами, третьего – 28 способами. Таким образом получаем 30 29 28 вариантов выбора. Однако каждая команда при этом подсчете учтена несколько раз: одна и та же тройка учеников может быть выбрана по разному, например, сначала А, потом В, потом С или сначала С, потом А, потом В и т.д. Поскольку число перестановок из трех элементов равно 3!, то каждая команда учтена нами ровно 3! = 6 раз. Поэтому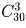 
равно (30 29 28)/3!.
Задача 3:
Сколькими способами можно выбрать 4 краски из имеющихся 7 различных?
Решение:
.
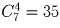
Задача 4:
У одного школьника есть 6 книг по математике, а у другого – 8. Сколькими способами они могут обменять три книги одного на три книги другого?
Решение:
Первый школьник может выбрать 3 книги для обмена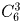 
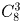
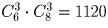
способами, второй – 
способами. Таким образом, число возможных обменов равно 
.
Задача 5:
В шахматном кружке занимаются 2 девочки и 7 мальчиков. Для участия в соревновании необходимо составить команду из четырех человек, в которую обязательно должна входить хотя бы одна девочка. Сколькими способами это можно сделать?
Решение:
В команду входит либо одна девочка, либо две. Разберем оба случая. Если в команде две девочки, то двух мальчиков к ним можно добавить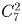 
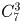
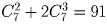
способами. Если же в команду входит только одна девочка (ее можно выбрать двумя способами), то команду можно дополнить тремя мальчиками 
различными способами. Таким образом, общее число возможных команд равно 
.
Задача 6:
Сколькими способами можно разбить 10 человек на две баскетбольные команды по 5 человек в каждой?
Решение:
Первую команду можно выбрать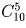 
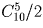
способами. Этот выбор полностью определяет вторую команду. Однако при таком подсчете каждая пара команд А и В учитывается дважды: один раз, когда в качестве первой команды выбирается команда А, и второй, – когда в качестве первой команды выбирается команда В. Таким образом, ответ: 
.
Задача 7:
На плоскости отмечено 10 точек так, что никакие три из них не лежат на одной прямой. Сколько существует треугольников с вершинами в этих точках?
Решение:
.
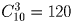
Задача 8:
Рота состоит из трех офицеров, шести сержантов и 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из офицера, двух сержантов и 20 рядовых?
Решение:
(n 8 + 1)(n 8 – 1) = n 16 – 1 = 0 (mod 17).
Задача 9:
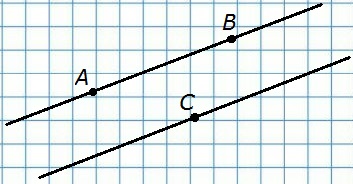
На прямой отмечено 10 точек, а на параллельной ей прямой – 11 точек. Сколько существует а) треугольников; б) четырехугольников с вершинами в этих точках?
Решение:
а)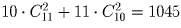 
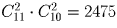
б) 
.
Задача 10:
Сколькими способами можно выбрать из 15 различных слов набор, состоящий не более чем из 5 слов?
Решение:
.
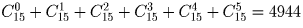
Задача 11:
Сколькими способами можно составить комиссию из 3 человек, выбирая ее членов из 4 супружеских пар, но так, чтобы члены одной семьи не входили в комиссию одновременно?
Решение:
Выберите сначала семьи, а потом в каждой паре конкретного представителя. Ответ: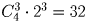 
.
Задача 12:
В классе, в котором учатся Петя и Ваня – 31 человек. Сколькими способами можно выбрать из класса футбольную команду (11 человек) так, чтобы Петя и Ваня не входили в команду одновременно?
Решение:
Разберите три случая: в команду входит только Петя; в команду входит только Ваня; оба они в команду не входят. Ответ: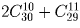 
.
Задача 13:
Сколькими способами можно переставить буквы слова «ЭПИГРАФ» так, чтобы и гласные, и согласные шли в алфавитном порядке?
Решение:
Все определяется местами, на которых стоят гласные буквы. Ответ: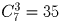 
.
Задача 14:
Из 12 девушек и 10 юношей выбирают команду, состоящую из пяти человек. Сколькими способами можно выбрать эту команду так, чтобы в нее вошло не более трех юношей?
Решение:
.
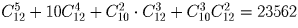
Задача 15:
Сколькими способами можно расставить 12 белых и 12 черных шашек на черных полях шахматной доски?
Решение:
.
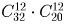
Задача 16:
а) Сколькими способами можно разбить 15 человек на три команды по 5 человек в каждой?
б) Сколькими способами можно выбрать из 15 человек две команды по 5 человек в каждой?
Решение:
а) 
; б) 
.
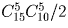
Задача 17:
Сколькими способами можно выбрать из полной колоды (52 карты) 10 карт так, чтобы
а) среди них был ровно один туз?
б) среди них был хотя бы один туз?
Решение:
а)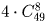 
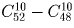
; б) Перейдите к дополнению. Ответ: 
.
Задача 18:
Сколько существует 6-значных чисел, у которых по три четных и нечетных цифры?
Решение:
Разберите случаи в соответствии с тем, цифра какой четности стоит на первом месте. Затем в каждом случае выберите места для нечетных цифр. Ответ: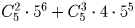 
.
Задача 19:
Сколько существует 10-значных чисел, сумма цифр которых равна а) 2; б) 3; в) 4?
Решение:
Разберите все возможные представления чисел 2, 3, 4 в виде суммы нескольких натуральных слагаемых. Не забывайте, что первая цифра – не ноль. Ответ: а) 10; б)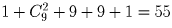 
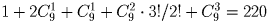
; в) 
.
Задача 20:
Человек имеет 6 друзей и в течение 5 дней приглашает к себе в гости каких-то троих из них так, чтобы компания ни разу не повторялась. Сколькими способами он может это сделать?
Решение:
.
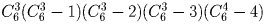
Задача 21:
Как известно, для участия в лотерее «Спортлото» нужно указать шесть номеров из имеющихся на карточке 45 номеров.
а) Сколькими способами можно заполнить карточку «Спортлото»?
б) После тиража организаторы лотереи решили подсчитать, каково число возможных вариантов заполнения карточки, при которых могло быть угадано ровно три номера. Помогите им в этом подсчете.
Решение:
а)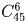 
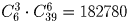
; б) 
.
Волжский класс
Боковая колонка
Рубрики
Видео
Книжная полка
Малина для Админа
Боковая колонка
Опросы
Календарь
| Пн | Вт | Ср | Чт | Пт | Сб | Вс |
|---|---|---|---|---|---|---|
| « Ноя | ||||||
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 | ||
5 класс. Математика. Никольский. Учебник. Ответы к стр. 80
Измерение величин
Прямая. Луч. Отрезок
Ответы к стр. 80
346. Проведите прямую AB и вне ее точку C. Через точку C проведите прямую параллельную прямой AB.
347. Сколько прямых можно провести через одну точку?
348. Даны три точки, не лежащие на одной прямой. Через каждые две точки проведена прямая. Сколько прямых проведено?
349. Даны четыре точки так, что никакие три из них не лежат на одной прямой. Через каждые две точки проведена прямая. Сколько прямых проведено?
350. На сколько частей прямая делит плоскость?
351. На сколько частей делят плоскость две прямые, если они:
а) пересекаются; б) параллельны?
а) на 4 части;
б) на 3 части.
352. На сколько частей можно разделить плоскость тремя прямыми?
Если прямые параллельны — на 4 части, если пересекаются в одной точке — на 6 частей, если пересекаются не в одной точке — на 7 частей.
353. Отметьте на листе бумаги точку, проведите несколько лучей с началом в этой точке. Сколько таких лучей можно провести?
354. Отметьте на прямой две точки A и B. Сколько получилось лучей с началом в этих точках?
355. Сколько получится лучей, если на прямой отметить:
а) 3 точки; б) 5 точек; в) 100 точек?
Из одной точки выходят два луча.
а) 3 • 2 = 6 лучей;
б) 5 • 2 = 10 лучей;
в) 100 • 2 = 200 лучей.
356. Две прямые пересекаются в одной точке. Сколько лучей с началом в этой точке они образуют?
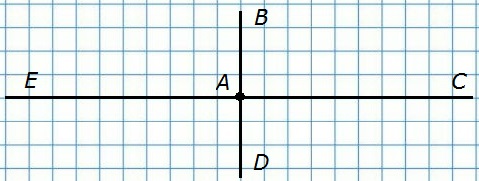
Лучи АС, АD, АЕ, АВ — всего 4 луча.
357. Назовите все лучи с вершиной в точках A, B и C (рис. 47). Сколько лучей получилось.
Лучи АM, АN, BM, ВN, CM, CN — всего 6 лучей.
358. Назовите все отрезки с концами в точках M, N и K (рис. 48). Сколько отрезков получилось?
Отрезки MА, MК, NК — всего 3 отрезка.
359. На прямой отметили четыре точки. Образовалось 6 отрезков с концами в этих точках. Проверьте.
Отрезки АВ, АС, АD, ВС, ВD, СD — всего 6 отрезков.
360. Перечертите рисунок 49 в тетрадь. Обозначьте все точки пересечения прямых, продолжив их, если нужно. На сколько частей разделилась плоскость? Выберите правильный ответ:
A. 10 частей;
Б. 11 частей;
В. 12 частей.
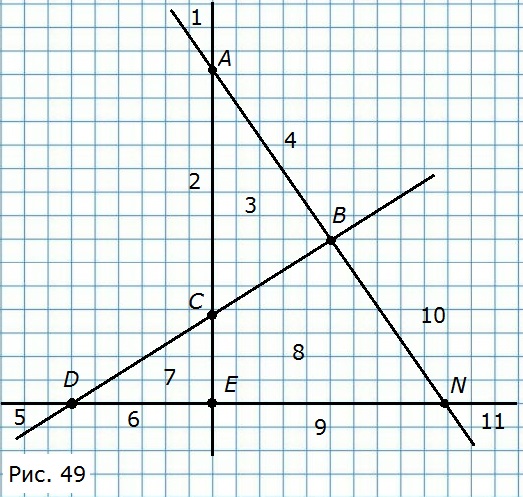
Ответ Б — 11 частей.