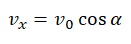На снимке полученном с помощью стробоскопа запечатлен прыжок со скалы предположим что
Движение тела, брошенного под углом к горизонту
теория по физике 🧲 кинематика
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты! График движения тела, брошенного под углом к горизонту:
α — угол, под которым было брошено тело
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
Уравнение координаты x:
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Алгоритм решения
Решение
Запишем исходные данные:
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Потенциальная энергия шарика в точке А равна:
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
Перед ударом кинетическая энергия шарика равна:
Согласно закону сохранения энергии:
E p A = E p B + E k B
Отсюда высота H равна:
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
pазбирался: Алиса Никитина | обсудить разбор | оценить
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Прогнозирование прыжка в длину и его проверка с учётом знаний физики
Бюджетное общеобразовательное учреждение «Русскополянская средняя общеобразовательная школа №2 имени Героя Советского Союза »
Школьное научное общество учащихся «Мысль»
Прогнозирование прыжка в длину и его проверка с учётом знаний физики
обучающиеся 9 «Б» класса
БОУ «Русскополянская школа №2».
Учитель физики БОУ «Русскополянская
Русская Поляна 2016
Учебный материал о движении тела, брошенного под углом к горизонту, является одним из наиболее сложных и, в то же время, важных в разделе «Механика» курса физики общеобразовательной школы. Задания, поэтому учебному материалу, предлагаются обучающимся основной средней школы на экзамене ОГЭ по физике в 9-м классе и обучающимся полной средней школы на экзамене ЕГЭ по физике в 11 классе. Однако учебного времени, отводимого различными имеющимися программами по физике на изучение данного учебного материала, явно недостаточно для всестороннего и глубокого его освоения. Мы думаем, что, значительную и действенную помощь в решении этой проблемы, может оказать предоставление возможности применить теоретические знания о движении тела, брошенного под углом к горизонту, на практике. В этом случае мы и наши одноклассники, пытаясь достичь практической цели, всесторонне и с неоднократными повторениями освоим непростой теоретический материал о движении тела, брошенного под углом к горизонту. Под «телом», брошенным под углом к горизонту, являемся мы сами, а выполняемые расчеты, кроме достижения практической цели, приводят к самопознанию, к уточнению и постижению своих спортивных возможностей. Как же это происходит, увидите далее. Мы считаем, что данная работа позволит нам улучшить результаты сдачи норм ГТО по прыжкам в длину.
Прежде чем выполнить это исследование мы провели опрос среди учащихся 9-х классов. В опросе приняли участие 55 респондентов.
2.Знаете ли вы, что для этого надо?
Цель: использование знаний законов движения тела, брошенного под углом к горизонту, для расчёта теоретически возможной дальности прыжка в длину у некоторых учащихся и проверка выполненного расчета на практике.
1.Изучить теоретический материал по данной теме.
2.Провести измерения и расчёты, необходимые для вычисления теоретической дальности прыжка.
3.Выполнить практическую часть.
4.Сравнить результаты и сделать вывод.
Материальная база: школьный стадион с использованием ямы для прыжков в длину, секундомер, рулетка измерительная, метровая линейка.
Гипотеза: Мы считаем, что знания физики помогают для достижения лучших спортивных результатов и хотим это проверить.
Объект исследования: учащиеся 9 «б» класса
Предмет исследования: знания законов физики по теме «движение тела, брошенного под углом к горизонту»
Метод обработки результатов;

Любое сложное движение материальной точки можно представить, как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить, как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1).
Проекции скорости тела, следовательно, изменяются со временем следующим образом:

где 
Координаты тела, следовательно, изменяются так:
При нашем выборе начала координат начальные координаты 
Проанализируем формулы (1). Определим время движения брошенного тела. Для этого положим координату y равной нулю, т. к. в момент приземления высота тела равна нулю. Отсюда получаем для времени полета:

Второе значение времени, при котором высота равна нулю, равно нулю, что соответствует моменту бросания, т. е. это значение также имеет физический смысл.
Дальность полета получим из первой формулы (1). Дальность полета – это значение координаты х в конце полета, т. е. в момент времени, равный t0. Подставляя значение (2) в первую формулу (1), получаем:

Из этой формулы видно, что наибольшая дальность полета достигается при значении угла бросания, равном 45 градусов.
Наибольшую высоту подъема брошенного тела можно получить из второй формулы (1). Для этого нужно подставить в эту формулу значение времени, равное половине времени полета (2), т. к. именно в средней точке траектории высота полета максимальна. Проводя вычисления, получаем

Из уравнений (1) можно получить уравнение траектории тела, т. е. уравнение, связывающее координаты х и у тела во время движения. Для этого нужно из первого уравнения (1) выразить время:
и подставить его во второе уравнение. Тогда получим:

Это уравнение является уравнением траектории движения. Видно, что это уравнение параболы, расположенной ветвями вниз, о чем говорит знак «-» перед квадратичным слагаемым. Следует иметь в виду, что угол бросания α и его функции – здесь просто константы, т. е. постоянные числа.
1.2 Теоретический материал.
Теория необходимая для расчётов.
Учащимся предлагается рассмотреть движение центра масс прыгуна (центр масс находится примерно на 10 см выше пупка) как движение материальной точки, брошенной под углом к горизонту с некоторой высоты h над поверхностью Земли и заканчивающей движение на высоте d ;
На снимке полученном с помощью стробоскопа запечатлен прыжок со скалы предположим что
На картинке приведена стробоскопическая фотография движения шарика по желобу. Промежутки времени между двумя последовательными вспышками света одинаковы. Числа на линейке обозначают длину в дециметрах. Как изменяются скорость шарика, его ускорение и сила тяжести, действующая на шарик? Начальную скорость шарика считать равной нулю.
К каждому элементу первого столбца подберите соответствующий элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами.
Б) Ускорение шарика
В) Сила тяжести, действующая на шарик
Сила тяжести, действующая на шарик, никак не зависит от скорости его движения. Она определяется только массой шарика и величиной ускорения свободного падения. Поскольку эти величины остаются постоянными при движении шарика вниз по желобу, сила тяжести не изменяется (В — 3). Из рисунка видно, что за равные промежутки времени шарик успевает проходить все большее расстояние, а значит, его скорость увеличивается (А — 1). Ускорение же шарика, остается постоянным (Б — 3). Действительно, при равноускоренном движении путь тела, начавшего движение из состояния покоя, изменяется со временем по квадратичному закону А из стробоскопической фотографии видно, что через равные промежутки времени координата шарика как раз изменяется по квадратичному закону:
На снимке полученном с помощью стробоскопа запечатлен прыжок со скалы предположим что
Тело бросили с горизонтальной площадки под углом 30° к горизонту с начальной скоростью 20 м/с. Затем бросок повторили, сообщив телу ту же по модулю начальную скорость, но увеличив угол её наклона к горизонту. Пренебрегая сопротивлением воздуха, определите, как при втором броске по сравнению с первым изменятся следующие физические величины: модуль импульса тела в высшей точке траектории; потенциальная энергия тела в высшей точке траектории.
Для каждой величины определите соответствующий характер изменения:
Запишите в ответ цифры, расположив их в порядке, соответствующем таблице:
| ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ | ИЗМЕНЕНИЕ ВЕЛИЧИНЫ |
| Модуль импульса тела в высшей точке траектории | Потенциальная энергия тела в высшей точке траектории |
Чем больше угол броска, тем большей высоты достигнет тело. Отсюда следует, что во втором случае потенциальная энергия тела в высшей точке траектории будет больше чем в первом случае.
В начале своего движения тело обладало только кинетической энергией, а в высшей точке траектории оно будет обладать как кинетической так и потенциальной энергией. Исходя из того, что начальная скорость тела в первом и втором случае одинакова, согласно закону сохранения энергии, увеличение потенциальной энергии в высшей точке траектории приведет к уменьшению кинетической энергии в высшей точке и, как следствие, к уменьшению импульса тела в высшей точке траектории.
Но ведь в высшей точке траектории скорость будет равна нулю в обоих случаях, а значит и импульс, в обоих случаях, равен нуля и меняться не будет.
В верхней точке траектории скорость равна нулю только при броске вертикально вверх. При броске под углом скорость в верхней точке траектории не равна нулю.
Камень бросили под углом к горизонту. Сопротивление воздуха пренебрежимо мало. В верхней точке траектории кинетическая энергия камня равна его потенциальной энергии (относительно поверхности Земли). Под каким углом к горизонту бросили камень? Ответ приведите в градусах.
Пусть скорость в начале броска равна а скорость в верхней точке траектории равна
В верхней точке траектории вертикальная составляющая скорости равна нулю, поэтому
По условию, в верхней точке траектории потенциальная энергия камня равна кинетической, используя этот факт, найдём
Воспользуемся законом сохранения энергии, энергия камня в начале броска равна энергии камня в верхней точке его траектории:
Косинус угла броска камня будет равен отношению к
Следовательно, угол броска равен 45°.
Камень бросили под углом к горизонту. Сопротивление воздуха пренебрежимо мало. В верхней точке траектории кинетическая энергия камня в 3 раза больше его потенциальной энергии (относительно поверхности Земли). Под каким углом к горизонту бросили камень? Ответ приведите в градусах.
Пусть скорость в начале броска равна а скорость в верхней точке траектории равна
В верхней точке траектории вертикальная составляющая скорости равна нулю, поэтому
По условию, в верхней точке траектории кинетическая энергия камня в три раза больше потенциальной, используя этот факт, найдём
Воспользуемся законом сохранения энергии, энергия камня в начале броска равна энергии камня в верхней точке его траектории:
Косинус угла броска камня будет равен отношению к
Следовательно, угол броска равен 30°.
Аналоги к заданию № 6129: 6164 Все
Тело бросили с горизонтальной площадки под углом 30° к горизонту с начальной скоростью 20 м/с. Затем бросок повторили, сообщив телу ту же по модулю начальную скорость, но увеличив угол её наклона к горизонту. Пренебрегая сопротивлением воздуха, определите, как при втором броске по сравнению с первым изменятся следующие физические величины: отношение максимальной высоты подъёма тела к дальности его полёта; кинетическая энергия тела в высшей точке траектории.
Для каждой величины определите соответствующий характер изменения:
Запишите в ответ цифры, расположив их в порядке, соответствующем таблице:
| Отношение максимальной высоты подъёма тела к дальности его полёта | Кинетическая энергия тела в высшей точке траектории |
Дальность полета и максимальная высота определяются формулами:
Их отношение равно:
Таким образом, увеличение угла броска приведет к увеличению отношения максимальной высоты подъёма тела к дальности его полёта
Чем больше угол броска, тем большей высоты достигнет тело. Отсюда следует, что во втором случае потенциальная энергия тела в высшей точке траектории будет больше чем в первом случае.В начале своего движения тело обладало только кинетической энергией, а в высшей точке траектории оно будет обладать как кинетической так и потенциальной энергией. Исходя из того, что начальная скорость тела в первом и втором случае одинакова, согласно закону сохранения энергии, увеличение потенциальной энергии в высшей точке траектории приведет к уменьшению кинетической энергии в высшей точке.
Аналоги к заданию № 9498: 9530 Все
Человек ростом h = 1,6 м, стоя на земле, кидает мяч из-за головы и хочет перебросить его через забор высотой H = 4,8 м, находящийся на расстоянии l = 6,4 м от него. Определите модуль скорости, с которой необходимо бросить мяч, чтобы он перелетел через забор, коснувшись его в верхней точке своей траектории? Сопротивлением воздуха пренебречь.
Известно, что в верхней точке траектории тела, брошенного под углом к горизонту, скорость направлена горизонтально. Без действия сопротивления воздуха тело движется с ускорением свободного падения. Поэтому по оси Ox движение является равномерным (горизонтальная проекция скорости одинакова на всем пути), по оси Oy движение равноускоренное, при этом в верхней точки траектории вертикальная проекция скорости равна 0.
Применим закон сохранения энергии для движения мячика от точки броска до верхней точки траектории
Учитывая, что найдем вертикальную проекцию начальной скорости:
Скорость тела при равноускоренном движении по вертикали равна откуда время подъема до верхней точки траектории
Зная расстояние, которое мяч пролетел по горизонтали, найдем горизонтальную составляющую начальной скорости
Тогда начальная скорость броска мяча
Человек ростом h, стоя на Земле, бросает из-за головы камень и хочет перебросить его через забор высотой H, находящийся на расстоянии L от человека. Найдите угол, под которым нужно бросить камень, чтобы он перелетел через забор, коснувшись его в верхней точке своей траектории.
Известно, что в верхней точке траектории тела, брошенного под углом к горизонту, скорость направлена горизонтально. Без действия сопротивления воздуха тело движется с ускорением свободного падения. Поэтому по оси Ox движение является равномерным (горизонтальная проекция скорости одинакова на всем пути), по оси Oy движение равноускоренное, при этом в верхней точки траектории вертикальная проекция скорости равна 0.
Применим закон сохранения энергии для движения мячика от точки броска до верхней точки траектории
Учитывая, что найдем вертикальную проекцию начальной скорости:
Скорость тела при равноускоренном движении по вертикали равна откуда время подъема до верхней точки траектории
Выразив из представленных формул горизонтальную и вертикальную составляющие начальной скорости, найдем тангенс угла броска:
откуда
Ответ:
Человек ростом h = 1,6 м, стоя на земле, кидает мяч из-за головы и хочет перебросить его через забор высотой H = 4,8 м, находящийся на расстоянии l = 6,4 м от него. Определите модуль скорости, с которой необходимо бросить мяч, чтобы он перелетел через забор, коснувшись его в верхней точке своей траектории? Сопротивлением воздуха пренебречь.
Какие законы Вы использовали для описания движения мяча? Обоснуйте их применение к данному случаю.
При отсутствии действия внешних сил (сила сопротивления воздуха равна нулю) система «мяч — Земля» является замкнутой. Поэтому в инерциальной системе отсчета применим закон сохранения энергии.
Перейдем к решению. Известно, что в верхней точке траектории тела, брошенного под углом к горизонту, скорость направлена горизонтально. Без действия сопротивления воздуха тело движется с ускорением свободного падения. Поэтому по оси Ox движение является равномерным (горизонтальная проекция скорости одинакова на всем пути), по оси Oy движение равноускоренное, при этом в верхней точки траектории вертикальная проекция скорости равна 0.
Применим закон сохранения энергии для движения мячика от точки броска до верхней точки траектории
Учитывая, что найдем вертикальную проекцию начальной скорости:
Скорость тела при равноускоренном движении по вертикали равна откуда время подъема до верхней точки траектории
Зная расстояние, которое мяч пролетел по горизонтали, найдем горизонтальную составляющую начальной скорости
Тогда начальная скорость броска мяча
Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиусом R со скоростью Как изменятся радиус траектории, период обращения и кинетическая энергия частицы при увеличении скорости её движения?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
обращенияКинетическая
На заряженную частицу со стороны магнитного поля действует сила Лоренца, которая сообщает ей центростремительное ускорение. Второй закон Ньютона приобретает вид: Отсюда следует, что при увеличении скорости движения частицы радиус траектории увеличивается. Период обращения связан со скоростью движения и радиусом траектории соотношением
В силу того, что
при увеличении скорости период обращения не изменяется. Кинетическая энергия равна
Следовательно, при увеличении скорости кинетическая энергия также увеличивается.
Эта строчка следствие второго закона Ньютона:
. А поскольку в данной задаче величина поля не изменяется, частица одна и та же, меняется только ее скорость, заключаем, что при увеличении скорости
не изменяется, а значит, не изменяется и
, что, в свою очередь, ведет к неизменности периода.
Частица массой m, несущая заряд q, движется в однородном магнитном поле с индукцией В по окружности радиусом R со скоростью Как изменится радиус траектории, период обращения и кинетическая энергия частицы при уменьшении скорости ее движения?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
обращенияКинетическая
На заряженную частицу со стороны магнитного поля действует сила Лоренца, которая сообщает ей центростремительное ускорение. Второй закон Ньютона приобретает вид: Отсюда следует, что при уменьшении скорости движения частицы радиус траектории уменьшается. Период обращения связан со скоростью движения и радиусом траектории соотношением
В силу того, что
при уменьшении скорости период обращения не изменяется. Кинетическая энергия равна
Следовательно, при уменьшении скорости кинетическая энергия также уменьшается.
Положительный заряд перемещается в однородном электростатическом поле из точки 1 в точку 2 по разным траекториям. При перемещении по какой траектории электрическое поле совершает наименьшую работу?
4) работа одинакова при движении по всем траекториям
Электростатическое поле потенциально. Это значит, что работа электрического поля не зависит от формы траектории и определяется только начальным и конечным положениями заряда.
Точечное тело бросают с поверхности земли под углом α к горизонту с начальной скоростью V0. Как изменятся при увеличении угла бросания тела
А) отношение максимальной высоты подъёма к дальности полёта и
Б) отношение модуля импульса в верхней точке траектории к модулю импульса при броске?
Для каждой величины определите соответствующий характер изменения:
Запишите в ответ цифры, расположив их в порядке, соответствующем таблице:
Отношение максимальной высоты подъёма к дальности полёта
Отношение модуля импульса в верхней точке траектории к модулю импульса при броске
Максимальная высота подъёма равна дальность полёта равна
Их отношение
увеличится при увеличении угла бросания тела.
В наивысшей точке траектории вертикальная составляющая скорости тела равна нулю, следовательно, модуль скорости тела равен модулю проекции скорости тела на горизонтальную ось: При увеличении угла броска косинус
уменьшится, следовательно, уменьшится и
Поскольку модуль начальной скорости остался прежним, отношение модуля импульса в верхней точке траектории к модулю импульса при броске уменьшится.
Сравниваются импульсы тел в верхней точке траектории, в которой проекция на ось у равна 0. Ошибки нет.
Ученик исследовал движение шарика, сброшенного горизонтально со стола. Для этого он измерил координаты летящего шарика в разные моменты времени его движения и заполнил таблицу:
| t, c | 0 | 0,05 | 0,1 | 0,15 | 0,2 |
| x, см | 0 | 5,5 | 13,5 | 17,5 | 24 |
| y, см | 0 | 1,5 | 4,5 | 11,5 | 20 |
Погрешность измерения координат равна 1 см, а промежутков времени — 0,01 с. На каком из графиков верно представлена наиболее вероятная траектория движения шарика?
В задании нужно найти график, на котором наиболее верно представлена траектория движения шарика, поэтому графики 3 и 4 сразу отпадают, так как на них отображена не возможная траектория, а зависимость координат от времени. Остается выбрать между графиками 1 и 2. Как известно, свободно падающее тело летит по параболе. Следовательно, через экспериментальные точки нужно проводить параболическую интерполяционную кривую, что и сделано на рисунке 1.
Ученик исследовал движение шарика, сброшенного горизонтально со стола. Для этого он измерил координаты летящего шарика в разные моменты времени его движения и заполнил таблицу:
Погрешность измерения координат равна 1 см, а промежутков времени — 0,01 с. На каком из графиков верно представлена наиболее вероятная траектория движения шарика?
В задании нужно найти график, на котором наиболее верно представлена траектория движения шарика, поэтому графики 3 и 4 сразу отпадают, так как на них отображена не возможная траектория, а зависимость координат от времени. Остается выбрать между графиками 1 и 2. Известно, что свободно падающее тело летит по параболе. Следовательно, через экспериментальные точки нужно проводить параболическую интерполяционную кривую, что и сделано на рисунке 2.
В установке, изображённой на рисунке, грузик А соединён перекинутой через блок нитью с бруском В, лежащим на горизонтальной поверхности трибометра, закреплённого на столе. Грузик отводят в сторону, приподнимая его на некоторую высоту h, и отпускают. Какую величину должна превзойти эта высота, чтобы брусок сдвинулся с места в тот момент, когда грузик проходит нижнюю точку траектории? Масса грузика m, масса бруска М, длина свисающей части нити L, коэффициент трения между бруском и поверхностью Трением в блоке, а также размерами блока пренебречь.
1. На брусок B, пока он не пришёл в движение, действует сила тяжести сила реакции опоры
сила натяжения нити
и сила трения покоя
максимальное значение которой
Для того, чтобы он пришёл в движение, должно выполняться условие
На грузик А в нижней точке траектории действует сила тяжести сила натяжения нити
модуль которой равен модулю силы
и равен
При этом грузик в этой точке движется со скоростью
и на него действует центростремительное ускорение
направленное по радиусу к центру окружности и равное
2. Запишем второй закон Ньютона для каждого тела в проекциях:
3. По закону сохранения энергии потенциальная энергия грузика, поднятого на высоту равна кинетической энергии грузика в нижней точке траектории:
4. С учётом условия движения бруска получаем
Ответ:
В установке, изображённой на рисунке, грузик А соединён перекинутой через блок нитью с бруском В, лежащим на горизонтальной поверхности трибометра, закреплённого на столе. Грузик отводят в сторону, приподнимая его на высоту h, и отпускают. Длина свисающей части нити равна L. Какую величину должна превзойти масса грузика, чтобы брусок сдвинулся с места в момент прохождения грузиком нижней точки траектории? Масса бруска М, коэффициент трения между бруском и поверхностью Трением в блоке, а также размерами блока пренебречь.
1. На брусок B, пока он не пришёл в движение, действуют сила тяжести сила реакции опоры
сила натяжения нити
и сила трения покоя
максимальное значение которой
Для того чтобы он пришёл в движение, должно выполняться условие
На грузик А в нижней точке траектории действуют сила тяжести и сила натяжения нити
модуль которой равен модулю силы
и равен
При этом грузик в этой точке движется со скоростью
то есть он движется с центростремительным ускорением
направленным по радиусу к центру окружности и равным
2. Запишем второй закон Ньютона для каждого тела в проекциях:
3. По закону сохранения энергии потенциальная энергия грузика, поднятого на высоту равна кинетической энергии грузика в нижней точке траектории:
4. С учётом условия движения бруска получаем
Ответ: