Найдите сопротивление rab считая что все звенья проволочной звезды
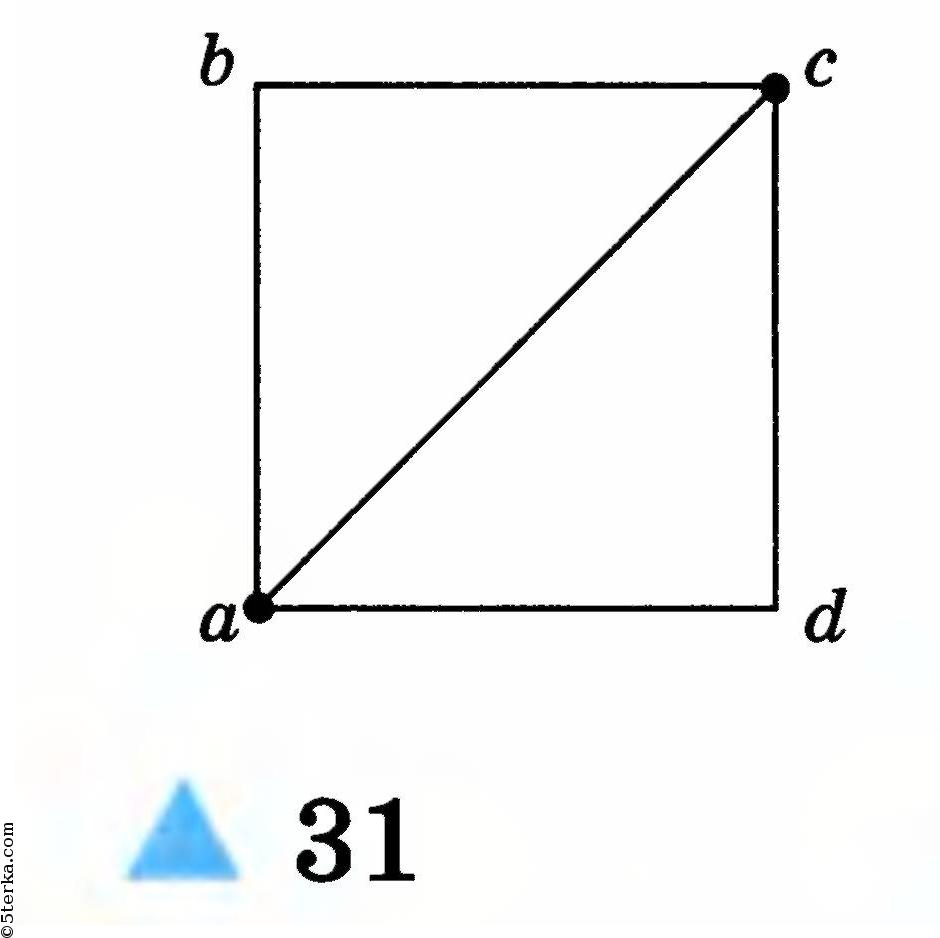
2. Сопротивление стороны проволочного квадрата (рис. 31) равно R. Найдите сопротивления Rac,Rad,Rcd.
Сопротивление между точками а и с по теореме Пифагора равно
Общее сопротивление Rac легко сосчитать, заменив сперва последовательно соединенные резисторы сопротивлениями 2R, а потом параллельно соединенные оставшиеся резисторы.
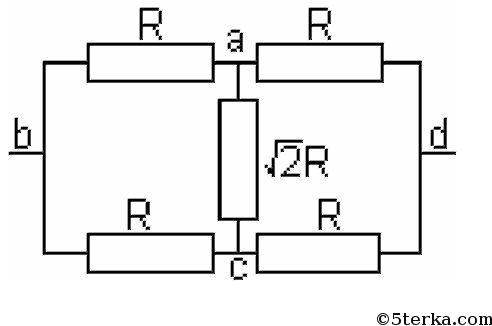
Преобразуем схему квадрата так, как показано на рисунке 1. Дальше полученную схему легко
соединены параллельно, заменим их на
R1 соединено последовательно с R, их можно заменить на
Тогда эквивалентное сопротивление
Если рассматривать схему на рисунке 2, то через сопротивление ас ток идти не будет, а следовательно его сопротивление равно нулю (схема симметрична, то есть произведения сопротивлений противоположных плечей равны). Значит сопротивление
можно выкинуть из цепи.
Дальше заменим последовательно соединенные резисторы на их эквиваленты 2R, которые соединены параллельно. Таким образом Эквивалентное сопротивление цепи Rbd = R.
Электродинамика (стр. 4 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
Рассчитаем сопротивление схемы, содержащей точки с одинаковым потенциалом.
Пусть резисторы Rl, R2, R3, R4, R5 соединены по схеме, изображенной на рисунке 29, а, называемой мостиком Уитстона. Выясним, при каком соотношении сопротивлений ток через резистор R5 не протекает, а также найдем сопротивление между точками а и & в этом случае.
Предположим, что ток через резистор R5 не протекает, тогда через резистор R3 протекает такой же ток It, как и через резистор R1. Соответственно, ток 12 будет протекать как через резистор R2, так и через R4. Отсутствие тока между точками cvid означает, что их потенциалы равны
Фс = Фа-Следовательно, будут равны друг другу и разности потенциалов
С учетом закона Ома для однородного участка цепи из формулы (24) следует, что
Разделим почленно первое равенство в системе (25) на второе:
Постоянный электрический ток
Ток через резистор R5 не протекает, если произведения сопротивлений противоположных плечей мостика равны друг другу.
Мостиковую схему используют для измерения одного из неизвестных сопротивлений, входящих в плечи мостика, например R1. Оно находится из формулы (26). Найдем сопротивление между точками а и Ь, когда jRj = R3 = R и R2 = R4 = SR, т. е. условие (26) выполняется.
Равенство потенциалов точек с и d позволяет использовать любую из эквивалентных схем, представленных на рисунке 29, б. В первой схеме резистор R5 не используется: цепь между точками cud разомкнута. Во второй схеме точки cud соединены перемычкой.
В первой схеме резисторы R и SR соединены последовательно. Это приводит к параллельному соединению двух резисторов, сопротивления которых по 4R, и результирующему сопротивлению 2R между точками а иЪ.
Во второй схеме резисторы, сопротивление которых R, соединены
между собой соединены и два резистора 3R. Первая
пара резисторов, сопротивление которых R/2, соединена со второй, имеющей сопротивление 3JR/2, последовательно. Естественно, что результирующее сопротивление между точками а и Ъ оказывается равным 2R, как и при использовании первой схемы. Результат расчета не должен зависеть от способа его получения.
1. Какова последовательность расчета сопротивления смешанного соединения проводников?
2. В чем характерная особенность электрических схем с перемычками?
3. Почему наличие точек с равным потенциалом облегчает расчет электрических схем?
4. При каком условии возникает баланс плеч в мостике Уитстона?
5. Чему равно сопротивление мостика Уитстона между точками а и Ь?
1 ■ Найдите сопротивление схемы, изображенной на рисунке 30. [5Д/11 ]
2. Сопротивление стороны проволочного квадрата (рис. 31) равно R. Найдите сопро
тивления Дос, Rad, Rcd.
3. Найдите сопротивление Rab, считая, что все звенья проволочной звезды имеют со
противление R (рис. 32). [7Д/6]
4- Сопротивление любого ребра проволочного каркаса куба равно R, Найдите сопротивление между наиболее удаленными друг от друга вершинами куба (рис. 33).
Физический портал для школьников и абитуриентов
Вы здесь
Подготовка к олимпиаде. Методы расчета резисторных схем постоянного тока. 1.4. Расчет эквивалентных сопротивлений бесконечных цепей


Методы расчета резисторных схем постоянного тока
1.4. Расчет эквивалентных сопротивлений бесконечных цепей
Особую группу образуют задачи на расчет эквивалентных сопротивлений бесконечных цепей. Как правило, эти цепи симметричны и во многих случаях содержат одинаковые элементы (резисторы). Рассматриваемые задачи можно разбить на три группы: а> линейные (одномерные); б) плоскостные (двумерные); в) объемные (трехмерные). Эвристические приемы решения подобных задач просты и достаточно оригинальны. Причем последние два типа задач решаются только с помощью искусственного приема, содержание которого будет рассмотрено ниже.
1.4.1. Расчет эквивалентных сопротивлений линейных бесконечных цепей
Найдем эквивалентное сопротивление типичной линейной бесконечной цепи резисторов, состоящей из повторяющихся элементов (секций), в типичной задаче.
Задача 15. Найдите эквивалентное сопротивление бесконечной цепочки (рис.), которая состоит из одинаковых резисторов сопротивлением R каждый.
Решение (типовое, алгоритм). Для нахождения эквивалентного сопротивления цепи необходимо выделить общую секцию, которая бесконечно повторяется. Вполне очевидно, что если отделить ее от цепи, то общее сопротивление этой цепи не изменится, т.к. число элементов (секций) бесконечно. В силу вышесказанного, выделив повторяющуюся секцию в цепи и заменив сопротивление, остальной цепи искомым сопротивлением Rх, получим эквивалентную схему (рис.).
Найдем сопротивление цепи, предварительно записав выражение для Rх через Rx. Опуская промежуточные выкладки, получим:
откуда получим ответ:
Рассмотрим еще одну подобную задачу.
Задача 16. Найдите эквивалентное сопротивление бесконечной цепочки (рис.), которая состоит из одинаковых резисторов сопротивлением R каждый.
Решение. Применим точно такой же прием, но с другой повторяющейся секцией (рис.).
После аналогичных расчетов получим:
Отсюда легко записать ответ:
Можно сформулировать более сложные задачи, решение которых сводится к рассмотренным выше алгоритмам.
Задача 17. Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки (рис.), которая состоит из одинаковых резисторов сопротивлением R каждый.
Решение. Эквивалентное сопротивление цепи равно сопротивлению двух одинаковых и параллельно соединенных резисторов, сопротивления которых равны (см. решения задач 15 и 16): справа
Тогда после простых расчетов легко получить ответ:
Задача 18. Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки (рис.), которая состоит из одинаковых резисторов сопротивлением R каждый.
Решение. Эквивалентное сопротивление цепи равно сопротивлению двух одинаковых и параллельно соединенных резисторов сопротивлением
каждый (см. решение задачи 16). Отсюда легко получить ответ:
Задача 19. Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки (рис.), которая состоит из одинаковых резисторов сопротивлением R каждый.
Решение. Эквивалентное сопротивление цепи равно сопротивлению четырех резисторов, соединенных между собой в цепь, которая изображена на рис.
(см. решения задач 15 и 16). Отсюда искомое эквивалентное сопротивление цепи между точками А и В:
Задача 20. Найдите эквивалентное сопротивление между точками А и В бесконечной цепочки (рис.), которая состоит из одинаковых проволочных резисторов сопротивлением R каждый.
Решение. Эквивалентная схема представлена на рис.
Повторяющаяся секция состоит из четырех резисторов. Полное сопротивление цепи находим, полагая RAB = Rх. Опуская промежуточные выкладки, получим
откуда следует, что
Второй корень уравнения отрицательный и не имеет смысла. Окончательный результат:
Рассмотрим более трудную задачу, решение которой предполагает предварительное использование метода исключения пассивных элементов цепи.
Задача 21. Найти эквивалентное сопротивление между точками А и В бесконечной цепочки (рис. а), которая состоит из одинаковых проволочных резисторов сопротивлением R каждый.
Решение. Чтобы найти эквивалентное сопротивление цепи, необходимо сначала выделить общую секцию, которая бесконечно повторяется. Понятно, что если отделить ее от цепи, то общее сопротивление этой цепи не изменится. Выделить повторяющуюся секцию в рассматриваемой цепи можно, но заменить сопротивление остальной части цепи искомым сопротивлением Rх нельзя, т.к. оставшаяся часть имеет четыре соединительных провода. Если посмотрим на каркас слева, то получим изображение цепи в перспективе, приведенное на рисунке б.
Из симметрии этого рисунка видно, что потенциалы точек, обозначенных цифрой 1, одинаковы и равны потенциалам точек, обозначенных цифрой 2. Исключим из рассмотрения пассивные резисторы, соединяющие точки 1 и 2 (рис. в).
Между точками С и D (рис. в) находится фигура, эквивалентное сопротивление которой равно искомому, т.к. цепь бесконечна. Обозначим искомое сопротивление через Rх (рис. г)
и получим (аналогично решению задачи 15)
откуда следует, что
Второй корень уравнения отрицательный и не имеет смысла. Окончательный результат:
При решении задач с плоскостными и объемными цепями используется несколько другой подход.
Найдите сопротивление rab считая что все звенья проволочной звезды


Решебник по Физике. 11 класс. Касьянов. Все уровени





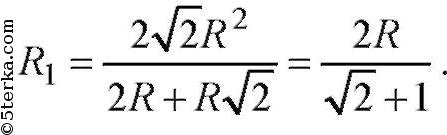


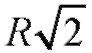








































 Скачать бесплатно Решебник и ГДЗ по Физике. 10 класс. В.А. Касьянов
Скачать бесплатно Решебник и ГДЗ по Физике. 10 класс. В.А. Касьянов