Назовите основные виды измерений чем они характеризуются

Классификация видов измерений

Измерения различают по способу получения информации, по характеру изменений измеряемой величины в процессе измерений, по количеству измерительной информации, по отношению к основным единицам.

По способу получения информации измерения разделяют на прямые, косвенные, совокупные и совместные.

Прямые измерения – это непосредственное сравнение физической величины с ее мерой. Например, при определении длины предмета линейкой происходит сравнение искомой величины (количественного выражения значения длины) с мерой, т. е. линейкой.

Косвенные измерения – отличаются от прямых тем, что искомое значение величины устанавливают по результатам прямых измерений таких величин, которые связаны с искомой определенной зависимостью. Так, если измерить силу тока амперметром, а напряжение вольтметром, то по известной функциональной взаимосвязи всех трех величин можно рассчитать мощность электрической цепи.

Совокупные измерения – сопряжены с решением системы уравнений, составляемых по результатам одновременных измерений нескольких однородных величин. Решение системы уравнений дает возможность вычислить искомую величину.

Совместные измерения – это измерения двух или более неоднородных физических величин для определения зависимости между ними.

Совокупные и совместные измерения часто применяют в измерениях различных параметров и характеристик в области электротехники.

По характеру изменения измеряемой величины в процессе измерений бывают статистические, динамические и статические измерения.

Статистические измерения связаны с определением характеристик случайных процессов, звуковых сигналов, уровня шумов и т. д. Статические измерения имеют место тогда, когда измеряемая величина практически постоянна.

Динамические измерения связаны с такими величинами, которые в процессе измерений претерпевают те или иные изменения. Статические и динамические измерения в идеальном виде на практике редки.

По количеству измерительной информации различают однократные и многократные измерения.

Однократные измерения – это одно измерение одной величины, т. е. число измерений равно числу измеряемых величин. Практическое применение такого вида измерений всегда сопряжено с большими погрешностями, поэтому следует проводить не менее трех однократных измерений и находить конечный результат как среднее арифметическое значение.

Многократные измерения характеризуются превышением числа измерений количества измеряемых величин. Преимущество многократных измерений – в значительном снижении влияний случайных факторов на погрешность измерения.

По условиям, определяющим точность результата, измерения делятся на три класса: измерения максимально возможной точности, достижимой при существующем уровнетехники; контрольно-поверочные измерения, погрешность которых не должна превышать некоторое заданное значение; технические (рабочие) измерения, в которых погрешность результата измерения определяется характеристиками средств измерений.

Источник

Виды измерений

Существует несколько видов измерений. При их классификации обычно исходят из характера зависимости измеряемой величины от времени, вида уравнения измерений, условий, определяющих точность результата измерений и способов выражения этих результатов.

1) По характеру зависимости измеряемой величины от времени:

б) динамические, связанные с величинами, которые в процессе измерений претерпевают те или иные изменения (измерения пульсирующих давлений, вибраций).

2) По способу получения результатов:

а) Прямые измерения — измерения, при которых искомое значение физической величины находят непосредственно из опытных данных путем ее непосредственного сравнения с мерой. (измерение давления, температуры и др.).

б) Косвенные измерения — измерения, при которых искомую величину определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, т.е. измеряют не собственно определяемую величину, а другие, функционально с ней связанные. Значение измеряемой величины находят через преобразование или через установленную формулу ( определение объема тела по прямым измерениям его геометрических размеров, нахождение удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения).

в) Совокупные измерения — это производимые одновременно измерения нескольких одноименных величин, характеризующих Данный предмет или изделие, при которых искомую определяют решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин ( определение массы отдельных гирь набора (или прогнозирование погоды на основе замеров силы ветра, влажности воздуха, фронтов и т.п).

г) Совместные измерения — это производимые одновременно измерения двух или нескольких неоднородных физических величин для нахождения зависимостей между ними (измерение электрического сопротивления при определенных температурных параметрах и температурных коэффициентов измерительного резистора по данным прямых измерений его сопротивления при различных температурах).

3) По условиям, определяющим точность результата:

а) Измерения максимально возможнойточности, достижимой при существующем уровне техники.

К ним относятся в первую очередь эталонные измерения, связанные с максимально возможной точностью воспроизведения установленных единиц физических величин, и, кроме того, измерения физических констант, прежде всего универсальных (например, абсолютного значения ускорения свободного падения и др.). К этому же классу относятся и некоторые специальные измерения, требующие высокой точности.

б) Контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторого заданного значения.

К ним относятся измерения, выполняемые лабораториями государственного надзора за внедрением и соблюдением стандартов и состоянием измерительной техники и заводскими измерительными лабораториями, которые гарантируют погрешность результата с определенной вероятностью, не превышающей некоторого заранее заданного значения.

в) Технические измерения, в которых погрешность результата определяется характеристиками средств измерений.

Примерами технических измерений являются измерения, выполняемые в процессе производства на машиностроительных предприятиях, на щитах распределительных устройств электрических станций и др.

4) По способу выражения результатов измерений:

а) Абсолютными называются измерения, которые основаны на прямых измерениях одной или нескольких основных величин или на использовании значений физических констант (определение длины в метрах, силы электрического тока в амперах, ускорения свободного падения в метрах на секунду в квадрате).

б) Относительными называются измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную (измерение относительной влажности воздуха, определяемой как отношение количества водяных паров в 1 м» 3 воздуха к количеству водяных паров, которое насыщает 1 m j воздуха при данной температуре).

5) По характеру изменения измеряемой величины измерения:

а) Статические — применяют для измерения случайных процессов, а затем для определения среднестатистической величины;

б) Постоянные — используют для контроля непрерывных процессов.

6) По количеству измерительной информации измерения:

а) Однократные измерения — это одно измерение одной величины, т.е. число измерений равно числу измеряемых величин. Практическое применение такого вида измерений всегда сопряжено с большими погрешностями.

б) Многократные измерения — характеризуются превышением числа измерений количества измеряемых величин. Преимущество многократных измерений — значительное снижение влияний случайных факторов на погрешность измерения.

Основными характеристиками измерений являются:

Принцип измерении — физическое явление или совокупность физических явлений, положенных в основу измерений (измерение массы тела при помощи взвешивания с использованием силы тяжести, пропорциональной массе, измерение температуры с использованием термоэлектрического эффекта).

Метод измерений — совокупность приемов использования принципов и средств измерений. Средствами измерений являются используемые технические средства, имеющие нормированные метрологические свойства.

При измерении методом непосредственной оценки искомое значение величины определяют непосредственно по отсчетному устройству средства измерения, которое проградуировано в соответствующих единицах.

Метод сравнения с мерой — метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой (например, сравнение массы на рычажных весах). Отличительной чертой методов сравнения является непо­средственное участие меры в процедуре измерения, в то время как в методе непосредственной оценки мера в явном виде при измерении не присутствует, а ее размеры перенесены на отсчетное устройство (шкалу) средства измерения заранее, при его градуировке. Обязательным в методе сравнения является наличие сравнивающего устройства.

Метод сравнения с мерой имеет несколько разновидностей: нулевой метод, дифференциальный метод, метод замещения и метод совпадений.

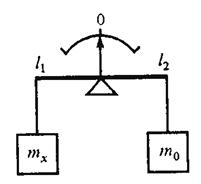
Нулевой метод (или метод полного уравновешивания) — метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и встречного воздействия меры на сравнивающее устройство сводят к нулю.

Например. Измерение массы на равноплечих весах, когда воздействие на весы массы m_х полностью уравновешивается массой гирь m₀ (рисунок 2).

Рисунок 2 – Метод полного уравновешивания

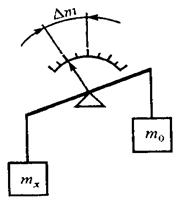
При дифференциальном методе полное уравновешивание не производят, а разность между измеряемой величиной и величиной, воспроизводимой мерой, отсчитывается по шкале прибора.

Например. Измерение массы на равноплечих весах, когда воздействие массы m_х на весы частично уравновешивается массой гирь m₀, а разность масс отсчитывается по шкале весов, градуированной в единицах массы (рисунок 3).

Рисунок 3 – Дифференциальный метод

В этом случае значение измеряемой величины m_х = m₀ + m, где m — показания весов

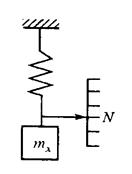
Метод замещения — метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой.

Например.Взвешивание на пружинных весах. Измерение производят в два приема. Вначале на чашу весов помещают взвешиваемую массу и отмечают положение указателя весов; затем массу m_х замещают массой гирь m₀, подбирая ее так, чтобы указатель весов установился точно в том же положении, что и в первом случае. При этом ясно, что m_х = m₀, (рисунок 4).

Рисунок 4 – Метод замещения

В методе совпадений разность между измеряемой величиной и величиной воспроизводимой мерой измеряют, используя совпадения отметок шкал или периодических сигналов.

Например. Измерение числа оборотов вала с помощью стробоскопа — вал периодически освещается вспышками света, и частоту вспышек подбирают так, чтобы метка, нанесенная на вал, казалась наблюдателю неподвижной. Метод совпадений, использующий совпадения основной и нониусной отметок шкал, реализуется в штангенприборах, применяемых для измерения линейных размеров.

Погрешность измерений — отклонение результата измерений от истинного значения измеряемой величины. Погрешность вызывается воздействием множества факторов, таких как: характер измеряемой величины, качество применяемых средств измерений, метод измерений, условия измерения (температура, влажность, давление и т.п.), индивидуальные особенности лица, выполняющего измерения, и др. Под влиянием этих факторов результат измерений будет отличаться от истинного значения измеряемой величины.

Точность измерений — качественная характеристика измерений, отражающая близость их результатов к истинному значению измеряемой величины.

Количественно точность можно выразить величиной «класс точности». Это характеристика, зависящая от способа выражения пределов допускаемых погрешностей средств измерений. Введение класса точности преследовало цель классификации средств измерений по точности. В настоящее время, когда схемы и конструкции средств измерений усложнились, а области применения средств измерений весьма расширились, на погрешность измерений стали существенно влиять и другие факторы: изменения внешних условий и характер изменения измеряемых величин во времени.

Погрешность измерительных приборов перестала быть основной составляющей погрешности измерений, и класс точности не позволяет в полной мере решать практические задачи, перечисленные выше. Область практического применения характеристики «класс точности» ограничена только такими средствами измерений, которые предназначены для измерения статических величин. В международной практике «класс точности» устанавливается только для небольшой части приборов.

Правильность измерений — качество измерений, отражающее близость к нулю систематических погрешностей в их результатах (т.е. таких погрешностей, которые остаются постоянными или закономерно изменяются при повторных измерениях одной и той же величины). Правильность измерений зависит, в частности, от того, насколько действительный размер единицы, в которой выполнено измерение, отличается от ее истинного размера (по определению), т.е. от того, в какой степени были правильны (верны) средства измерений, использованные для данного вида измерений.

Достоверность характеризует доверие к результатам измерений и делит их на две категории: достоверные и недостоверные, в зависимости от того, известны или неизвестны вероятностные характеристики их отклонений от истинных значений соответствующих величин. Поэтому такие вероятности следует рассматривать в качестве критериев достоверности контроля, чтобы в границах допуска правильно охарактеризовать параметры качества и безопасности.

Наличие погрешности ограничивает достоверность измерений, т.е. вносит ограничение в число достоверных значащих цифр числового значения измеряемой величины и определяет точность измерений. Характеристики погрешности измерений должны выбираться при контроле образцов продукции в соответствии с требованиями достоверности контроля.

Измерения как основной объект метрологии связаны в основном с физическими величинами:

Физическая величина — одно из свойств физического объекта, явления, процесса, который является общим в качественном отношении для многих физических объектов, отличаясь при этом количественным значением.

Физическая величина, которой по определению присвоено числовое значение, равное единице, называется единицей физической величины.

Различают основные и производные единицы.

Основные единицы физической величины выбираются произвольно, независимо от других единиц ( единица длины — метр, единица массы — килограмм, единица температуры — градус и т.д.)

Единицы, образованные с помощью формул, выражающих зависимость между физическими величинами, называют производными единицами. В этом случае единицы величин будут выражаться через единицы других величин. Например, единица скорости — метр в секунду (м/с), единица плотности — килограмм на метр в квадрате (кг/м 2 ).

Единицы физических величин объединяются по определенному принципу в системы единиц. Эти принципы заключаются в следующем: произвольно устанавливают единицы для некоторых величин, называемых основными единицами, и по формулам через основные получают все производные единицы для данной области измерений. Совокупность основных и производных единиц, относящихся к некоторой системе величин и образованная в соответствии с принятыми принципами, составляет систему единиц физических величии.

Многообразие систем единиц для различных областей измерений создавало трудности в научной и экономической деятельности как в отдельных странах, так и в международном масштабе. Поэтому возникла необходимость в создании единой системы единиц, которая включала бы в себя единицы величин для всех разделов физики.

Международная система единиц состоит из семи основных единиц, двух дополнительных единиц и необходимого числа производных единиц.

К основным относятся:

— единица длины — метр — длина пути, которую проходитсвет в вакууме за 1/299792458 долю секунды;

— единица массы — килограмм — масса, равная массе международного прототипа килограмма;

— единица времени — секунда — продолжительность9192631770 периодов излучения, соответствующего переходу между двумя уровнями сверхтонкой структуры основного состояния атома цезия-133 при отсутствии возмущения со стороны внешних полей;

— единица силы электрического тока — ампер — сила неизменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого ввакууме, создал бы между этими проводниками силу, равную 2 • 10

7 Н на каждый метр длины;

— единица термодинамической температуры — кельвин — часть термодинамической температуры тройной точки воды. Допускается также применение шкалы Цельсия;

— единица количества вещества — моль — количество вещества системы, содержащей столько же структурных элементов, сколько атомов содержится в нуклиде углерода-12 массой 0,012 кг;

— единица силы света — кандела — сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540- 10 12 Гц, энергетическая сила которого в этом направлении составляет 1/683 Вт/ср».

Три первые единицы (метр, килограмм, секунда) позволяют образовать производные единицы для измерения механических и акустических величин. При добавлении к указанным четвертой единицы — кельвина можно образовать производные единицы для измерений тепловых величин.

Единицы (метр, килограмм, секунда, ампер) служат основой для образования производных единиц в области электрических, магнитных измерений и измерений ионизирующих излучений. Единица моль используется для образования единиц в области физико-химических измерений.

Дополнительными единицами являются:

Единица плоского угла — радиан и единица телесного угла — стерадиан используются для образования производных единиц, связанных с угловыми величинами (например, угловая скорость, световой поток и др.).

ШКАЛЫ ИЗМЕРЕНИЙ

Шкала наименований – это качественная, а не количественная шкала, она не содержит нуля и единиц измерений (напр., шкала цветов).

Такие шкалы используется для классификации объектов, свойства которых проявляются только в отношении эквивалентности (совпадения или несовпадения). Эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида не являются шкалами ФВ. В шкалах наименований оценивание осуществляется с использованием органов чувств человека, наиболее адекватен результат, выбранный большинством экспертов. Поскольку данные шкалы характеризуются только отношениями эквивалентности, то в них отсутствуют понятия нуля, «больше или меньше» и единицы измерения.

Шкала порядка – характеризует значение измеряемой величины в баллах (напр., шкала землетрясений; силы ветра и др.).

Шкала интервалов – имеет условное нулевое значение, а интервалы устанавливают по согласованию (напр., шкала времени, шкала длины).

Данные шкалы являются дальнейшим развитием шкал порядка. Шкала состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. К таким шкалам относится летоисчисление, температурные шкалы.

Шкала отношений – имеет естественное нулевое значение, а единица измерений устанавливается по согласованию, в зависимости от требования точности измерения (напр., шкала веса).

С формальной точки зрения эта шкала является шкалой интервалов с естественным началом отсчета. К значениям, полученным по шкале отношений, применимы все арифметические действия, что имеет большое значение при измерении ФВ.

Источник

Лекция 2. Виды и методы измерений

Описание

1. Основные понятия и определения. Виды измерений.

2. Методы измерений.

3. Понятие о точности измерений.

4. Основы обеспечения единства измерений

Оглавление

1. Основные понятия и определения. Виды измерений

Измерение — совокупность операций по применению системы измерений для получения значения измеряемой физической величины.

Измерения могут быть классифицированы по метрологическому назначению на три категории:

Ненормированные – измерения при ненормированных метрологических характеристиках.

Технические – измерения при помощи рабочих средств измерений.

Метрологические – измерения при помощи эталонов и образцовых средств измерений.

Ненормированные измерения наиболее простые. В них не нормируются точность и достоверность результата. Поэтому область их применения ограничена. Они не могут быть применены в области, на которую распространяется требование единства измерений. Каждый из нас выполнял ненормированные измерения длины, массы, времени, температуры не задумываясь о точности и достоверности результата. Как правило, результаты ненормированных измерений применяются индивидуально, т.е. используются субъектом в собственных целях.

Технические измерения удовлетворяют требованиям единства измерений, т.е. результат бывает получен с известной погрешностью и вероятностью, записывается в установленных единицах физических величин, с определённым количеством значащих цифр. Выполняются при помощи средств измерений с назначенным классом точности, прошедших поверку или калибровку в метрологической службе. В зависимости от того, предназначены измерения для внутрипроизводственных целей или их результаты будут доступны для всеобщего применения, необходимо выполнение калибровки или поверки средств измерений. Средство измерений, прошедшее калибровку или поверку, называют рабочим средством измерений. Примером технических измерений является большинство производственных измерений, измерение квартирными счётчиками потреблённой электроэнергии, измерения при взвешивании в торговых центрах, финансовые измерения в банковских терминалах. Средство измерений, применяемое для калибровки других средств измерений, называют образцовым средством измерений. Образцовое средство измерений имеет повышенный класс точности и хранится отдельно, для технических измерений не применяется.

Метрологические измерения не просто удовлетворяют требованиям единства измерений, а являются одним из средств обеспечения единства измерений. Выполняются с целью воспроизведения единиц физических величин для передачи их размера образцовым и рабочим средствам измерений. Метрологические измерения выполняет метрологическая служба в стандартных условиях, сертифицированным персоналом.

В дисциплине «Метрология, стандартизация и сертификация» рассматриваются технические измерения.

Можно выделить следующие виды измерений.

1) По характеру зависимости измеряемой величины от времени методы измерений подразделяются на:

2) По способу получения результатов измерений (виду уравнений измерений) методы измерений разделяют на прямые, косвенные, совокупные и совместные.

При прямом измерении искомое значение величины находят непо­средственно из опытных данных (например, измерение диаметра штан­генциркулем).

При косвенном измерении искомое значение величины определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям.

Совместными называют измерения двух или нескольких не одноимённых величин, производимые одновременно с целью нахождения функциональной зависимости между величинами (например, зависимости длины тела от температуры).

Совокупные – это такие измерения, в которых значения измеряемых величин находят по данным повторных измерений одной или нескольких одноименных величин (при различных сочетаниях мер или этих величин) путем решения системы уравнений.

3) По условиям, определяющим точность результата измерения, мето­ды делятся на три класса.

Измерении максимально возможной точности (например, эталонные измерения), достижимой при существующем уровне техники.

Контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторое заданное значение.

Технические измерения, в которых погрешность результата определяется характеристиками средств измерения.

4) По способу выражения результатов измерений различают абсолютные и относительные измерения.

Абсолютное измерение основано на прямых измерениях величины и (или) использования значений физических констант.

При относительных измерениях величину сравнивают с одноименной, играющей роль единицы или принятой за исходную (например, измерение диаметра вращающейся детали по числу оборотов соприкасающегося с ней аттестованного ролика).

5) В зависимости от совокупности измеряемых параметров изделия различают поэлементный и комплексный методы измерения.

Поэлементный метод характеризуется измерением каждого параметра изделия в отдельности (например, эксцентриситета, овальности, огранки цилиндрического вала).

Комплексный метод характеризуется измерением суммарного пока­зателя качества (а не физической величины), на который оказывают влияние отдельные его составляющие (например, измерение радиального биения цилиндрической детали, на которое влияют эксцентриситет, овальность и др.).

2. Методы измерений

Метод измерений – прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализо­ванным принципом измерений. Можно выделить следующие методы из­мерений.

По способу получения значения измеряемых величин различают два основных метода измерений.

Метод непосредственной оценки – метод измерения, при котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора прямого действия.

Метод сравнения с мерой – метод измерения, при котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.

Разновидности метода сравнения:

При измерении линейных величин независимо от рассмотренных методов различают контактный и бесконтактный методы измерений.

В зависимости от измерительных средств, используемых в процессе измерения, различают:

3. Понятие о точности измерений

Точность результата измерения – характеристика качества измерения, отражающая близость к нулю погрешности его результата.

Эти погрешности являются следствием многих причин: несовершенства средств измерений, метода измерений, опыта оператора; недостаточной тщательности проведения измерения; воздействия внешних условий и т.д. Для оценки степени приближения результатов измерения к истинному значению измеряемой величины используются методы теории вероятности и математической статистики, что позволяет с определенной достоверностью оценить границы погрешностей, за пределы которых они не выходят. Это дает возможность для каждого конкретного случая выбрать средства и методы измерения, обеспечивающие измерение результата, погрешности которого не превышают заданных границ с требуемой степенью доверия к результатам измерений (достоверностью).

Класс точности – обобщённая метрологическая характеристика средства измерения.

Класс точности определяется и обозначается по-разному. Наибольшее распространение получили три варианта, каждый представляет собой выраженное в процентах значение относительной погрешности:

– относительно измеренного значения (относительная погрешность),

– относительно максимального значения шкалы (приведённая погрешность),

– относительно участка шкалы (приведённая к участку шкалы погрешность).

Рассмотрим эти три варианта.

Вариант 1. Относительная погрешность.

Чтобы по классу точности определить значение абсолютной погрешности, результат измерения умножают на класс точности и делят на сто, чтобы избавиться от процентов. Например, вольтметром класса точности 0,1 получено значение 10,000 В.

Абсолютная погрешность составит: (10,000 В ∙ 0,1 %) / 100 % = 0,010 В. Запись результата: (10,000 ± 0,010) В, с вероятностью 95 % (эта вероятность по умолчанию назначается для технических измерений, исходя из этой вероятности определяется и класс точности). При нормировании по относительной погрешности, значение класса точности заключают в кружок. Как правило, обозначение класса точности размещают в правом нижнем углу на шкале средства измерений.

Вариант 2. Приведённая погрешность.

Чтобы по классу точности определить значение абсолютной погрешности, максимальное значение шкалы умножают на класс точности и делят на сто, чтобы избавиться от процентов. Например, вольтметром класса точности 0,1 получено значение 10,000 В. Максимальное значение шкалы составляет 20,000 В.

Абсолютная погрешность составит: (20,000 В ∙ 0,1 %) / 100 % = 0,020 В. Запись результата: (10,000 ± 0,020) В, с вероятностью 95 %. При нормировании по приведённой погрешности, значение класса точности не сопровождают никакими знаками.

Вариант 3. Приведённая к участку шкалы погрешность.

Чтобы по классу точности определить значение абсолютной погрешности, размер участка шкалы умножают на класс точности и делят на сто, чтобы избавиться от процентов. Рассмотрим два примера, для случая, когда вся шкала поделена на два участка.

Пример 1. Участок шкалы от 0,000 В до 12,000 В, отмечен галочкой. Вольтметром класса точности 0,1 получено значение 10,000 В.

Абсолютная погрешность составит: (12,000 В ∙ 0,1 %) / 100 % = 0,012 В. Запись результата: (10,000 ± 0,012) В, с вероятностью 95 %.

Пример 2. Участок шкалы от 12,000 В до 20,000 В, также отмечен галочкой. Вольтметром класса точности 0,1 получено значение 15,000 В.

Абсолютная погрешность составит: (8,000 В ∙ 0,1 %) / 100 % = 0,008 В. Запись результата: (15,000 ± 0,008) В, с вероятностью 95 %. При нормировании по приведённой к участку шкалы погрешности, значение класса точности помещают над галочкой. Участки шкалы, относительно которых нормируется погрешность, обозначают галочками.

Варианты классов точности обусловлены отличием конструктивных, системных и схемотехнических решений средств измерений.

Корректная запись результатов

Запись результатов измерений производится по следующим правилам.

1) Погрешность указывается двумя значащими цифрами, если первая равна 1 или 2. Погрешность указывается одной значащей цифрой, если первая равна 3 или более. Все остальные цифры должны быть не значащими.

Значащей цифрой называется любая цифра числа, записанного в виде десятичной дроби, начиная слева с первой отличной от нуля цифры, независимо от того, где она находится – до запятой или после запятой.

2) Результат измерения округляется в соответствии с его погрешностью, т.е. записывается с той же точностью, что и погрешность.

Рассмотрим пример. Результат измерения: 10,645701, погрешность 0,012908.

1) Рассматриваем погрешность. Первая значащая цифра 1, поэтому оставляем две значащие цифры, округляя, записываем: 0,013.

2) Рассматриваем результат измерения. Погрешность записана с точностью до третьего знака после запятой, поэтому в результате также оставим три знака. Округляя, записываем: 10,646.

Корректная запись: 10,646 ± 0,013.

Корректная запись обеспечивает адекватность и сопоставимость результатов различных измерений и является одним из элементов единства измерений. Как правило, отбрасывание избыточных цифр не приводит к дополнительной погрешности, поскольку избыточные цифры обусловлены точностью вычислений, а не точностью измерений.

4. Основы обеспечения единства измерений

Специализация и кооперирование производства в масштабах страны, основанные на принципах взаимозаменяемости, требуют обеспечения и сохранения единства измерений.

Обеспечение единства измерений – деятельность метрологических служб, направленная на достижение и поддержание единства измерений в соответствии с правилами, требованиями и нормами, установленными государственными стандартами и другими нормативно-техническими документами в области метрологии.

В 1993 г. был принят Закон Российской Федерации «Об обеспечении единства измерений», который устанавливает правовые основы обеспечения единства измерений в нашей стране. Он состоит из семи разделов: общие положения; единицы величин, средства и методики выполнения измерений; метрологические службы; государственный метрологический контроль и надзор; калибровка и сертификация средств измерений; ответственность за нарушение закона и финансирование работ по обеспечению единства измерений. В Законе дано следующее определение понятия «единство измерения»:

«Единство измерения – состояние измерений, при котором их результаты выражены в узаконенных единицах величин и погрешности измерений не выходят за установленные границы с заданной вероятностью».

Обеспечение единства измерений является задачей метрологических служб.

Метрологическая служба – совокупность субъектов, деятельности и видов работ, направленных на обеспечение единства измерений.

Закон определяет, что Государственная метрологическая служба находится в ведении Госстандарта России и включает: государственные научные метрологические центры; органы Государственной метрологической службы регионов страны, а также городов Москва и Санкт-Петербург.

Источник