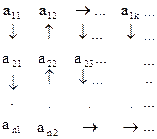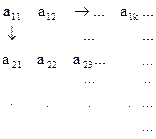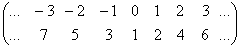Не более чем счетно
Счётные множества



Множество, равномощное множеству всех натуральных чисел, называется счётным.
Мощность множества натуральных чисел обозначается א0 = |N|.
Не более чем счётное множество – множество счётное или конечное.
Этим определением мы достали из класса эквивалентности, который назвали счётным, одного представителя – множество натуральных чисел – и теперь есть с чем сравнивать другие множества.
Любая биекция ν : N → M называется нумерацией множества М. М=
Таким образом, если найдена нумерация некоторого множества, то тем самым доказано, что оно счётное. Элементы счётного множества называют также последовательностью.
Пусть задан алфавит А – некоторое множество символов, называемых также буквами. Назовём словом в данном алфавите конечный ряд букв, написанных друг за другом. Иногда удобно рассматривать пустое слово, совсем не содержащее букв – его обозначают Λ.
Докажем, что в любом языке имеется счётное множество слов
Теорема. Если алфавит А конечен, то множество слов в алфавите А* счётно.
□. Пусть А=
Следствие: слов в алфавите <0,1,2,…,9>– счётное число. Это – проверка на корректность – мы снова подтвердили счётность множества натуральных чисел.
Теорема. Любое подмножество счётного множества не более чем счётно.
□ Пусть А – счетно. Значит, его элементы могут быть перенумерованы: <а1, а2, …, an,…>. Элементы любого подмножества ВÍА можно расположить в порядке возрастания номеров: 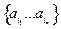
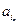
Теорема. Любое бесконечное множество содержит счётное подмножество.
Таким образом, по индукции мы построили множество, состоящее из попарно различных элементов <а1, а2, …, an,…>Î А0 с нумерацией ν(n)=an. ■
Из доказанных теорем следует, что счётное множество является самым минимальным по мощности из всех бесконечных множеств – потому, наверно, его и называют алеф ноль.
Теорема. В любом бесконечном множестве можно выделить два непересекающихся между собой счётных множества. Доказательство – разбиение на чётную и нечётную нумерации.
Семейство множеств
Теорема. Объединение любого не более чем счетного семейства множеств счётно.
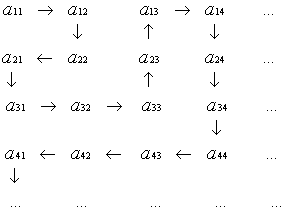
Занумеруем элементы объединения семейств следующим образом:
a) I конечно; б) I счетно
Последовательность (a11,a21,a12,a22,a31,…) – нумерация. Принцип её построения таков – сначала фиксируется N = 2 и записываются аik такие, что i+k = N. Затем N → N+1 и все повторяется.
Замечание: В семействах могут быть одинаковые элементы
Следствие. Множество А* всех слов в счётном алфавите А счётно. Пусть задана нумерация в А: A=<а1, а2, …, an,…>
Теорема. Множество значений функции, определённой на счётном множестве, не более чем счётно. ν(n) = f(an) – нумерация.
Теорема. Пусть А – бесконечное множество, а B – его не более чем счётное подмножество. Тогда, если множество A\B бесконечно, то оно равномощно множеству A.
Выберем из A\B счётное подмножество C; по построению B∩C =О. Объединение B и C счётно, поэтому существует биекция f : BÇC→C. Надо построить биекцию А→ A\B. Построим:
(А\ (BÇC))Ç(BÇC)= А→ A\B=(А\ (BÇC))ÇC
Следствие: если A бесконечно, а B не более чем счётно, то объединение AÇB не более чем счетно.
1.3.5. Мощности бесконечных множеств. Счетные множества
Определение. Говорят, что множества А и В имеют одинаковую мощность (или, что они равномощны), если между А и В можно установить биекцию. Множества, равномощные множеству натуральных чисел, называются Счетными.
Установить биекцию с множеством натуральных чисел N фактически означает: сопоставить каждому элементу рассматриваемого множества номер, т. е. пронумеровать все элементы, или другими словами – пересчитать.
Конечное или счетное множество называется Не более чем счетным.
Примеры и свойства счетных множеств.
· Множество четных чисел 2N – счетное. Действительно, биекцию 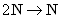
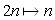
Задача гостинице “Бесконечность”.
В гостинице имеется счетное количество номеров, но все они заняты. Приехали еще 100 посетителей. Можно ли их разместить? А если приехали еще столько же, сколько уже имеется?
· Множество целых чисел Z счетно. Соответствующей биекцией, очевидно, является следующее отображение
· Объединение не более чем счетного множества счетных множеств – счетно.
Понятно, что при указанном способе рассмотрения элементов всякий элемент рано или поздно получит свой номер. Если 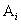
· Прямое произведение конечного числа счетных множеств – счетно.
Есть объединение счетного количества счетных множеств.
· Множество алгебраических чисел A (корней всевозможных многочленов с целыми коэффициентами) – счетно (докажите).
Разнообразие бесконечностей
Бесконечные множества содержат неограниченную последовательность элементов, объединенных общим признаком. Самые часто используемые из них в математике:
Все они бесконечны, вовсе не означает, что они равномощны.
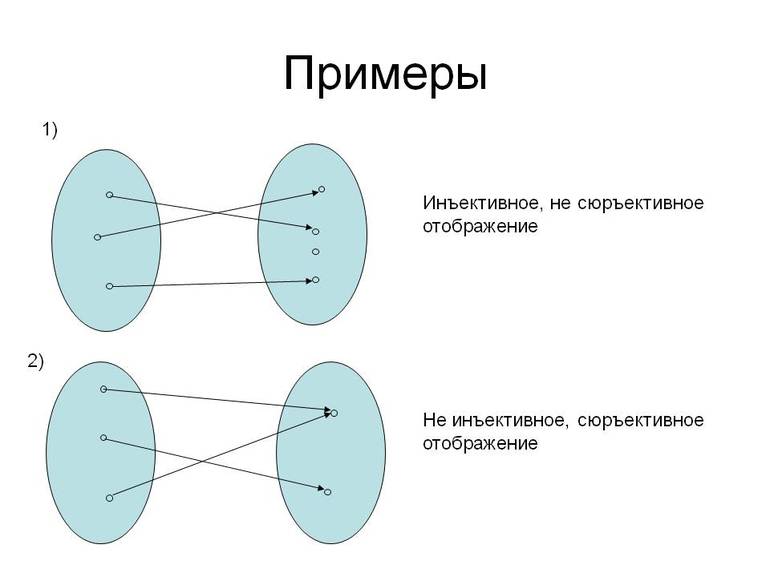
Сравнение и отображение
Числа в математике можно сравнивать друг с другом и выяснять, какое из них больше. С множествами можно производить аналогичные действия. Это будет называться их отображение друг в друга. Оно может быть дизъюнктивно, конъюнктивно и биективно. Это аналог числовых понятий «больше», «меньше» и «равно». Для того чтобы разобраться, как происходит это сравнение, нужно понятие подмножества.
Подмножеством некоторого набора компонентов называется любая часть компонентов этого набора. То есть, совокупность состоящее из чисел 1 и 3 является подмножеством множества чисел 1, 3 и 5. А они оба, в свою очередь, являются подмножествами совокупности нечётных чисел и т. д.
Если каждому компоненту множества A можно сопоставить какой-то элемент подмножества совокупности В, то отображение А в В конъюнктивно или А меньше, чем В. Если при этом нельзя найти в наборе А подмножество, которое можно сопоставить с совокупностью В, то отображение В в А дизъюнктивно. Если же каждому компоненту из комплекса А можно сопоставить элемент из совокупности В и каждому компоненту из набора В можно сопоставить элемент из совокупности А, то эти множества отображаются друг в друге биективно. В таком случае говорят, что они эквивалентны.
Для сравнения совокупностей можно использовать их мощность. Если мощность А меньше мощности В, то и множество А меньше, чем В. Если мощности равны, то сами наборы элементов эквивалентны.
Сопоставление наборов элементов
Казалось бы, используя свойства сравнения наборов элементов, можно найти соотношение мощностей бесконечных совокупностей. Ведь очевидно, что множество N является подмножеством совокупности Z, они оба являются подмножеством Q, а множества Q и I вместе составляют R. И отсюда, по определению, следует, что мощности соотносятся так: |N| |I|, и загадкой остается только соотношение совокупностей Q и I. Но всё не так просто.
Выяснение размера бесконечного комплекса компонентов — такая же задача, как определение размера конечной совокупности — пересчёт компонентов. Возможность посчитать и пронумеровать элементы бесконечной совокупности называется счётностью. Совокупность натуральных чисел — счётная. Элементам в этом случае легко присвоить порядковые номера. И все множества, которые эквивалентны N, тоже будут счётными. Его размер |N| = a.
Но если взять R, то его элементы пронумеровать не получится. Ведь между любыми двумя точками, а прямой всегда можно поставить ещё одну. То есть, совокупность R «бесконечна вглубь»: каждый промежуток между бесконечным количеством точек содержит в себе бесконечное количество точек. Значит, свойство R — несчётность. Такие «бесконечные вглубь» множества называют континуальными. И их мощность обозначается как |R| = c.
Ещё одно важное свойство бесконечных множеств заключается в том, что если из бесконечной совокупности удалить (или добавить к ней) подмножество меньшей мощности, то размер исходной совокупности сохранится. Если из N убрать все числа от 1 до 10, то его мощность не уменьшится на 10, а останется прежней. Множество останется бесконечным и счётным: a — 10 = a.
Бесконечная мощность счётных и несчётных множеств может быть описана тремя формулами. Это два равенства и одно неравенство:
Совокупность всех точек интервала или отрезка на прямой тоже будет континуальна, так как на неё можно спроецировать всю совокупность точек действительной прямой R.
Соотношение мощностей
Континуальное множество больше счётного. Но какова их разница? Чтобы это вычислить, потребуется понятие булеан.
Что такое булеан
Есть некий набор компонентов V. Булеаном V будет называться комплекс всех его подмножеств. Как будут соотноситься размер булеана и самого V? Если V состоит из одного элемента, то его булеан будет состоять из двух элементов: пустого набора компонентов и самого V. Если V состоит из двух элементов, то булеан содержит 4 элемента: пустое множество, V и каждый из двух элементов. Если V содержит 3 элемента, то булеан содержит 8: пустое, само V, каждый из трёх его элементов в отдельности и каждую пару элементов (которых тоже три).
То есть мощность булеана — это 2 в степени размера самого V. Булеан так и записывается 2^|V|. Размер булеана всегда будет больше, чем мощность самой совокупности.
Результат сопоставления
Размер булеана любой счётной совокупности будет 2^a. Если рассматривать N, то его булеан будет состоять из пустоты, бесконечного числа элементов N, бесконечного числа пар элементов, бессчётного числа сочетаний элементов по 3, 4, 5 и так до бесконечности. Какому известному множеству можно сопоставить этот булеан?
Так как это N — натуральные числа, то каждый элемент булеана — это последовательность чисел. Если представить каждую такую последовательность в виде знаков после запятой в десятичной дроби, то получатся координаты точек в интервале от 0 до 1, который эквивалентен R. Так как булеан N содержит бесконечное количество комбинации бесконечных десятичных дробей, то он покрывает все точки в этом интервале. Это нестрогое доказательство уравнения c = 2^a.
Обозначения мощностей а и c происходят от слов account и continum, но именно такая последовательность букв порождает вопрос: а есть ли бесконечное множество мощностью b, которое меньше c, но больше a. Если и есть, то пока они неизвестны. А вот комплекс больший по мощности, чем c, есть. Это булеан континуального множества с мощностью 2^c. А у этого булеана тоже есть булеан с ещё большей мощностью.
Бесконечные множества бывают счётными и несчётными. Счётными называют те, элементы в которых можно пересчитать, то есть эквивалентные совокупности натуральных чисел. К ним относятся само множество натуральных, а также целых и рациональных чисел. Среди несчётных выделяют континуальные множества, эквивалентные совокупности всех точек на прямой. К ним относятся действительные и иррациональные числа. Континуальность является булеаном счётного набора.
06. Теоремы о счетных множествах. Множества мощности континуум
Если рассмотреть любое конечное множество и любое его собственное (непустое и не совпадающее с ним самим) подмножество, то элементов в подмножестве меньше, чем в сам множестве, т. е. часть меньше целого.
Обладают ли бесконечные множества таким свойством? И может ли иметь смысл утверждение, что в одном бесконечном множестве «меньше» элементов, чем в другом, тоже бесконечном? Ведь про два бесконечных множества мы можем пока только сказать, эквивалентны они или нет. А существуют ли вообще неэквивалентные бесконечные множества?
Приведём забавную фантастическую историю из книги Н. Я. Виленкина «Рассказы о множествах». Действие происходит в далёком будущем, когда жители разных галактик могут встречаться друг с другом. Поэтому для всех путешествующих по космосу построена огромная гостиница, протянувшаяся через несколько галактик.
В этой гостинице бесконечно много номеров (комнат), но, как и положено, все комнаты пронумерованы, и для любого Натурального числа n есть комната с этим номером.
Однажды в этой гостинице проходил съезд космозоологов, в котором участвовали представители всех галактик. Так как галактик тоже бесконечное множество, все места в гостинице оказались занятыми. Но в это время к директору гостиницы приехал его друг и попросил поселить его в эту гостиницу.
«После некоторых размышлений директор обратился к администратору и сказал:
– Куда же я дену жильца этого номера? – удивлённо спросил администратор.
– А его переселите в № 2. Жильца же из № 2 отправьте в № 3, из № 3 – в № 4 и т. д.»
Вообще, пусть постоялец, живущий в номере K, переедет в номер K+1, как это показано на следующем рисунке:
Тогда у каждого снова будет свой номер, а № 1 освободится.
Таким образом, нового гостя удалось поселить – именно потому, что номеров в гостинице бесконечно много.
Первоначально участники съезда занимали все номера гостиницы, следовательно, между множеством космозоологов и множеством N Было установлено взаимно однозначное соответствие: каждому космозоологу дали по номеру, на двери которого написано соответствующее ему натуральное число. Естественно считать, что делегатов было «столько же», сколько имеется натуральных чисел. Но приехал ещё один человек, его тоже поселили, и количество проживающих увеличилось на 1. Но их снова осталось «столько же», сколько и натуральных чисел: ведь все поместились в гостиницу!
Мы пришли к удивительному выводу: если к множеству, которое равномощно N, добавить ещё один элемент, получится множество, которое снова равномощно N. Но ведь совершенно ясно, что делегаты-космозоологи представляют собой часть того множества людей, которые разместились в гостинице после приезда нового гостя. Значит, в этом случае часть не «меньше» целого, а «равна» целому!
Итак, из определения эквивалентности (которое не приводит ни к каким странностям в случае конечных множеств) следует, что часть бесконечного множества может быть эквивалентна всему множеству.
Новый постоялец не удивился, когда на другое утро ему предложили переселиться в № 1000000. Просто в гостиницу прибыли запоздавшие космозоологи из галактики ВСК-3472, и надо было разместить ещё 999999 жильцов.
Эта задача оказалась весьма сложной. Но и в этом случае нашёлся выход.
«В первую очередь администратор приказал переселить жильца из № 1 в № 2.
– А жильца из № 2 переселите в № 4, из № 3 – в № 6, вообще, из номера N – в номер 2n.
Определение. Множество А, равномощное множеству натуральных чисел N, называется Счетным множеством (имеет мощность счетного множества). Если множество В является бесконечным и не равномощно множеству N, то его называют несчетным.
Множество, которое является конечным или счетным, еще называют не более чем счетным .
Пусть множество А является счетным. По определению, тогда существует биекция А на N, т. е. каждому аÎА соответствует единственный номер nÎN и множество А обращается в некоторую последовательность <аn>.
Теорема 1. Любое подмножество счетного множества не более чем счетно.
Доказательство. Пусть А = 

Теорема 2. Объединение конечного или счетного числа счетных множеств является счетным множеством.
Теорема 3. Любое бесконечное множество содержит счетное подмножество.
Доказательство. Выберем в заданном множестве А какой-либо элемент, придав ему единичный индекс: а1. Среди всех оставшихся элементов множества А найдется не равный а1 элемент (в силу бесконечности А). Его мы обозначим через а2. Продолжая этот процесс до бесконечности мы получим необходимое нам счетное множество
Доказательство. Пусть множество М – А не более чем счетно. Тогда множество М = АÈ(М – А) по теореме 2 не более чем счетно. Это противоречит тому, что множество М несчетно и, следовательно, наше исходное предположение не верно. Таким образом, множество М – А несчетно. Последнее еще не означает равномощности множеств М и М – А. Докажем ее. Выделим из М – А счетное множество В. Обозначим через С множество С = (М – А) – В. Справедливы равенства М = АÈВÈС и М – А = ВÈС. Множество АÈВ счетно (теорема 2). Следовательно, существует биекция f из АÈВ на А. Теперь можно построить биекцию g из М на М – А по правилу:
Теорема 5. Если множество С бесконечно, а В не более чем счетно, то множество ВÈС равномощно множеству С.
Доказательство. Если множество С счетно, то множество ВÈС также счетно и следовательно они равномощны. Если же множество С не счетно, то мы можем воспользоваться теоремой 4, положив в ней А = СÇВ, а М = С.
Теорема 6. Если множество С является бесконечным, то существует его подмножество В такое, что В¹С и В равномощно с С.
Доказательство. По теореме 3 мы можем выделить из множества С его счетное подмножество А. Если множество С счетно, то в качестве В из утверждения теоремы можно взять В=А. Если же С не счетно, то можно положить В=С-А и утверждаемое вытекает из теоремы 4.
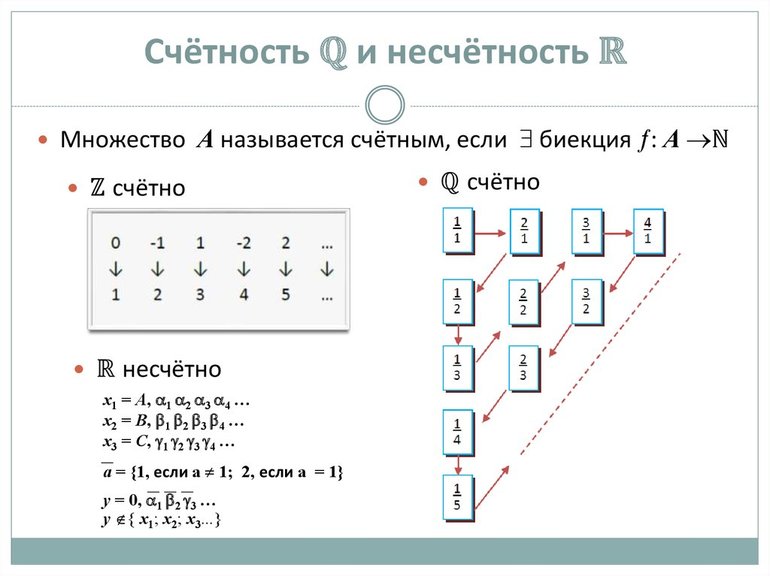
Теорема 7. Множество рациональных чисел Q является счетным.
Доказательство. Обозначим через Р множество всех пар натуральных чисел (p, q), таких что p и q не имеют общих целых делителей, кроме единицы. Для пары натуральных чисел (p, q) введем ее высоту m = p + q. Обозначим Рn множество пар натуральных чисел высоты n. Нетрудно проверить, что каждое множество Рn является конечным и содержит не более, чем n-1 член. Так как Р = Èn Рn, то множество Р счетно в силу теоремы 2.
Теорема 8. Множество точек интервала (0,1) является несчетным.
Доказательство (Диагональный метод Кантора). Доказательство проведем от противного, предположив, что множество точек интервала (0,1) является счетным. Тогда все точки можно записать в виде последовательности:
Множества, равномощные множеству точек интервала (0, 1), называются множествами мощности Континуум .
Задачи.
1. Показать, что если множества А и В являются счетными, то и их произведение А´В является счетным.
2. Установить биекцию между множеством N всех натуральных чисел и множеством Q всех четных положительных чисел.
3. Установить биекцию между множеством N всех натуральных чисел и множеством Р всех четных чисел.
Счетные множества
Множество называется счетным, если оно равномощно множеству 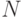




Например, множество целых чисел 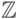






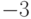
(а) Подмножество счетного множества конечно или счетно.
(в) Объединение конечного или счетного числа конечных или счетных множеств конечно или счетно.
(а) Пусть 
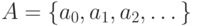
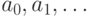



(в) Пусть имеется счетное число счетных множеств 
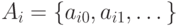
Замечание. В доказательстве утверждения (б) теоремы 2 есть тонкий момент: на каждом шаге мы должны выбрать один из оставшихся элементов множества 
30. Такой же тонкий момент (хотя и менее очевидный) есть и в доказательстве утверждения (в). Можете ли вы догадаться, где он? (Ответ: мы знаем, что множества 
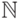


Еще несколько примеров счетных множеств:
31. Докажите, что любое семейство непересекающихся интервалов на прямой конечно или счетно. (Указание: в каждом интервале найдется рациональная точка.)
33. Докажите, что множество точек строгого локального максимума любой функции действительного аргумента конечно или счетно.
Докажите, что множество точек разрыва неубывающей функции Действительного аргумента конечно или счетно.