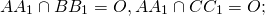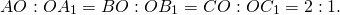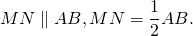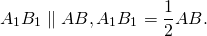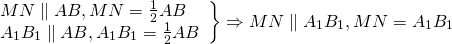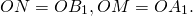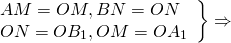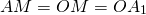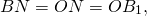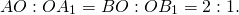Как доказать что медианы пересекаются в одной точке

Свойство медиан треугольника

Свойство медиан треугольника может быть доказано многими способами. Доказательство, опирающееся на свойства параллелограмма и средней линии треугольника, может быть проведено сразу же после изучения соответствующих тем, что позволяет начать использовать свойство медиан треугольника уже с начала 8 класса.

(Свойство медиан треугольника)

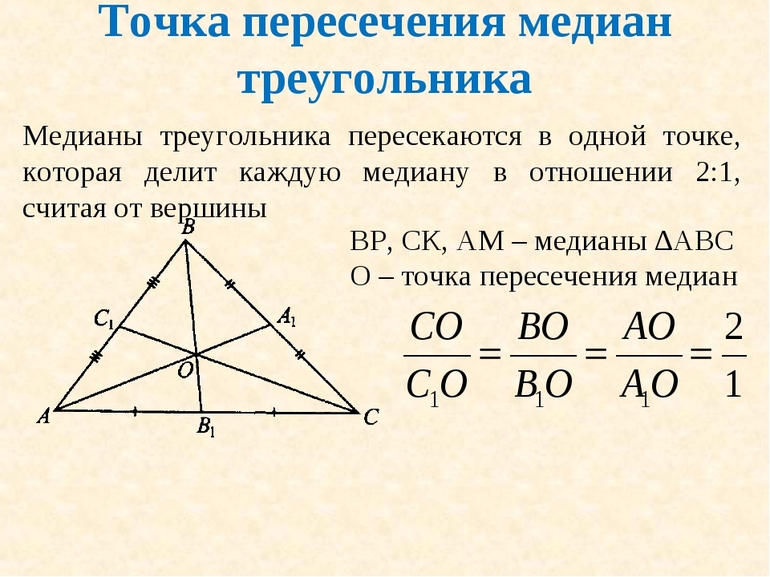
Медианы треугольника пересекаются и в точке пересечения делятся в отношении 2:1, считая от вершины.

Дано : ABC, AA1, BB1, CC1 — медианы

1) Пусть M — середина отрезка AO, N — середина BO

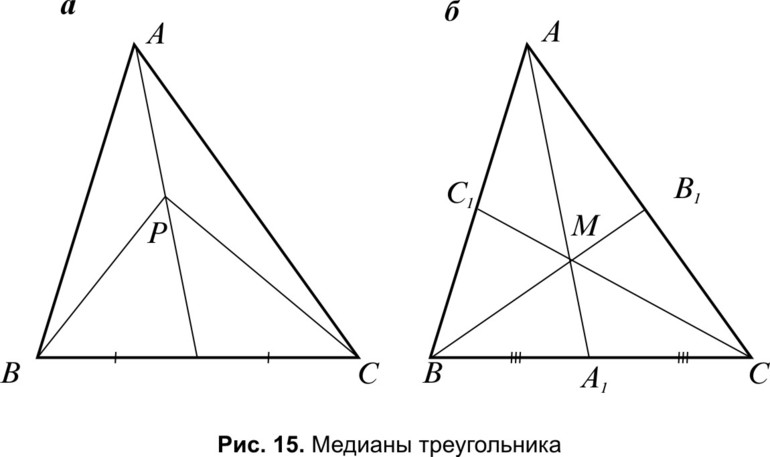
2) Соединим точки M, N, A1 и B1 отрезками.

3) Так как AA1 и BB1 — медианы треугольника ABC, точка A1- середина отрезка BC, B1 — середина AC.

Следовательно, A1B1 — средняя линия треугольника ABC и

Значит, четырёхугольник MNA1B1 — параллелограмм (по признаку).

По свойству диагоналей параллелограмма

из чего следует, что

5) Доказательство того факта, что все медианы треугольника пересекаются в одной точке, будем вести методом от противного.

Предположим, что третья медиана CC1 треугольника ABC пересекает медианы AA1 и BB1 в некоторой точке, отличной от точки O.

Тогда на каждой медиане есть две различные точки, делящие её в отношении 2:1, считая от вершины. Пришли к противоречию.

Таким образом, все три медианы треугольника пересекаются в одной точке и точка пересечения медиан делит каждую из их в отношении 2:1, считая от вершины:

7 Comments

Промогите пожалуйста:
В прямоугольном треугольнике из вершины прямого угла до гипотенузы провели медиану длинной 50см и перпендикуляр 48см. Вычислить периметр.

Медиана, проведённая к гипотенузе, равна её половине. Следовательно, гипотенуза 100 см. Пусть катеты равны x см и y см. По теореме Пифагора x²+y²=100². Площадь треугольника равна половине произведения стороны на высоту, проведённую к этой стороне S=0,5∙100∙48 см², либо половине произведения катетов S=0,5∙x∙y. Отсюда xy=4800.
Решаем систему уравнений: x²+y²=100²; xy=4800. Решения (60;80) (80;60). То есть катеты 60 см и 80 см. Периметр P=60+80+100=240 см.
(Не обязательно доводить решение системы до конца. Достаточно найти x+y. Для этого к 1-му уравнению прибавим удвоенное 2-е, получим
x²+2xy+y²=19600; x+y=140).

Прошу помощи в решении задачи: на стороне ромба построен равносторонний треугольник. Отрезок, соединяющий точку пересечения диагоналей ромба с серединой стороны треугольника, составляет с ней угол 70 градусов. Найти острый угол ромба.

Во-первых, большое спасибо за решение, даже не ожидала ответа, но, по счастью, ошиблась! Но я к этому времени уже решила так:провела ВМ, которая в равностороннем треугольнике является также высотой.
Рассмотрим четырехугольник ОВМС: угол ВОС =углу ВМС=90 градусов (диагонали ромба взаимно перпендикулярны),отсюда, ВМ параллельна ОС, тогда угол МОС=20 градусам. Рассм. треугольник ОМС: угол МСО= 180-20-70=90 градусов, и одновременно= 60+x, т.о., угол х=30 градусам, и искомый острый угол ромба=60 градусам. Мы получили разные ответы, в чем может быть дело (окружности мы еще не проходили).

Наталия углы BOC и BMC не накрест лежащие и не внутренние односторонние, поэтому BM не параллельна OC. Но вариант решения без окружности возможен, добавила второй способ.

Источник

Свойства медианы треугольника (ЕГЭ 2022)

Сегодня мы рассмотрим часть треугольника, которая не раз поможет тебе при решении многих задач, — медиану.

Эта приятная, лёгкая и полезная теория!

Медиана треугольника — коротко о главном

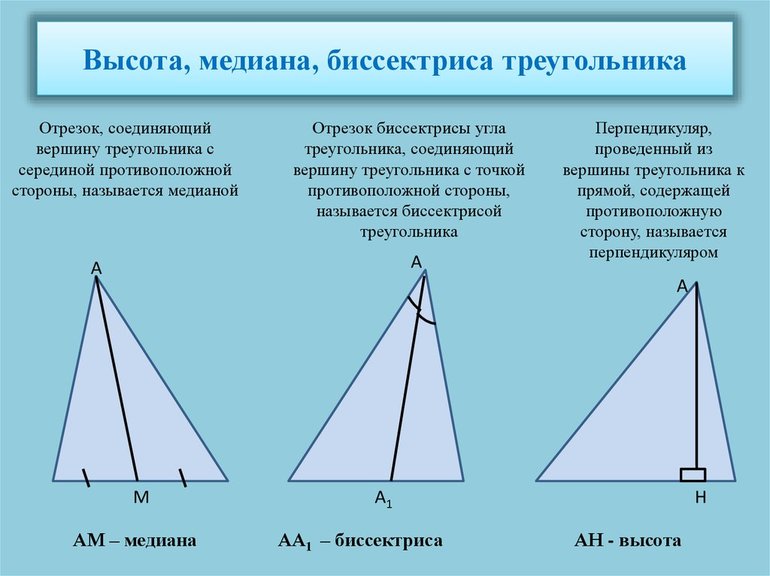
Медиана — отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Медиана делит площадь треугольника пополам

Но \( \displaystyle AM=CM\), значит, \( \displaystyle <_<\triangle ABM

Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении \( \displaystyle 2:1\ \), считая от вершины.

Но \( \displaystyle AM=CM\), значит, \( \displaystyle <_<\triangle ABM

Длина медианы: \( \displaystyle <^<2>>=\frac <1>

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.

Если медиана равна половине стороны, то треугольник прямоугольный и эта медиана проведена к гипотенузе.

Определение медианы треугольника

Это очень просто! Возьми треугольник.

Отметь на какой-нибудь его стороне середину \( \displaystyle M\).

И соедини с противоположной вершиной!

Получившийся отрезок \( \displaystyle BM\) и есть медиана.

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Медиана в прямоугольном треугольнике

Медиана равна половине гипотенузы прямоугольного треугольника!

Почему. При чём тут прямой угол?

Давай смотреть внимательно. Только не на треугольник, а на … прямоугольник.

Ты заметил, что наш треугольник \( \displaystyle ABC\) – ровно половина этого прямоугольника?

Проведём диагональ \( \displaystyle BD\):

Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам?

Но одна из диагоналей – \( \displaystyle AC\) – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы \( \displaystyle \Delta ABC\).

Она называлась у нас \( \displaystyle M\).

Значит, половина второй диагонали – наша медиана \( \displaystyle BM\). Диагонали равны, их половинки, конечно же, тоже. Вот и получим \( \displaystyle BM=MA=MC\)

Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.

Более того, так бывает только в прямоугольном треугольнике!

Если медиана равна половине стороны, то треугольник прямоугольный, и эта медиана проведена к гипотенузе.

Доказывать это утверждение мы не будем, а чтобы в него поверить, подумай сам: разве бывает какой-нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника?

Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике.

Решение задач на свойства медианы в прямоугольном треугольнике

Давай посмотрим, как это свойство помогает решать задачи.

Задача №1:

В \( \displaystyle \Delta ABC\) стороны \( \displaystyle AC=5\); \( \displaystyle BC=12\). Из вершины \( \displaystyle C\) проведена медиана \( \displaystyle CN\).

Найти \( \displaystyle AB\), если \( \displaystyle AB=2CN\).

Сразу вспоминаем, это если \( \displaystyle CN=\frac<2>\), то \( \displaystyle \angle ACB=90<>^\circ \)!

Ура! Можно применить теорему Пифагора!

Видишь, как здорово? Если бы мы не знали, что медиана равна половине стороны только в прямоугольном треугольнике, мы никак не могли бы решить эту задачу. А теперь можем!

Применяем теорему Пифагора:

А в следующей задаче пусть у нас будет не одна, а целых три медианы! Как же они себя ведут?

Запомни очень важный факт:

Три медианы в треугольнике (любом!) пересекаются в одной точке и делятся этой точкой в отношении \( 2:1\), считая от вершины.

Сложно? Смотри на рисунок:

Медианы \( \displaystyle AM\), \( \displaystyle BN\) и \( \displaystyle CK\) пересекаются в одной точке.

Задача №2:

Решение:

\( \displaystyle \angle B=90<>^\circ \) – треугольник прямоугольный!

(Применили то, что медиана, проведённая к гипотенузе равна половине гипотенузы).

Найдём \( \displaystyle AC\) по теореме Пифагора:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Теорема о медиане и площади треугольника

Медиана делит площадь треугольника пополам

Почему? А давай вспомним самую простую форму площади треугольника. \( S=\frac<1><2>a

И применим эту формулу аж два раза!

Посмотри, медиана \( \displaystyle BM\) разделила \( \displaystyle \triangle ABC\) на два треугольника: \( \displaystyle \triangle ABM\) и \( \displaystyle \triangle BMC\).

Но! Высота-то у них одна и та же – \( \displaystyle BH\)!

Только в \( \displaystyle \triangle ABM\) эта высота \( \displaystyle BH\) опускается на сторону \( \displaystyle AM\), а в \( \displaystyle \triangle BMC\) – на продолжение стороны \( \displaystyle CM\).

Удивительно, но вот бывает и так: треугольники разные, а высота – одна. И вот, теперь-то и применим два раза формулу

1) B \( \displaystyle \triangle ABM\):

«\( \displaystyle a\)» – это \( \displaystyle AM\) «\( \displaystyle h\)» – это \( \displaystyle BH\)

\( \displaystyle \Rightarrow <_<\triangle ABM>>=\frac <1> 2) B \( \displaystyle \triangle BMC\): «\( \displaystyle a\)» – это \( \displaystyle CM\) «\( \displaystyle h\)» – это опять \( \displaystyle BH\) \( \displaystyle \Rightarrow <_<\triangle BMC>>=\frac <1> Читать далее… Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Теорема о трех медианах треугольника Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении \( \displaystyle 2:1\ \), считая от вершины. Что бы это такое значило? Посмотри на рисунок. На самом деле утверждений в этой теореме целых два. Ты это заметил? 1. Медианы треугольника пересекаются в одной точке. 2. Точкой пересечения медианы делятся в отношении \( \displaystyle 2:1\ \), считая от вершины. Давай попробуем разгадать секрет этой теоремы, то есть доказать ее. Доказательство теоремы о трех медианах треугольника Сначала проведем не все три, а только две медианы. Они-то уж точно пересекутся, правда? Обозначим точку их пресечения буквой \( \displaystyle E\). Соединим точки \( \displaystyle N\) и \( \displaystyle K\). Что получилось? Конечно, \( \displaystyle NK\) – средняя линяя \( \displaystyle \triangle ABC\). Ты помнишь, что это значит? А теперь проведем ещё одну среднюю линию: отметим середину \( \displaystyle AE\) – поставим точку \( \displaystyle F\), отметим середину \( \displaystyle EC\) — поставим точку \( \displaystyle G\). Теперь \( \displaystyle FG\) – средняя линия \( \displaystyle \triangle AEC\). То есть: Что из этого следует? Посмотри теперь на четырехугольник \( \displaystyle NKGF\). У какого четырехугольника противоположные стороны (\( \displaystyle NK\) и \( \displaystyle FG\)) параллельны и равны? Конечно же, только у параллелограмма! Значит, \( \displaystyle NKGF\) – параллелограмм. Ну и что? А давай вспомним свойства параллелограмма. Например, что тебе известно про диагонали параллелограмма? Правильно, они делятся точкой пересечения пополам. Снова смотрим на рисунок. Читать далее… Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз: Формула длины медианы треугольника Как же найти длину медианы, если известны стороны? А ты уверен, что тебе это нужно? Откроем страшную тайну: эта формула не очень полезная. Но всё-таки мы её напишем, а доказывать не будем. Итак, \( \displaystyle <^<2>>=\frac <1> Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике по треугольникам Лучше всего смотреть это видео с ручкой и тетрадкой в руках. То есть ставьте видео на паузу и решайте задачи самостоятельно. Помните, понимать и уметь решать — это два, совершенно разных навыка. Очень часто вы понимаете как решить задачу, но не можете это сделать. Или допускаете ошибки, или просто теряетесь и не можете найти ход решения. Как с этим справиться? Нужно решать много задач. Другого способа нет. Вы должны совершить свои ошибки, чтобы научиться их не допускать. ЕГЭ №6 Равнобедренный треугольник, произвольный треугольник В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ. Очень часто все «проблемы» с решением задач на равнобедренный треугольник решаются построением высоты. Также мы научимся решать и «обычные» треугольники. ЕГЭ №6 Прямоугольный треугольник, теорема Пифагора, тригонометрия Большинство задач в планиметрии решается через прямоугольные треугольники. Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных. Но на уроках этой темы мы убедимся, что это действительно так. Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше. И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными. В этом видео мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии. ЕГЭ №16. Подобие треугольников. Задачи н доказательство Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников! Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства. Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы. В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение. Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем. Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач. Источник Общие сведения Перед доказательством теорем необходимо ознакомиться с основными понятиями. Прямой называется совокупность точек, расположенных в одной плоскости, через которые можно провести линию без искажений в пространстве. Отрезок — часть прямой, ограниченной правой и левой границами. Треугольник (обозначается «Δ») — геометрическая фигура, состоящая из трех сторон и вершин. Предпоследние являются отрезками, а последние — точками, не лежащими на одной прямой и соединяющими стороны между собой. Следует отметить, что треугольники бывают нескольких типов. К ним относятся следующие: Первая группа состоит из сторон различной длины. При двух эквивалентных между собой сторонах фигура является равнобедренной. Обязательным условием для третьей группы считается равенство всех сторон. Кроме того, фигуры делятся по типу градусных мер таким образом: Остроугольным называется треугольник, у которого углы (в задачах обозначается символом «∠ «) меньше 90 градусов. Если у него один из ∠ эквивалентен 90, то этот признак свидетельствует о принадлежности его ко второму типу. Когда у фигуры хотя бы один из ∠ больше 90, тогда он принадлежит к третьему виду. Понятие дополнительных отрезков У любого Δ существуют дополнительные отрезки, которые используются при решении задач по геометрии. К ним относятся следующие: медиана, биссектриса и высота. Они существенно отличаются между собой в произвольных треугольниках, а также совпадают в равнобедренных и правильных геометрических телах. Медиана (М) — некоторый отрезок, исходящий из вершины на середину стороны. Иными словами, любой геометрический элемент, опущенный из вершины на среднюю точку, является медианой. Последних в треугольнике может быть не более трех. Биссектриса (Б) — часть прямой, которая делит угол на два равных компонента. В любом треугольнике можно провести всего три таких отрезка. Высота (В) — перпендикуляр, опущенный из вершины на противоположную сторону. Следует отметить, что высоты бывают внешними и внутренними. Первые проводятся из вершины на проекцию Δ, а вторые находятся внутри фигуры. В каждом треугольнике можно провести определенное количество дополнительных отрезков: Во втором случае М, В и Б совпадают между собой только один раз, а в последнем — полное сходство, поскольку медианы являются биссектрисами и высотами. Их точка пересечения — центр треугольника. Далее следует перейти к непосредственному доказательству теорем. Теорема о взаимном пересечении Первую базовую теорему, которую следует разобрать, имеет такую формулировку: медианы любого треугольника пересекаются в одной точке, которая является центром фигуры. Ее доказательство осуществляется по такому алгоритму: Аналогично можно доказать, что медиана UU’ также пересекается с SS’ и TT’ в точке F. Для этой цели необходимо начертить еще один треугольник с таким же обозначением, т. е. ΔSTU. После этого выполнить все пять пунктов алгоритма, но для медиан SS’ и UU’. Затем сопоставить два доказательства для получения общей формулировки. Утверждения о соотношении Однако для решения задач одной теоремы о пересечении медиан недостаточно. Математики доказали несколько других утверждений, которые могут быть полезными при нахождении неизвестных величин. Первая из них гласит, что точка, в которой пересекаются медианы, пропорционально делит медианы 2:1 относительно вершины. Для доказательства утверждения необходимо воспользоваться такой методикой: Следующим полезным утверждением является формула, позволяющая найти длину медианы. Она в словесном эквиваленте звучит таким образом: длина равна квадратному корню из суммы половины квадратов двух других сторон, не принадлежащих ей, без четвертой части квадрата стороны, на которую она опущена. Для доказательства рекомендуется использовать такой алгоритм: Теорема имеет следствие, представленное в виде соотношения, позволяющее выявить взаимосвязь между сторонами и медианами. Оно имеет такой вид: (М)^2 + (М)^2 + (М)^2=3/4(s^2+t^2+u^2). Координаты точки При решении задач очень часто необходимо находить координаты точки пересечения медиан произвольного ΔSTU. Доказательство или выведение этой формулы является очень сложным. Однако математики решили данную проблему. Они предлагают использовать уже готовое соотношение, состоящее из двух компонентов: Вышеописанные формулы рекомендуется применять, когда требуется определить координаты точек без чертежа. Специалисты на ранних этапах обучения рекомендуют размещать треугольник в прямоугольной декартовой системе координат. После этого отмечать каждую вершину с заданными координатами, а затем проводить медианы. Для нахождения величины абсциссы и ординаты нужно из искомой точки опускать перпендикуляры на последние. Нахождение координаты будет очень простым и удобным. Кроме того, в интернете существует множество приложений для этих целей. Они называются онлайн-калькуляторами. Иногда встречаются задания со следующей формулировкой: выведите формулы, выражающие координаты точки пересечения медиан, с исходными данными (вершинами или сторонами). Для этого рекомендуется просто подставить искомые значения в соответствующие формулы нахождения абсциссы и ординаты. Полезные свойства Математики для облегчения учебы вывели важные свойства медианы. К ним относятся следующие: На координатной плоскости, руководствуясь первым свойством, чертится треугольник. После этого требуется провести две медианы, обозначив общую точку (где они пересекаются). Далее необходимо поставить в нее иголку циркуля, и начертить окружность вокруг фигуры. Затем в искомом круге проводится диаметр D. В результате у вписанной окружности величина радиуса должна соответствовать значению D/4. На основании этого необходимо полагать, что построение выполнено правильно. В противном случае допущена некоторая неточность. Используя второе свойство, можно найти следующие параметры: площадь, стороны и другие элементы фигуры. В любых задачах допускается подобное дополнительное построение. Однако специалисты рекомендуют его применять только при необходимости, а не загромождать чертеж. Третье и четвертое свойства применяются для подсчета площадей подобных фигур. Коэффициент подобия зависит от количества проведенных медиан: Последние цифры являются коэффициентом подобия. В прямоугольном треугольнике медиана, опущенная из прямого угла, делит ее на две равные части-радиусы описанной окружности. Таким образом, сведения о медианах в треугольнике расширяет возможности расчета некоторых параметров фигуры. Источник ← Навыки фасилитации что это Мужская сумка тоут с чем носить → Вам также понравится Металлоплакирующая смазка что это 22.10.202314.06.2023 admin 0 Как детям объяснить что такое радуга 19.10.202311.06.2023 admin 0 К чему снятся черные волосы на голове у себя 17.10.202311.06.2023 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Δ