Как доказать что множество континуум
Тут же можно задать и другой вопрос, а континуальной ли множество НЕВОЗРАСАЮЩИХ бесконечных последовательностей натуральных чисел? Почему?
задан 16 Ноя 14:31
1 ответ
Первый из вопросов представляется несколько странным. Дело в том, что если мы возьмём ВСЕ последовательности натуральных чисел, то их будет континуум. Это отображения из N в N, их мощность равна N^N. Это не больше, чем (2^N)^N
2^N, то есть континуум (оценка сверху). С другой стороны, если оставить только строго возрастающие, то их не меньше континуума. Мы каждый следующий член можем увеличивать на 1 или на 2. Достаточно рассматривать только такие объекты, потому что их уже будет 2^N. Понятно, что невозрастающих будет по мощности не меньше, однако больше континуума быть не может по причине верхней оценки.
В тех случаях, когда мы хотим иметь более явную биекцию, нам совершенно нет разницы, с каким множеством мы имеем дело. А именно, если a1 =1, а во втором они >=0. Вычитая из каждого по единице, мы строим явную биекцию между множеством возрастающих и множеством неубывающих. Хотя для такой задачи это уже лишнее.
Если говорить о множестве невозрастающих последовательностей, то оно счётно. Всякая такая последовательность стабилизируется на некотором числе, то есть фактически она конечна. А конечных последовательностей только счётное множество, что можно доказать многими способами (даже при помощи явно задаваемой нумерации).
отвечен 16 Ноя 20:54
@falcao. Доказываю континуальность неуб.послед. Уточняющий вопрос. Т.е, если мы рассматриваем неубывающую последовательность, мы строим последовательность. a1, a2-a1, a3-a2. Вычитам по единичке и у нас получается биекция?
@vivalavida: по-моему, Вы пытаетесь делать что-то лишнее. При помощи используемого приёма можно построить биекцию между множеством всех последовательностей натуральных чисел, и множеством неубывающих. Но это нигде не требуется в условии. Достаточно доказать, что возрастающих последовательностей МНОГО, то есть континуум. А это делается при помощи прибавления то 1, то 2. Неубывающих будет ещё больше.
Множества мощности континуума



Существуют бесконечные множества, элементы которых нельзя перенумеровать. Такие множества называются несчетными.
Теорема Кантора. Множество всех точек отрезка [0, 1] несчетно.
Множество, эквивалентное множеству всех точек отрезка [0, 1] называется множеством мощности континуума.
Так как множества точек интервалов, отрезков и всей прямой эквивалентны между собой, то все они имеют мощность континуума.
Чтобы доказать, что данное множество имеет мощность континуума, достаточно указать взаимно однозначное соответствие между данным множеством и множеством точек отрезка, интервала или всей прямой.
Из рис. 1.8 следует, что множество точек параболы y = x 2 эквивалентно множеству точек прямой –¥
06. Теоремы о счетных множествах. Множества мощности континуум
Если рассмотреть любое конечное множество и любое его собственное (непустое и не совпадающее с ним самим) подмножество, то элементов в подмножестве меньше, чем в сам множестве, т. е. часть меньше целого.
Обладают ли бесконечные множества таким свойством? И может ли иметь смысл утверждение, что в одном бесконечном множестве «меньше» элементов, чем в другом, тоже бесконечном? Ведь про два бесконечных множества мы можем пока только сказать, эквивалентны они или нет. А существуют ли вообще неэквивалентные бесконечные множества?
Приведём забавную фантастическую историю из книги Н. Я. Виленкина «Рассказы о множествах». Действие происходит в далёком будущем, когда жители разных галактик могут встречаться друг с другом. Поэтому для всех путешествующих по космосу построена огромная гостиница, протянувшаяся через несколько галактик.
В этой гостинице бесконечно много номеров (комнат), но, как и положено, все комнаты пронумерованы, и для любого Натурального числа n есть комната с этим номером.
Однажды в этой гостинице проходил съезд космозоологов, в котором участвовали представители всех галактик. Так как галактик тоже бесконечное множество, все места в гостинице оказались занятыми. Но в это время к директору гостиницы приехал его друг и попросил поселить его в эту гостиницу.
«После некоторых размышлений директор обратился к администратору и сказал:
– Куда же я дену жильца этого номера? – удивлённо спросил администратор.
– А его переселите в № 2. Жильца же из № 2 отправьте в № 3, из № 3 – в № 4 и т. д.»
Вообще, пусть постоялец, живущий в номере K, переедет в номер K+1, как это показано на следующем рисунке:
Тогда у каждого снова будет свой номер, а № 1 освободится.
Таким образом, нового гостя удалось поселить – именно потому, что номеров в гостинице бесконечно много.
Первоначально участники съезда занимали все номера гостиницы, следовательно, между множеством космозоологов и множеством N Было установлено взаимно однозначное соответствие: каждому космозоологу дали по номеру, на двери которого написано соответствующее ему натуральное число. Естественно считать, что делегатов было «столько же», сколько имеется натуральных чисел. Но приехал ещё один человек, его тоже поселили, и количество проживающих увеличилось на 1. Но их снова осталось «столько же», сколько и натуральных чисел: ведь все поместились в гостиницу!
Мы пришли к удивительному выводу: если к множеству, которое равномощно N, добавить ещё один элемент, получится множество, которое снова равномощно N. Но ведь совершенно ясно, что делегаты-космозоологи представляют собой часть того множества людей, которые разместились в гостинице после приезда нового гостя. Значит, в этом случае часть не «меньше» целого, а «равна» целому!
Итак, из определения эквивалентности (которое не приводит ни к каким странностям в случае конечных множеств) следует, что часть бесконечного множества может быть эквивалентна всему множеству.
Новый постоялец не удивился, когда на другое утро ему предложили переселиться в № 1000000. Просто в гостиницу прибыли запоздавшие космозоологи из галактики ВСК-3472, и надо было разместить ещё 999999 жильцов.
Эта задача оказалась весьма сложной. Но и в этом случае нашёлся выход.
«В первую очередь администратор приказал переселить жильца из № 1 в № 2.
– А жильца из № 2 переселите в № 4, из № 3 – в № 6, вообще, из номера N – в номер 2n.
Определение. Множество А, равномощное множеству натуральных чисел N, называется Счетным множеством (имеет мощность счетного множества). Если множество В является бесконечным и не равномощно множеству N, то его называют несчетным.
Множество, которое является конечным или счетным, еще называют не более чем счетным .
Пусть множество А является счетным. По определению, тогда существует биекция А на N, т. е. каждому аÎА соответствует единственный номер nÎN и множество А обращается в некоторую последовательность <аn>.
Теорема 1. Любое подмножество счетного множества не более чем счетно.
Доказательство. Пусть А = 

Теорема 2. Объединение конечного или счетного числа счетных множеств является счетным множеством.
Теорема 3. Любое бесконечное множество содержит счетное подмножество.
Доказательство. Выберем в заданном множестве А какой-либо элемент, придав ему единичный индекс: а1. Среди всех оставшихся элементов множества А найдется не равный а1 элемент (в силу бесконечности А). Его мы обозначим через а2. Продолжая этот процесс до бесконечности мы получим необходимое нам счетное множество
Доказательство. Пусть множество М – А не более чем счетно. Тогда множество М = АÈ(М – А) по теореме 2 не более чем счетно. Это противоречит тому, что множество М несчетно и, следовательно, наше исходное предположение не верно. Таким образом, множество М – А несчетно. Последнее еще не означает равномощности множеств М и М – А. Докажем ее. Выделим из М – А счетное множество В. Обозначим через С множество С = (М – А) – В. Справедливы равенства М = АÈВÈС и М – А = ВÈС. Множество АÈВ счетно (теорема 2). Следовательно, существует биекция f из АÈВ на А. Теперь можно построить биекцию g из М на М – А по правилу:
Теорема 5. Если множество С бесконечно, а В не более чем счетно, то множество ВÈС равномощно множеству С.
Доказательство. Если множество С счетно, то множество ВÈС также счетно и следовательно они равномощны. Если же множество С не счетно, то мы можем воспользоваться теоремой 4, положив в ней А = СÇВ, а М = С.
Теорема 6. Если множество С является бесконечным, то существует его подмножество В такое, что В¹С и В равномощно с С.
Доказательство. По теореме 3 мы можем выделить из множества С его счетное подмножество А. Если множество С счетно, то в качестве В из утверждения теоремы можно взять В=А. Если же С не счетно, то можно положить В=С-А и утверждаемое вытекает из теоремы 4.
Теорема 7. Множество рациональных чисел Q является счетным.
Доказательство. Обозначим через Р множество всех пар натуральных чисел (p, q), таких что p и q не имеют общих целых делителей, кроме единицы. Для пары натуральных чисел (p, q) введем ее высоту m = p + q. Обозначим Рn множество пар натуральных чисел высоты n. Нетрудно проверить, что каждое множество Рn является конечным и содержит не более, чем n-1 член. Так как Р = Èn Рn, то множество Р счетно в силу теоремы 2.
Теорема 8. Множество точек интервала (0,1) является несчетным.
Доказательство (Диагональный метод Кантора). Доказательство проведем от противного, предположив, что множество точек интервала (0,1) является счетным. Тогда все точки можно записать в виде последовательности:
Множества, равномощные множеству точек интервала (0, 1), называются множествами мощности Континуум .
Задачи.
1. Показать, что если множества А и В являются счетными, то и их произведение А´В является счетным.
2. Установить биекцию между множеством N всех натуральных чисел и множеством Q всех четных положительных чисел.
3. Установить биекцию между множеством N всех натуральных чисел и множеством Р всех четных чисел.
Как вообразить несчетное множество?
Как известно, бесконечности бывают разных типов. Бывают счетные, бывают несчетные. Несчетные делятся на множества мощности континуум и все остальные. Счетные множества это такие, элементы которых можно упорядочить в длинный ряд и занумеровать натуральными числами. С несчетными такой фокус не удается. Тогда как же можно представить несчетное множество, в частности множество вещественных чисел [0;1)? Ответ — дерево бесконечной высоты.
Для меня несчетные множества всегда выглядели как непонятное, туманное облако символов витающее где-то на задворках мозга. Но вот недавно
облако скондесировалось в пару не слишком аккуратных, но компактных кристаллов. О них собственно и речь.
Чтобы избежать путаницы, под несчетным множеством будем подразумевать множество мощности континуум (к таким относятся вещественные числа, иррациональные числа, множество всех подмножеств натуральных чисел и другие).
Карусель
Как известно из википедии и других достоверных источников, мощность вещественных чисел отрезка [0;1) является континуумом. Вещественные числа из этого отрезка нельзя посчитать натуральными числами, т.е. сделать так чтобы одному натуральному числу соответствовало одно вещественное и наоборот. Для неверующих проведем диагональную процедуру Кантора.
Представим чисела отрезка [0,1) в двоичной системе счисления и получим набор бесконечных последовательностей единиц и нулей. 
Допустим, мы упорядочили такой набор в виде бесконечного списка как на рисунке. Упорядочив, получим квадратную таблицу в каждой ячейке которой находится либо 1, либо 0. Рассмотрим ячейки располагающиеса на главной диагонали. 
Инвертировав диагональ(000010. ) получим последовательность не попадающую в наш список, так как полученная последовательнось отличается от каждой попавшей в список хотя бы одним элементом. Последовательность номер n будет отличаться от диагональной в n-ой позиции. Следовательно, диагональная последовательность отсутствует в списке.
Исходя из приведенной схемы несчетное множество можно представлять в виде непрерывногенерируемых последовательностей. Инвертировали одну диагональную последовательность — вставили её в начало списка — сгенерировали новую и так далее. Такая карусель выглядит сомнительно.
Дерево
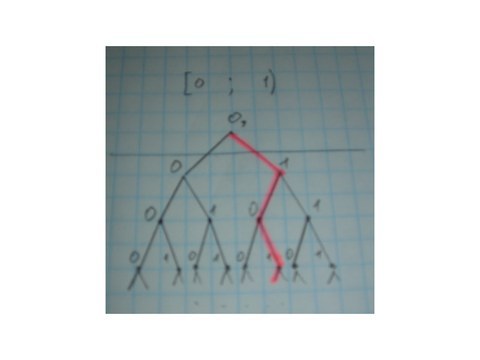
Получается, множество максимальных путей в бинарном дереве бесконечной высоты имеет мощность континуум, что эквивалентно мощности вещественных чисел отрезка [0;1).
Если вернуться к интерпретации бинарных последовательностей как двоичных дробей, то рациональные дроби вида 0,x(y) будут выглядеть в виде конечной кривулины х и бесконечной последовательности кривулин y, иррациональные числа будут выглядеть как одна бесконечная неповторяющаяся кривулина x.
Смешная загогулина
В полученном результате есть одна загвоздка: Количество путей максимальной длинны, исходящих из корня двоичного дерева бесконечной высоты несчетно. Количество же вершин такого дерева можно посчитать. Это легко сделать последовательно нумеруя вершины сверху вниз.
Для дерева конечной высоты расклад другой:
Количество путей максимальной длинны, исходящих из корня в двоичном дереве высотой N равно 2^(N-1), а количество вершин почти в два раза больше — 2^N — 1. Устремляя N к бесконечности получим, что счетная бесконечность вершин в два раза “больше” несчетной бесконечности путей.
Вот такой псевдопарадокс, иллюстрирующий работу интуиции.
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Теорема о континууме
* Если подмножеств конечно, то обозначим множества 


* Если же их счётно, то наибольшего может не существовать. Но если между счётным и континуальным нет мощности (континуум-гипотеза), то это всё равно верно, доказательство аналогично первому пункту. Поэтому если можно доказать, что факт неверен, то найдётся промежуточная, а потому доказуемо опровержение континуум-гипотезы. Но из аксиоматики ZFC это сделать невозможно. Однако из недоказуемости обратного не следует верность данного утверждения, или я что-то путаю?
Также я нашёл в брошюрке, на стр. 25-26, этот факт и более общее утверждение, что множество всех подмножеств 


| Заслуженный участник |
| Заморожен |
Последний раз редактировалось Профессор Снэйп 19.09.2012, 22:10, всего редактировалось 2 раз(а).
А если объединяем счётное число несчётных, но менее чем континуальных?
Или Вы континуум-гипотезу привлечь хотите? Так вроде без неё доказать надо!
Ну а диагональ построить нельзя?
Вот есть у нас семейство 



А вот тут как раз всё просто. Докажите следующую лемму:
Если 



Из неё сразу следует нужное Вам утверждение. А лемму легко доказать, опираясь на 
| Заслуженный участник |
Последний раз редактировалось CptPwnage 20.09.2012, 00:31, всего редактировалось 2 раз(а).
| Заслуженный участник |
| Заморожен |
А пока суть да дело, спал да принимал душ, Padawan уже всё расписал!
| Заслуженный участник |

Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей