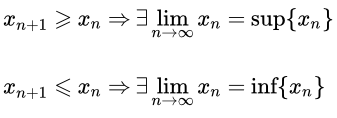Как доказать что последовательность монотонна

Предел монотонной последовательности

Монотонная последовательность. Точные грани последовательности.

Последовательность \(\\>\) называют возрастающей (неубывающей), если для любого \(n\in\mathbb\) выполняется неравенство
$$
x_\geq x_.\label
$$
Аналогично последовательность\(\\>\) называют убывающей (невозрастающей), если для любого \(n\in\mathbb\) справедливо неравенство
$$
x_\leq x_.\label
$$
Если неравенство \eqref можно записать в виде \(x_>x_\), а неравенство \eqref — в виде \(x_ 0 \ \exists x_<\varepsilon>\in X:x_<\varepsilon>>M-\varepsilon\>.\label
$$
Аналогично определение точной нижней грани \(\displaystyle \inf\) числового множества \(X\) можно записать в виде
$$
\displaystyle \\Leftrightarrow\<\forall x\in X\rightarrow x\geq m\>\wedge\<\forall\varepsilon>0\ \exists x_<\varepsilon>\in X:x_ <\varepsilon>0\ \exists N_<\varepsilon>:x_>>a-\varepsilon\>,\label
$$
$$
[b=\displaystyle \inf\\>]\Leftrightarrow\<\forall n\in N\rightarrow x_\geq b\>\wedge\<\forall\varepsilon 0\) (рис. 6.1) найдется член последовательности, больший \(a-\varepsilon\), то есть
$$
\forall\varepsilon>0 \ \exists N_<\varepsilon>:x_>>a-\varepsilon.\label
$$

Рис. 6.1

Аналогично разъясняется определение \eqref точной нижней грани последовательности.

Признак сходимости монотонной последовательности.

Если последовательность \(\<>\>\) является возрастающей и ограниченной сверху, то существует
$$
\lim_x_=\sup\\>.\nonumber
$$

Если последовательность \(\\>\) является убывающей и ограниченной снизу, то существует
$$
\lim_x_=\inf\\>.\nonumber
$$

\(\circ\) Ограничимся доказательством теоремы для случая ограниченной сверху и возрастающей последовательности.

Если последовательность \(\\>\) ограничена сверху, то есть множество чисел \(x_<2>,x_<2>, \ldots,x_, \ldots\) ограничено сверху, то по теореме о существовании верхней грани существует точная верхняя грань этой последовательности, определяемая условиями \eqref, \eqref. Так как \(\\>\) — возрастающая последовательность, то
$$
\forall n\geq N_<\varepsilon>\rightarrow x_>\leq x_.\label
$$

Из \eqref-\eqref следует, что
$$
\forall\varepsilon>0 \ \exists N_<\varepsilon>:\forall n\geq N_<\varepsilon>\rightarrow a-\varepsilon Замечание 1.

Теорема 1 остается справедливой для последовательности, ограниченной сверху (снизу) и возрастающей (убывающей), начиная с некоторого номера.

Источник

Математический портал

Nav view search

Navigation

Search

Последовательность. Ограниченность и монотонность последовательности. Предел последовательности.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Критерий Коши.

Принцип Больцано-Вейерштрасса.

Всякая ограниченная последовательность имеет хотя бы одну предельную точку.

Примеры.

В задачах 1.213, 1.215 написать первые пять членов последовательности:

Решение.

Решение.

Решение.

Из условия запишем:

Продолжая данный ряд, находим общий член последовательности:

Решение.

Из условия запишем:

Решение.

Из условия запишем:

Решение.

Решение.

Запишем несколько первых членов последовательности:

1.229. Используя логическую символику записать следующие высказывания, а так же их отрицания:

а) последовательность ограничена;

Решение.

$$\exists A>0;\,\,\, \forall n\in N (|x_n|\leq A).$$

$$\forall A>0;\,\,\, \exists n\in N (|x_n|>A).$$

б) последовательность монотонно возрастает;

Последовательность монотонно возрастает:

$$\exists n\in N (x_n\geq x_).$$

$$\forall\varepsilon>0 \exists n\in N (|x_n-a|

$$\exists\varepsilon>0 \forall n\in N (|x_n-a|\geq \varepsilon).$$

Источник

Теорема Вейерштрасса о пределе монотонной последовательности

Теорема Вейерштрасса о пределе монотонной последовательности

Любая монотонная ограниченная последовательность < x_n > имеет конечный предел, равный точной верней границе, sup < x_n > для неубывающей и точной нижней границе, inf < x_n > для невозрастающей последовательности.
Любая монотонная неограниченная последовательность имеет бесконечный предел, равный плюс бесконечности, для неубывающей и минус бесконечности, для невозрастающей последовательности.

Доказательство

1) Пусть последовательность является неубывающей ограниченной последовательностью.

Поскольку последовательность ограничена, то она имеет конечную точную верхнюю границу
.
Это означает, что:

Поскольку последовательность ограничена, то она имеет конечную точную нижнюю границу
.
Это означает следующее:

Теперь рассмотрим неограниченные последовательности.
3) Пусть последовательность является неограниченной неубывающей последовательностью.

Поскольку последовательность неубывающая, то при имеем:
.
Здесь мы также использовали (3.2).

4) Наконец рассмотрим случай, когда является неограниченной невозрастающей последовательностью.

Поскольку последовательность невозрастающая, то при имеем:
.

Пример решения задачи

Представим последовательность в виде рекуррентных формул:
,
.

Поскольку последовательность возрастает и ограничена сверху, то она является ограниченной последовательностью. Поэтому, по теореме Вейерштрасса, она имеет предел.

Источник

Числовая последовательность

Определение 1. Числовой последовательностью называется функция, аргументом которой является множество всех натуральных чисел, или множество первых n натуральных чисел.

Обозначается числовая последовательность так:

где −i-ый член последовательности.

При словестном задании последовательности, описывается из каких элементов она состоит.

Последовательность нечетных чисел:

Последовательность простых чисел :

Последовательности (1) и (2) мы задали словестно.

Последовательность нечетных чисел аналитически задается формулой

Отметим, что последовательность простых чисел невозможно задать аналитически.

Пример задания рекуррентной последовательности:

В этой последовательности

Пример стационарной последовательности:

Возрастающие и убывающие последовательности

Определение 3. Последовательность, в которой каждый последующий член (кроме первого) больше предыдующего, называется возрастающей :

Определение 4. Последовательность, в которой каждый последующий член (кроме первого) меньше предыдующего, называется убывающей :

Пример 1. Выяснить, монотонна ли последовательность

Решение. Запишем n+1 член последовательности (подставим вместо n, n+1):

Найдем разность членов и :

.

(3)

Так как n=1,2,3. то правая часть уравнения (3) положительна. Тогда:

Таким образом, каждый последующий член последовательности больше предыдующего. Следовательно последовательность является возрастающим (и монотонным).

Пример 2. Выяснить, при каких значениях a последовательность (b_n) является возрастающей и при каких, убывающей:

Решение. Запишем n+1 член последовательности (вместо n подставим n+1):

Найдем разность членов и :

(4)

Посмотрим на правую часть выражения (4). Если a 10, то . Тогда последовательность является убывающей. При a=10 . Последовательность имеет одинаковые члены:

т.е. имеем дело с последовательностью

Очевидно, что последовательность (5) не является монотонной. Она является стационарной последовательностью.

Ограниченные и неограниченные последовательности

Определение 5. Последовательность (y_n) называется ограниченной сверху, если существует такое число k, что y_n Определение 6. Последовательность (y_n) называется ограниченной снизу, если существует такое число k, что y_n>k при любом n.

Определение 7. Последовательность (y_n) называется ограниченной, если она ограничена и сверху, и снизу.

Пример 3. Показать, что последовательность (a_n) является монотоннной и ограниченной:

Решение. Запишем n+1 член последовательности (вместо n подставим n+1):

Найдем разность членов и :

(6)

Правая часть равенства (6) положительна при любых натуральных чисел n. Следовательно последовательно (a_n) возрастающая (и монотонная).

Далее, сделаем эквивалентное преобразование для проследовательности (5):

Из выражения (7) видно, что при любых n a_n≤1. Т.е. хотя последовательность возрастает, то остается меньше числа 1 (ограничена сверху). Запишем несколько членов данной последовательности, задав n=1,2,3.

Так как последовательность возрастающая, то все члены последовательности не меньше . Тогда последовательность ограничена также и снизу. Таким образом последовательность ограничена и всерху, и снизу, т.е. является ограниченной последовательностью.

Сходящиеся и расходящиеся последовательности

Рассмотрим две числовые последовательности:

На координатной прямой изобразим члены этих последовательностей:

Предел числовой последовательности

Точка, к которой приближаются члены последовательности при увеличении n, называется пределом последовательности. Для последовательности (10) пределом является число 0. Более строго предел последовательности определяется так:

Определение 8. Число k называют пределом последовательности (y_n), если для любой заранее выбранной окресности точки k, можно выбрать такой номер n₀, чтобы все члены последовательности, начиная с номера n₀ содержались в указанной окрестности.

Если k является пределом последовательности (y_n), то пишут ( стремится к k или сходится к k).

Обозначают это так:

Выраженние (11) читается так: предел проследовательности , при стремлении n к бесконечности равен k.

Изложим некоторые пояснения к определению 8.

Пусть выполнено (11). Возьмем окрестность точки k, т.е. интервал , где радиус этой окрестности ( >0). По определению, существует номер n₀, начиная с которого вся последовательность содержится в указанной окресности, т.е.

.

Если же взять другую окресность (пусть ), то найдется другой номер n₁, начиная с которого, вся последовательность содержится в указанной окрестности, но этот номер будет больше n₁ > n₀.

Пример 4. Дана полследовательность (y_n):

Доказать, что .

Решение. Найдем любую окрестность точки 0. Пусть ее радиус равен r. Тогда всегда можно выбирать n₀ так, чтобы .

Пусть, например, r=0.001. Вычислим n‘ из уравнения

.

В качестве n₀ берем 501. Имеем:

.

Запишем члены последовательности (12) начиная с номера 501:

.

Далее, учитывая (13), имеем:

.

Следовательно, все члены последовательности (12) начиная с номера 501 попадают в окресность . А по определению 8, это означает:

Пример 5. Дана полследовательность (y_n):

Доказать, что .

Решение. Найдем любую окрестность точки 2. Пусть ее радиус равен r. Тогда всегда можно выбирать n₀ так, чтобы

.

.

Неравенство в (17) всегда выполняется так как n₀ натуральное число, а правая часть неравенства отрицательно (это означает, что для любого n₀). Из неравенства (16) можно найти номер n₀, начиная с которого члены последовательности попадают в окресность (2−r; 2+r). Например, пусть r=0.001, тогда . Тогда нужно брать n₀=2000. И тогда все члены последовательности, начиная с номера 2000 попадают в окрестность (2−r; 2+r).

Запишем члены последовательности, начиная с номера 2000:

.

Легко проверить, что . Тогда, учитывая, что данная последовательность возрастающая (см. пример 1), получим:

.

Пример 6. Найти предел последовательности

Решение. Выполним некоторые преобразования выражения (18):

Тогда последовательность (18) можно переписать так:

(19)

Как видно из (19), пройдя по членам последовательности слева направо, из числа 1 вычитается все меньшее и меньшее положительное число. Т.е. последовательность приближается к числу 1. Тогда 1 является пределом последовательности (19) и (18):

Свойства сходящихся последовательностей

Сходящиеся последовательности обладают рядом свойств.

Свойство 1. Если последовательность сходится, то только к одному пределу.

Свойство 2. Если последовательность сходится, то она ограничена.

Свойство 3. Если последовательность монотонна и ограничена, то она сходится (теорема Вейерштрасса).

Предел стационарной последовательности равен значению любого члена последовательности:.

Теорема. Если , то

1. Предел суммы равен сумме пределов:

2. Предел произведения равен произведению пределов:

3. Предел частного равен частному пределов:

4. Постоянный множитель можно вывести за знак предела:

Пример 7. Найти предел последовательности:

Решение. Так как , то

.

Пример 8. Найти предел последовательности:

Решение. Применив правило «предел суммы» теоремы, получим

.

Пример 9. Вычислить:

Решение. Делим числитель и знаменатель дроби на наивысшую из имеющихся степень переменного n. Далее используем правило «предел суммы» для числителя и знаменателя и правило «предел частного»:

Источник