Как доказать что три точки лежат на одной прямой

Как доказать что три точки лежат на одной прямой

Если три точки A, B и C лежат на одной прямой, то треугольник ABC обратится в отрезок прямой, а потому его площадь должна быть равна нулю. Полагая в формуле

S = 0, получим условие, при котором три точки лежат на одной прямой

В более удобной форме условие, при котором три точки лежат на одной прямой, можно записать так:

(1)

Подставляя сюда координаты данных точек, получим, что левая часть (1) будет равна

Требование (1) выполнено:

и, значит, три данные точки лежат на одной прямой.

Источник

Когда 3 точки лежат на одной прямой

Очень часто при решения домашней работы возникает вопрос: когда 3 точки лежат на одной прямой, ответ очень прост и он лежит в основе геометрии.

Осуществить проверку того, что три точки лежат на одной прямой можно через составления уравнения, рассматриваемой прямой, которая проходит через две наугад выбранные точки из этих трех. И проверки того, что этому уравнению удовлетворяют координаты оставшейся из этих трех точек.

Есть разные виды уравнения прямой. Воспользуемся одним из простейших способов и рассмотрим его для конкретно заданных точек.

Это сделаем лишь для того, чтобы не решать поставленную задачу в общем виде, а чтобы дать ответ на вопрос лежат ли 3 именно эти точки с этими координатами на одной прямой. Сформулируем задачу: Необходимо проверить лежат ли точки A(-2;1), Б(0;3), В (5;-7) на одной прямой.

Решим поставленную задачу

Как известно, через любые две точки можно провести прямую, причем единственную. Вот и проведем мысленно эту прямую. Допустим, прямую АБ. Значит, решение нашей задачи свелось к тому, что нужно проверить: принадлежит ли точка В прямой АБ. Если окажется, что точка В принадлежит прямой АБ, то все точки из условия будут лежать на одной прямой. Если мы выясним, что точка В не принадлежит прямой АБ, то можно будет утверждать, что точки А, Б и В на одной прямой не лежат. Составим уравнение прямой АБ как уравнение прямой проходящей через две точки:

После преобразования получим:

Как видим, не получили верное числовое равенство. Значит в этом случае точки А, Б, В не лежат на одной прямой.

Пример, когда 3 точки лежат на одной прямой можно легко подобрать для этой задачи. Всего лишь точка В должна иметь координаты (0;3) или (-7;-4)

Источник

Теорема Менелая, теорема Чевы – нужны на ЕГЭ или нет?

Разберемся, что это за теоремы и как применяются. И действительно ли на ЕГЭ дали задачи на применение теорем, выходящих за рамки школьной программы. И можно ли эти задачи решить по-другому?

Теорема Менелая:

Пусть прямая пересекает произвольный треугольник причем – точка ее пересечения со стороной – точка ее пересечения со стороной и – точка ее пересечения с продолжением стороны

Тогда выполняется равенство:

Как это запомнить? Сначала рисуем треугольник Затем прямую, пересекающую две его стороны и продолжение третьей. На этой прямой лежат точки и причем на стороне должна лежать точка на стороне – точка и на продолжении – точка

Затем записываем равенство так, как будто «обходим» весь треугольник от точки к точкам и и затем возвращаемся в точку Но по дороге нам встречаются точки и – их тоже включаем в формулу.

В некоторых задачах полезна обратная теорема Менелая.

Теорема (Менелая, обратная). Пусть дан треугольник Предположим, что точка лежит на стороне точка лежит на стороне а точка лежит на продолжении стороны причём про эти точки известно, что

Тогда эти точки лежат на одной прямой.

Как правило, не так-то просто бывает доказать, что три точки лежат на одной прямой. Обычно мы используем для доказательства такого факта косвенные методы. Например, если для точек и выполняется равенство: – то это означает, что точка лежит на отрезке Или, если нам удается доказать, что угол – развернутый, это и будет означать, что точки и лежат на одной прямой. Обратная теорема Менелая дает еще один способ доказательства того, что три точки – в данном случае и – лежат на одной прямой.

Теорема Чевы

Пусть точки и лежат соответственно на сторонах и треугольника причем отрезки и пересекаются в одной точке. В этом случае выполняется равенство:

Обратная теорема Чевы:

Теорема (Чевы, обратная). Пусть точки лежат соответственно на сторонах и треугольника причём

Тогда отрезки и пересекаются в одной точке.

Как применяются теоремы Менелая и Чевы?

Вот задача Профильного ЕГЭ по математике 2020 года (№16), Санкт-Петербургский вариант.

На сторонах и треугольника отмечены точки и соответственно, причём Отрезки и пересекаются в точке

а) Докажите, что — параллелограмм.
б) Найдите если отрезки и перпендикулярны,

Докажем пункт (а) с помощью теоремы Менелая:

Это значит, что по двум углам и то есть

Прямая пересекает две его стороны и продолжение третьей стороны

По теореме Менелая,

по углу и двум сторонам, отсюда

— параллелограмм по определению.

Мы доказали то, что требовалось в пункте (а).
Но что делать, если теоремы Менелая и Чевы вы не проходили в школе? Ничего страшного, докажем без теорем Менелая и Чевы. Их легко заменят подобные треугольники.

Докажем, что — параллелограмм.

Тогда по углу и двум пропорциональным сторонам,

Это значит, что по углу и двум сторонам и

Получим, что в четырёхугольнике :

Как видим, эти решения примерно одного уровня сложности.
А вот в пункте (б) нет необходимости применять теоремы Чевы и Менелая. Он легко решается с помощью обычной школьной геометрии.

Поскольку получим, что — прямоугольный.

Мы доказали в пункте (а), что — трапеция, причём

Тогда — параллелограмм (по признаку паралелограмма)

по теореме Пифагора из

Найдём из по теореме косинусов.

Вот еще одна задача, которую можно решить как с помощью теоремы Чевы, так и без нее.

На сторонах прямоугольного треугольника с прямым углом построены во внешнюю сторону квадраты и Докажите, что:

а) прямые и отсекают от катетов треугольника равные отрезки
б) прямые и высота треугольника проведённая из вершины пересекаются в одной точке.

Пункт (а) доказывается легко.

Решим пункт (б) с помощью теоремы Чевы:

Запишем, чему равны длины отрезков Для длин и воспользуемся тем, что в прямоугольном треугольнике каждый катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

Проверим выполнение равенства

Равенство выполняется.
Согласно теореме Чевы, это значит, что и пересекаются в одной точке.
А вот как решается эта задача без теоремы Чевы, с помощью векторов:

Математик Менелай Александрийский жил в I веке до нашей эры (Древний Рим).
Математик и инженер Джованни Чева – XVII век, Италия.

Как видим, теоремы Менелая и Чевы оказываются полезны в некоторых задачах. Очень хорошо, если вы знаете эти теоремы. Однако если они для вас непривычны, можно применить простой школьный прием – пары подобных треугольников.

Это полезно

В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.

Источник

Высшая математика. Шпаргалка

Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.

Оглавление

Приведённый ознакомительный фрагмент книги Высшая математика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.

2. Условие нахождения трех точек на одной прямой. Уравнение прямой. Взаимное расположение точек и прямой. Пучок прямых. Расстояние от точки до прямой

3. Пусть имеются точка М (х₁, у₁) и некоторая прямая L, представленная уравнением у = ах + с. Уравнение прямой, проходящей параллельно данной прямой L через данную точку М:

Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М, описывается уравнением А(х — х₁) + В(у — у₁) = 0.

Уравнение прямой, проходящей перпендикулярно данной прямой L через данную точку М:

Если прямая L задана уравнением Ах + Ву + С = 0, то параллельная ей прямая, проходящая через точку М(х₁, у₁), описывается уравнением А (у — у₁) — В(х — х₁) = 0.

4. Пусть даны две точки А₁ (х₁, у₁), А₂ (х₂, у₂) и прямая, заданная уравнением Ах + Ву + С = 0. Взаимное расположение точек относительно этой прямой:

1) точки А₁, А₂ лежат по одну сторону от данной прямой, если выражения (Ах₁ + Ву₁ + С) и (Ах₂ + Ву₂ + С) имеют одинаковые знаки;

3) одна или обе точки А₁, А₂ лежат на данной прямой, если одно или оба выражения соответственно (Ах₁ + + Ву₁ + С) и (Ах₂ + Ву₂ + С) принимают нулевое значение.

5. Центральный пучок — это множество прямых, проходящих через одну точку М (х₁, у₁), называемую центром пучка. Каждая из прямых пучка описывается уравнением пучка у — у₁ = к (х — х₁) (параметр пучка к для каждой прямой свой).

Все прямые пучка можно представить уравнением: l(y — y₁) = m(x — x₁), где l, m — не равные одновременно нулю произвольные числа.

6. Пусть даны точка М (х₁, у₁) и прямая, заданная уравнением Ах + Ву + С = 0. Расстояние d от этой точки М до прямой:

Источник

Через три точки можно провести плоскость

Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика:Существование плоскости, проходящей через три данные точки

Существование плоскости, проходящей через три данные точки

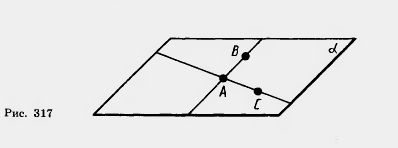
Теорема 15.3. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

Доказательство. Пусть А, В, С — три данные точки, не лежащие на одной прямой (рис. 317). Проведем прямые АВ и АС; они различны, так как точки А, В, С не лежат на одной прямой. По аксиоме Сз через прямые АВ и АС можно провести плоскость . Эта плоскость содержит точки А, В, С.

Докажем, что плоскость а, проходящая через точки А, В, С, единственна. Действительно, плоскость, проходящая через точки А, В, С, по теореме 15.2 содержит прямые АВ и АС. А по аксиоме Сз такая плоскость единственна.

Задача (13). Можно ли провести плоскость через три точки, если они лежат на одной прямой? Объясните ответ.

Решение. Пусть А, В, С — три точки, лежащие на прямой . Возьмем точку D, не лежащую на прямой (аксиома I). Через точки А, В, D можно провести плоскость (теорема 15.3). Эта плоскость содержит две точки прямой — точки A и В, а значит, содержит и точку С этой прямой (теорема 15.2).

Следовательно, через три точки, лежащие на одной прямой, всегда можно провести плоскость.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.

сколько плоскостей можно провести через

две различные точки

три различные точки

четыре точки никакие три из которых не лежат на одной прямой.

В рамках этого материала мы разберем, как найти уравнение плоскости, если мы знаем координаты трех различных ее точек, которые не лежат на одной прямой. Для этого нам понадобится вспомнить, что такое прямоугольная система координат в трехмерном пространстве. Для начала мы введем основной принцип данного уравнения и покажем, как именно использовать его при решении конкретных задач.

Как найти уравнение плоскости, которая проходит через 3 заданные точки

Для начала нам необходимо вспомнить одну аксиому, которая звучит следующим образом:

Если три точки не совпадают друг с другом и не лежат на одной прямой, то в трехмерном пространстве через них проходит только одна плоскость.

Иными словами, если у нас есть три разных точки, координаты которых не совпадают и которые нельзя соединить прямой, то мы можем определить плоскость, проходящую через нее.

Зная координаты нормального вектора и координаты точки, через которую проходит плоскость, мы можем записать общее уравнение этой плоскости.

Из этого мы и будем исходить в дальнейшем.

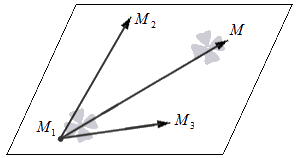
n → = M 1 M 2 → × M 1 M 3 → = i → j → k → x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1

На схеме это будет выглядеть так:

Запишем полученное уравнение в координатной форме:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0

От полученного в результате уравнения можно перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости, если этого требуют условия задачи.

В следующем пункте мы приведем примеры того, как указанные нами подходы реализуются на практике.

Примеры задач на составление уравнения плоскости, проходящих через 3 точки

Ранее мы выделили два подхода, с помощью которых можно найти искомое уравнение. Давайте посмотрим, как они применяются в решениях задач и когда следует выбирать каждый из них.

Решение

Используем поочередно оба способа.

Теперь вычислим их векторное произведение. Вычисления определителя расписывать при этом не будем:

n → = M 1 M 2 → × M 1 M 3 → = i → j → k → 2 0 5 6 1 0 = – 5 · i → + 30 · j → + 2 · k →

Это и есть нужное нам уравнение плоскости, которая проходит через три точки.

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = x – ( – 3 ) y – 2 z – ( – 1 ) – 1 – ( – 3 ) 2 – 2 4 – ( – 1 ) 3 – ( – 3 ) 3 – 2 – 1 – ( – 1 ) = = x + 3 y – 2 z + 1 2 0 5 6 1 0 = – 5 x + 30 y + 2 z – 73

Мы получили нужное нам уравнение.

А как быть, если заданные точки все же лежат на одной прямой и нам нужно составить уравнение плоскости для них? Здесь сразу надо сказать, что это условие будет не совсем корректным. Через такие точки может проходить бесконечно много плоскостей, поэтому вычислить один-единственный ответ невозможно. Рассмотрим такую задачу, чтобы доказать некорректность подобной постановки вопроса.

Решение

Векторное произведение будет равно:

M 1 M 2 → × M 1 M 3 → = i → j → k → – 4 6 2 – 6 9 3 = 0 · i ⇀ + 0 · j → + 0 · k → = 0 →

Если мы используем второй способ, у нас получится:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0 ⇔ x – 5 y – ( – 8 ) z – ( – 2 ) 1 – 5 – 2 – ( – 8 ) 0 – ( – 2 ) – 1 – 5 1 – ( – 8 ) 1 – ( – 2 ) = 0 ⇔ ⇔ x – 5 y + 8 z + 2 – 4 6 2 – 6 9 3 = 0 ⇔ 0 ≡ 0

Если вы хотите найти хоть один ответ этой задачи из бесконечного множества ее вариантов, то нужно выполнить следующие шаги:

Источник