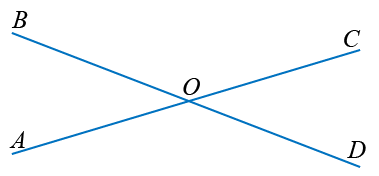
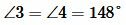Как доказать что вертикальные углы равны
Инструменты пользователя
Инструменты сайта
Боковая панель
Геометрия:
Контакты
Содержание
Смежные и вертикальные углы. Перпендикулярные прямые
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
Теорема 1. Сумма смежных углов равна 180°.
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
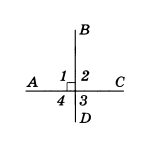
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Отыскание смежных углов треугольника. Пример 5
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°.
Вертикальные углы. Свойства вертикальных углов
Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.
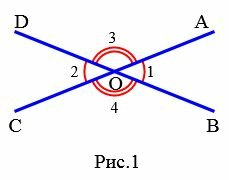 |
На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.
Свойства вертикальных углов
1. Вертикальные углы равны.
2. Две пересекающие прямые образуют две пары вертикальных углов.
Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем
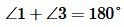 , , 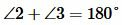 |
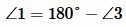 , , 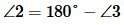 |
Следовательно 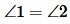
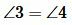
Задачи и решения
Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).
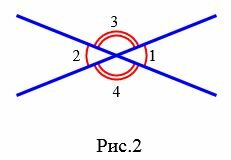 |
Решение. Так как углы 1 и 2 вертикальны, то 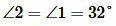
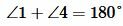
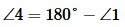 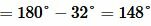 . . |
Углы 3 и 4 вертикальные. Тогда
Ответ. 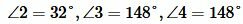
Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.
Ответ. 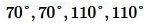
Смежные и вертикальные углы
Смежные углы
Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют развёрнутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны (только в том случае, когда смежные углы не равны).
∠ABD и ∠DBC — это смежные углы, AC — прямая, луч BD — общая сторона углов и наклонная к прямой AC, ∠ABC — развёрнутый угол, B — основание наклонной.
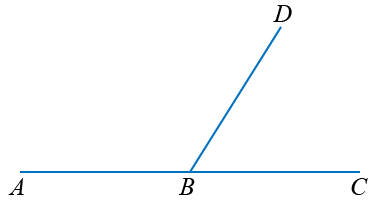
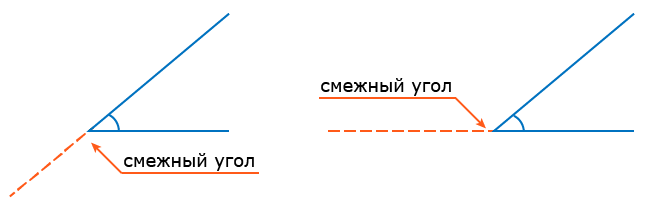
Чтобы построить угол, смежный с данным углом, нужно одну из сторон угла продлить за вершину:
Сумма смежных углов
Любые два смежных угла составляют в сумме развёрнутый угол. Развёрнутый угол равен двум прямым углам, поэтому можно сказать, что сумма двух смежных углов равна двум прямым углам.
где d — это обозначение прямого угла (d = 90°).
Вертикальные углы
Вертикальные углы — это пара углов, у которых стороны одного угла являются продолжением сторон другого угла. Пересечение двух прямых линий образует две пары вертикальных углов:
∠AOB и ∠COD, а также ∠AOD и ∠BOC — вертикальные углы.
Равенство вертикальных углов
Вертикальные углы равны между собой. Рассмотрим вертикальные углы 1 и 3:
Сумма ∠1 и ∠2 равна развёрнутому углу (180°). Сумма ∠2 и ∠3 тоже равна развёрнутому углу (180°). Значит:
Следовательно, ∠1 = ∠3. Равенство вертикальных углов доказано.
Геометрия. 7 класс
Конспект урока
Смежные и вертикальные углы. Аксиомы и теоремы
Перечень вопросов, рассматриваемых в теме:
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
Свойства смежных углов:
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов: вертикальные углы равны.
Аксиома– положение, принимаемое без доказательств.
Теоретический материал для самостоятельного изучения
Давайте построим развёрнутый угол АОС и проведём в нём луч ОВ. В результате у нас получилось два угла ∠АОВ – острый угол и ∠ВОС– тупой угол. Стороны АО и ОС – продолжают друг друга, ВО– общая сторона. Углы АОВ и ВОС – это смежные углы. На основании этого сформулируем определение смежных углов.
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
Давайте докажем это свойство.
Укажем ещё одно свойство смежных углов.
Теперь построим две пересекающиеся прямые, АС и BD. Посмотрите, при пересечении прямых у нас получилось четыре угла: ∠АОВ, ∠АОD, ∠CОD, ∠BОC. Из них попарно являются смежными углы: ∠АОВ и ∠АОD, ∠АОD и ∠CОD, ∠CОD и ∠BОC, ∠АОВ и ∠BОC.
Углы, которые не являются смежными:
∠АОВ и ∠CОD; ∠АОD и ∠BОC. Пары этих углов называются вертикальными углами.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов: вертикальные углы равны. Убедимся в справедливости этого свойства, докажем его.
Доказательство. Посмотрим на чертёж: пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1– смежные углы. Угол 2 одновременно является смежным с углом 1 и с углом 3. По свойству смежных углов
Свойства смежных и вертикальных углов, которые мы сегодня рассмотрели– в геометрии называются теоремами. Правильность утверждения о свойстве той или иной геометрической фигуры устанавливается путём рассуждения. Это рассуждение называется доказательством. А само утверждение, которое доказывается, называется теоремой.
На предыдущих уроках вы познакомились с понятием аксиомы.
В чём же различие между аксиомой и теоремой? Ответ на этот вопрос таков: аксиома – положение, принимаемое без доказательств.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.
Используя чертёж, найдите угол ∠ВОК.
№2. Тип задания: единичный / множественный выбор.
Используя чертёж, найдите угол ∠AOD.
№3. Тип задания: выделение цветом.
Выделите верный ответ из списка:
60 0 ; 30 0 ; 75 0 ; 90 0
Угол. Свойства смежных и вертикальных углов.
Сумма двух смежных углов равна двум прямым углам.
Даны два смежных угла: АОВ и ВОС. Требуется доказать, что:
Восставим из точки О к прямой АС перпендикуляр OD. Мы разделили угол АОВ на две части AOD и DOB так, что можно написать:
Прибавим к обеим частям этого равенства по одному и тому же углу BOС, отчего равенство не нарушится:
что и требовалось доказать.
Следствия.
Если из одной точки ( O) прямой (AB) восстановить к ней, по каждую ее сторону, перпендикуляры, то эти перпендикуляры образуют одну прямую (СD). Из всякой точки вне прямой можно опустить на эту прямую перпендикуляр и притом только один.
Потому, что сумма углов COB и BOD равна 2d.
Прямая С части которой OС и OD служат перпендикулярами к прямой AB, называется прямой перпендикулярной к AB.
Если прямая СD перпендикулярна к прямой AB, то и наоборот: AB перпендикулярна к СD, потому что части OA и OB служат также перпендикулярны к СD. Поэтому прямые AB и СD называются взаимноперпендикулярными.
То, что две прямые AB и СD взаимноперпендикулярны, выражают письменно так AB ^ СD.
Два угла называются вертикальными, если стороны одного составляют продолжение сторон другого.
Два вертикальных угла равны.
Пусть даны два вертикальных угла: AOD и СOB т.е. OB есть продолжение OA, а OС продолжение OD.
По свойству смежных углов можем написать:
Значит: AOD + DOB = DOB + BOС.
Если вычесть из обеих частей этого равенства по углу DOB, получим: