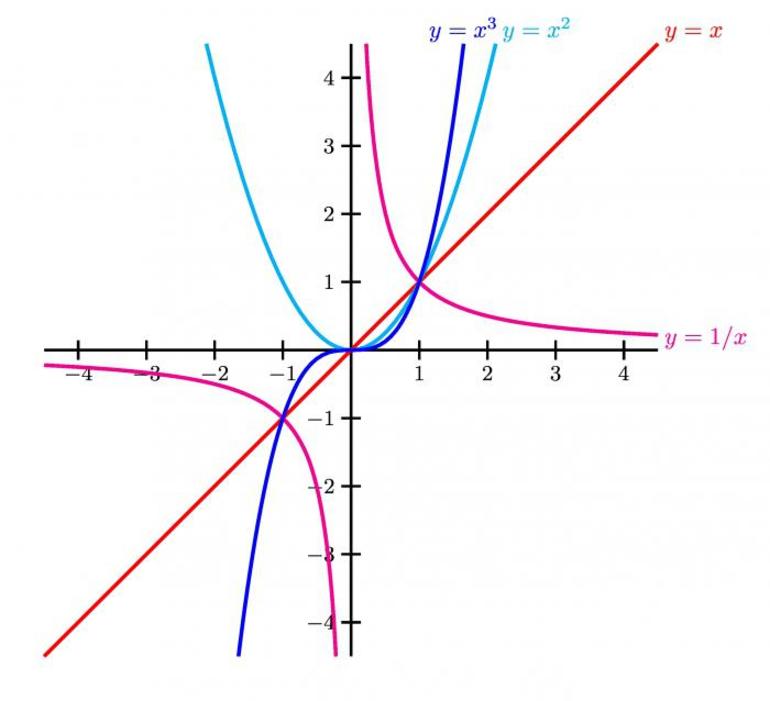
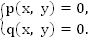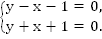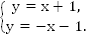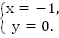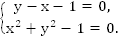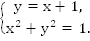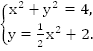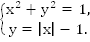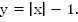Как определить что графики пересекаются
Как найти точки пересечения графиков функций — алгоритмы и примеры правила и методики
Существует определенный класс задач по дисциплине «Алгебра и начало анализа», в которых нужно найти точки пересечения графиков функций без их построения. Решать такие задания довольно просто, когда известна определенная методика нахождения координат по оси абсцисс и ординат. Однако для этого необходимо научиться правильно находить корни уравнений различных типов.
Общие сведения
Функция — некоторое выражение, описывающее зависимость между двумя величинами. Следует отметить, что последних может быть несколько. Параметр, который не зависит от других элементов, называется аргументом, а зависимое тождество — значением функции.
Точка пересечения графиков означает, что у системы уравнений существует общее решение. Следует отметить, что для их нахождения можно воспользоваться графическим и аналитическим методом. Первый подразумевает построение графического представления выражения с переменной.
Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками. Для их нахождения специалисты рекомендуют получить базовые понятия о равенствах с переменными, а также о методах их решения.
Классификация уравнений
Уравнение — тождество, содержащее неизвестные величины (переменные), которые следует найти при помощи определенного алгоритма. Последний зависит от типа выражений. Тождества классифицируются на несколько типов:
Линейными являются уравнения, содержащие единичную степень, т. е. 2t=4. Квадратные — тождества, у которых переменная возведена в квадрат. Они имеют следующий вид: Pt^2+St+U=0, где Р и S — коэффициенты при неизвестных, а U — свободный член.
Кубическое — уравнение вида Ot^3+Pt^2+St+U=0, где O, Р и S — коэффициенты при переменных, а U — константа. Последний вид — равенства, в которых при переменной присутствует четвертая степень (Nt^4+Ot^3+Pt^2+St+U=0).
Равносильные тождества
При выполнении математических операций каждое выражение может быть заменено на эквивалентное, т. е. равносильное. Иными словами, равносильными называются уравнения, различные по составляющим их элементам, но имеющие одинаковые корни. Следует отметить, что ими являются также выражения, не имеющие решений. Математики выделяют три свойства: симметричность, транзитивность и разложение на множители.
Формулировка первого: когда I уравнение равносильно II, то значит, и II равносильно I. Суть транзитивности состоит в том, что если I равносильно II, а II — III, то значит I эквивалентно III. Второе свойство имеет такую формулировку: произведение двух элементов, содержащих переменные, равное нулевому значению, эквивалентно двум выражениям, которые можно приравнять к 0. Математическая запись утверждения имеет такой вид: R(t)*S(t)=0
Математические преобразования
Для решения уравнения необходимо выполнить некоторые математические преобразования. Они должны выполняться грамотно, поскольку любая ошибка приводит к образованию ложных корней. Допустимыми операциями являются следующие:
Специалисты рекомендуют избегать операций, при которых сокращаются неизвестные величины. Следствием этого могут стать ложные корни. Кроме того, делитель не должен иметь значения, при которых его значение равно 0. Последнее условие следует всегда проверять, а при решении ни один корень уравнения не должен соответствовать значению переменной при нахождении окончательных корней.
Однако при решении (t+2)=0 получается, что t=-2, а это недопустимо. Следовательно, вышеописанный метод не всегда подходит.
Разложение на множители
Для решения уравнений при выполнении математических преобразований могут потребоваться специальные формулы разложения на множители. Их еще называют тождествами сокращенного умножения. К ним относятся следующие:
Методики нахождения точек
Чтобы узнать, пересекаются ли графики функций, нужно приравнять соответствующие тождества, а затем решать уравнение. Однако при такой операции могут получиться различные равенства с неизвестными. В этом случае требуется обратить внимание на нижеописанные методики решения для каждого вида.
Первой и второй степени
Уравнение первой степени, или линейное, решается очень просто. Для этого необходимо перенести переменные величины в одну, а известные — в другую сторону. Методика решения имеет следующий вид:
Сложнее решается квадратное уравнение. Существует несколько способов нахождения его корней:
Первый способ применяется довольно часто, поскольку с его помощью можно понижать степень при неизвестной величине. Второй подразумевает выделение квадрата по одной из формул сокращенного умножения. Чтобы воспользоваться одним из двух методов, необходимо знать соответствующие тождества (правила разложения на множители).
Следует отметить, что при Д>0 переменная принимает два значения, которые превращают равенство в истину. Если Д=0, то корень только один. Когда Д Кубические и биквадратные
Решение тождеств кубического и биквадратного типов с неизвестными осуществляется двумя способами. К ним относятся:
В первом случае необходимо выполнить преобразования, которые позволят применить одну из формул сокращенного умножения. Однако этот метод применяется довольно редко, поскольку математики отдают предпочтение второму способу. Для его реализации вводится дополнительная переменная, обладающая более низкой степенью и существенно упрощающая выражение. Алгоритм имеет такой вид:
Для проверки рекомендуется воспользоваться онлайн-приложениями, позволяющими вычислить корни, а также построить графики функций. Кроме того, для кубического многочлена Pt 3 +St 2 +Ut+V=0 существует еще одна методика нахождения корней. Она имеет следующий вид:
Следует отметить, что важным пунктом методики является правильный выбор выражения замены, а затем верное выполнение математических преобразований.
Пример решения
Для закрепления знаний необходимо перейти к практическому решению заданий.Одной из простых задач является следующая: найдите координаты точки пересечения графиков линейных функций z=2t+7 и z=t-1. Решается задача по такому алгоритму:
В четвертом пункте нужно подставить координату по оси абсцисс в любое из уравнений для получения второй составляющей, необходимой для точки. Следует отметить, что в этой задаче нет необходимости проводить математические преобразования. Однако существуют и более сложные задания, в которых необходимо решать квадратные уравнения, а также раскрывать скобки.
Таким образом, для определения точки пересечения графиков необходимо уметь находить корни уравнения, а также выполнять алгебраические преобразования.
Общие сведения
Функция — некоторое выражение, описывающее зависимость между двумя величинами. Следует отметить, что последних может быть несколько. Параметр, который не зависит от других элементов, называется аргументом, а зависимое тождество — значением функции.
Точка пересечения графиков означает, что у системы уравнений существует общее решение. Следует отметить, что для их нахождения можно воспользоваться графическим и аналитическим методом. Первый подразумевает построение графического представления выражения с переменной.
Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками. Для их нахождения специалисты рекомендуют получить базовые понятия о равенствах с переменными, а также о методах их решения.
Классификация уравнений
Уравнение — тождество, содержащее неизвестные величины (переменные), которые следует найти при помощи определенного алгоритма. Последний зависит от типа выражений. Тождества классифицируются на несколько типов:
Равносильные тождества
При выполнении математических операций каждое выражение может быть заменено на эквивалентное, т. е. равносильное. Иными словами, равносильными называются уравнения, различные по составляющим их элементам, но имеющие одинаковые корни. Следует отметить, что ими являются также выражения, не имеющие решений. Математики выделяют три свойства: симметричность, транзитивность и разложение на множители.
Математические преобразования
Для решения уравнения необходимо выполнить некоторые математические преобразования. Они должны выполняться грамотно, поскольку любая ошибка приводит к образованию ложных корней. Допустимыми операциями являются следующие:
Специалисты рекомендуют избегать операций, при которых сокращаются неизвестные величины. Следствием этого могут стать ложные корни. Кроме того, делитель не должен иметь значения, при которых его значение равно 0. Последнее условие следует всегда проверять, а при решении ни один корень уравнения не должен соответствовать значению переменной при нахождении окончательных корней.
Однако при решении (t+2)=0 получается, что t=-2, а это недопустимо. Следовательно, вышеописанный метод не всегда подходит.
Разложение на множители
Для решения уравнений при выполнении математических преобразований могут потребоваться специальные формулы разложения на множители. Их еще называют тождествами сокращенного умножения. К ним относятся следующие:
Методики нахождения точек
Чтобы узнать, пересекаются ли графики функций, нужно приравнять соответствующие тождества, а затем решать уравнение. Однако при такой операции могут получиться различные равенства с неизвестными. В этом случае требуется обратить внимание на нижеописанные методики решения для каждого вида.
Первой и второй степени
Сложнее решается квадратное уравнение. Существует несколько способов нахождения его корней:
Первый способ применяется довольно часто, поскольку с его помощью можно понижать степень при неизвестной величине. Второй подразумевает выделение квадрата по одной из формул сокращенного умножения. Чтобы воспользоваться одним из двух методов, необходимо знать соответствующие тождества (правила разложения на множители).
Следует отметить, что при Д>0 переменная принимает два значения, которые превращают равенство в истину. Если Д=0, то корень только один. Когда Д 3 +St 2 +Ut+V=0 существует еще одна методика нахождения корней. Она имеет следующий вид:
Следует отметить, что важным пунктом методики является правильный выбор выражения замены, а затем верное выполнение математических преобразований.
Пример решения
Для закрепления знаний необходимо перейти к практическому решению заданий.Одной из простых задач является следующая: найдите координаты точки пересечения графиков линейных функций z=2t+7 и z=t-1. Решается задача по такому алгоритму:
В четвертом пункте нужно подставить координату по оси абсцисс в любое из уравнений для получения второй составляющей, необходимой для точки. Следует отметить, что в этой задаче нет необходимости проводить математические преобразования. Однако существуют и более сложные задания, в которых необходимо решать квадратные уравнения, а также раскрывать скобки.
Таким образом, для определения точки пересечения графиков необходимо уметь находить корни уравнения, а также выполнять алгебраические преобразования.
Как найти координаты точек пересечения графика функции: примеры решения
Вы будете перенаправлены на Автор24
В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций.
Первый способ
Второй способ
Второй способ заключается в том, что составляется система из имеющихся уравнений, путём преобразований одну из координат делают явной, то есть, выражают через другую. После это выражение в приведённой форме подставляется в другое.
Решение:
Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:
Подставим наши результаты по оси абсцисс по очереди во второе уравнение системы:
Третий способ
Готовые работы на аналогичную тему
Перейдём к третьему способу — графическому, но имейте в виду, что результат, который он даёт, не является достаточно точным.
Для применения метода оба графика функций строятся в одном масштабе на одном чертеже, и затем выполняется визуальный поиск точки пересечения.
Данный способ хорош лишь в том случае, когда достаточно приблизительного результата, а также если нет каких-либо данных о закономерностях рассматриваемых зависимостей.
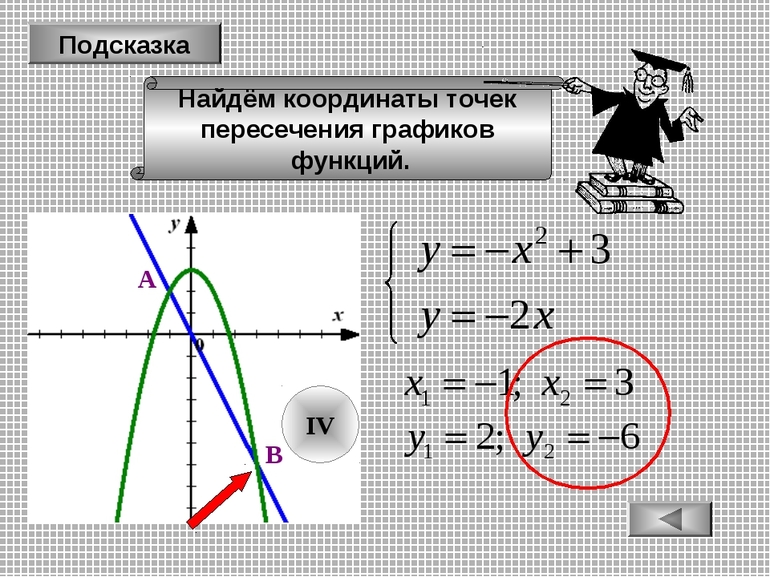
Найдите точку пересечения графиков на общем рисунке.
Рисунок 1. Точка пересечения двух функций. Автор24 — интернет-биржа студенческих работ
Решение:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 07 05 2021
Как решать задачи на квадратичную функцию
В предыдущем уроке мы подробно разобрали, как построить параболу. В этом уроке мы разберем, как решать типовые задачи на квадратичную функцию.
Как найти нули квадратичной функции
Подставим в исходную функцию вместо « y » ноль и решим полученное квадратное уравнение.
0 = x 2 − 3
x 2 − 3 = 0
x1;2 =
| 0 ± √ 0 2 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
| ± √ 12 |
| 2 |
x1;2 =
| ± √ 4 · 3 |
| 2 |
x1;2 =
| ± 2√ 3 |
| 2 |
x1;2 = ±√ 3
| x1 = √ 3 | x2 = − √ 3 |
Как найти при каких значениях « x » квадратичная функция принимает заданное числовое значение
Чтобы найти при каких значениях « x » квадратичная функция принимает заданное числовое значение, нужно:
При каких значениях « x » функция принимает значение « −3 ».
Подставим в исходную функцию вместо « y = −3 » и найдем « x ».
−3 = x 2 − x − 3
x 2 − x − 3 = −3
x 2 − x − 3 + 3 = 0
x 2 − x = 0
x1;2 =
| 1 ± √ 1 2 − 4 · 1 · 0 |
| 2 · 1 |
x1;2 =
| 1 ± √ 1 |
| 2 |
x1;2 =
| 1 ± 1 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 1 | x2 = 0 |
Как найти координаты точек пересечения параболы и прямой
Чтобы найти точки пересечения параболы с прямой нужно:
Найти координаты точек пересечения параболы « y = x 2 » и прямой « y = 3 − 2x ».
Приравняем правые части функций и решим полученное уравнение относительно « x ».
x 2 = 3 − 2x
x 2 − 3 + 2x = 0
x 2 + 2x − 3 = 0
x1;2 =
| 2 ± √ 2 2 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
| 2 ± √ 4 + 12 |
| 2 |
x1;2 =
| 2 ± √ 16 |
| 2 |
x1;2 =
| 2 ± 4 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 3 | x2 = −1 |
Теперь подставим в любую из заданных функций (например, в полученные числовые значения « x », чтобы найти координаты « y » точек пересечения.
1) x = 3
y = 3 − 2x
y(3) = 3 − 2 · 3 = 3 − 6 = −3
(·) A (3; −3) — первая точка пересечения.
2) x = −1
y = 3 − 2x
y(−1) = 3 − 2 · (−1) = 3 + 2 = 5
(·) B (−1; 5) — вторая точка пересечения.
Запишем полученные точки пересечения с их координатами в ответ.
Как определить, принадлежит ли точка графику функции параболы
Чтобы проверить принадлежность точки параболе нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси « Ox » вместо « x », а координату по оси « Oy » вместо « y ») и выполнить арифметические расчеты.
Как найти точки пересечения параболы с осями координат
Найти координаты точек пересечения параболы с осями координат.
Сначала определим точки пересечения функции с осью « Ox ». На графике функции эти точки выглядят так:
Как видно на рисунке выше, координата « y » точек пересечения с осью « Ox » равна нулю, поэтому подставим « y = 0 » в исходную функцию « y = x 2 −3x + 2 » и найдем их координаты по оси « Ox ».
0 = x 2 −3x + 2
x 2 −3x + 2 = 0
x1;2 =
| 3 ± √ 3 2 − 4 · 1 · 2 |
| 2 · 1 |
x1;2 =
| 3 ± √ 9 − 8 |
| 2 |
x1;2 =
| 3 ± √ 1 |
| 2 |
x1;2 =
| 3 ± 1 |
| 2 |
x1 =
| x2 =
| ||||
x1 =
| x2 =
| ||||
| x1 = 2 | x2 = 1 |
Теперь найдем координаты точки пересечения с осью « Oy ».
Как видно на рисунке выше, координата « x » точки пересечения с осью « Oy » равна нулю.
Подставим « x = 0 » в исходную функцию « y = x 2 −3x + 2 » и найдем координату точки по оси « Oy ».
y(0) = 0 2 − 3 · 0 + 2 = 2
Выпишем координаты полученной точки: (·) C (0; 2)
Запишем в ответ все координаты точек пересечения параболы с осями.
Как определить при каких значениях x функция принимает положительные или отрицательные значения
Чтобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:
С помощью графика квадратичной функции, изображенного на рисунке, ответить: При каких значениях « x » функция принимает 1) положительные значения; значения.
Проведем через точки, где график функции пересекает ось « Ox » прямые.
Определим области, где функция принимает отрицательные или положительные значения.
Подпишем над каждой полученной областью, какие значения принимает « x » в каждой из выделенных областей.
Ответ: при « x » и « x > 2 » функция принимает отрицательные значения; при функция принимает положительные значения.
Точки пересечения графика функции с осями координат
Точки пересечения графиков функций
В алгебре и начале анализа можно встретить множество задач на поиск точек пересечения графиков функций с помощью их построения или другими методами. Благодаря определенному алгоритму действий, найти ответ достаточно просто. В большинстве случаев решение заключается в определении корней различного вида уравнений.
Равенство \(y = f(x)\) называют уравнением данного графика. Таким образом, график функции представляет собой множество точек (x; y), где x — является аргументом, а y — определяется как значение функции, соответствующее данному аргументу.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В том случае, когда графики пересекаются в какой-то точке, можно сделать вывод о существовании общего решения системы уравнений. Определить координаты точки можно с помощью графического или аналитического метода. В первом случае требуется построить график уравнения с переменной. Аналитический метод поиска координат точек, в которых графики функций пересекаются, подразумевает решение уравнения, а найденные корни и являются искомыми точками.
Как найти координаты, примеры решения
Существует несколько способов решения подобных задач:
В качестве примера можно рассмотреть две линейные функции:
Имеются функции: \(f(x) = 2x-5\)
Требуется определить координаты точки, в которой пересекаются графики рассматриваемых функций.
В первую очередь стоит отметить, что функции являются линейными. Важно обратить внимание на коэффициент угла наклона рассматриваемых функций:
По этой причине имеется лишь одна точка пересечения графиков функций. Определить ее можно путем решения уравнения:
Таким образом, M (8;11) – представляет собой точку, в которой пересекаются графики пары линейных функций.
Записаны две функции: \(f(x)=2x-1\)
Необходимо определить точки, в которых графики рассматриваемых функций пересекаются.
Таким образом, линейные функции параллельны между собой, что объясняет отсутствие точек пересечения их графиков.
Ответ: графики функций параллельны, точки пересечения отсутствуют.
Требуется определить координаты точки, в которой пересекаются графики следующих функций: \(f(x)=x^2-2x+1\)
В данном случае функции являются нелинейными. Поэтому алгоритм решения задачи будет несколько отличаться от предыдущих примеров. В первую очередь следует приравнять уравнения:
Далее необходимо разнести в разные стороны уравнения члены с x и без него:
Таким образом, будет определена абсцисса искомой точки. Затем необходимо найти ординату у. Для этого нужно подставить \(x = 0\) в какое-либо из двух начальных уравнений. К примеру:
M (0;1) является точкой, в которой пересекаются графики функций.
Приравнивание функций друг к другу и нахождение корней
Выяснить, имеют ли точки пересечения графики функций, можно путем сравнения соответствующих тождеств и решения уравнения. Однако при этом допускается получение различных равенств с неизвестными. Тогда целесообразно воспользоваться специальными методиками.
Когда уравнение относится к первой степени или является линейным, решение получить достаточно просто. Метод заключается в переносе переменных величин в одну часть уравнения, а известных – в другую. Алгоритм действий:
Квадратные уравнения решают с помощью одного из способов:
В первом случае представляется возможным понизить степень при неизвестной величине. Второй метод заключается в выделении квадрата по одной из формул сокращенного умножения. Каждая из этих методик реализуема при наличии знаний соответствующих тождеств, в том числе правил разложения на множители.
Третий способ состоит в поиске корней через дискриминант (Д), который является дополнительным параметром, позволяющим сразу решить задачу. Дискриминант определяется с помощью формулы:
В том случае, когда Д>0, переменная может иметь пару значений, которые превращают равенство в справедливое тождество. Если Д=0, то корень является единственным. Когда Д Примечание
Распространенной ошибкой является пренебрежение проверкой результатов решения. Некорректные действия могут привести к образованию ложных корней.
Существует несколько методик решения тождеств кубического и биквадратного типов:
Первый вариант решения подразумевает выполнение преобразований для последующего применения одной из формул сокращенного умножения. Такой способ применяют нечасто. Второй способ состоит в том, что при решении необходимо ввести переменную с более низкой степенью, которая упрощает выражение. Порядок действий при этом следующий:
Путем составления системы уравнений
Данный метод определения точек пересечения графиков функций предполагает запись системы уравнения. К примеру:
Решение системы уравнений представляет собой пару чисел (х, у), являющуюся одновременно решением для первого и второго уравнения системы. Решить систему уравнений – значит, отыскать все ее решения, либо установить их отсутствие.
Порядок действий при решении системы уравнений можно рассмотреть на примере:
Решение будет иметь следующий вид:
Решение системы представляет сбой единственную пару чисел:
Если подставить данные числа в любое из уравнений, то получится справедливое равенство. Таким образом, имеется единственное решение линейной системы. Можно записать отчет: (-1;0).
В процессе решения линейной системы можно столкнуться с разными ситуациями:
При рассмотрении частного случая системы p(x; y) и q(x; y) являются линейными выражениями от x и y.
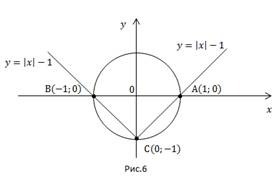
В задачах нередко требуется решить нелинейную систему уравнений. К примеру, необходимо решить следующую систему:
Решение имеет следующий вид:
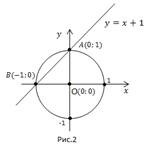
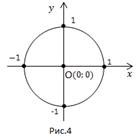
График первого уравнения будет иметь вид прямой, а второго – являться окружностью. Можно построить первый график по точкам:
Центр окружности в точке О(0; 0), радиус равен 1.
Графики пересекаются в точке А(0; 1) и в точке В(-1; 0).
Можно решить систему графическим способом:
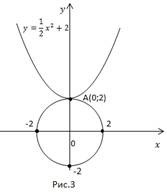
В первую очередь необходимо построить график первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 2. График второго уравнения является параболой, которая смещена относительно начала координат на 2 вверх, то есть ее вершина – точка (0; 2).
Графики обладают одной общей точкой А(0; 2). Данная точка является решением системы. Если подставить два числа в уравнение, можно проверить корректность ответа и записать его. Ответ: (0; 2).
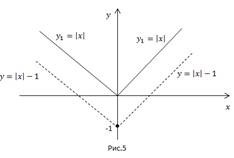
В качестве еще одного примера можно решить следующую систему:
Первым шагом является построение графика первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 1.
Далее необходимо построить график функции:
График будет являться ломанной:
Далее следует сместить ее на 1 вниз по оси oy. В результате получится график функции:
При помещении обоих графиков в одну систему координат получится следующая ситуация:
Нахождение через графическое построений функций
Любой определенный график задают с помощью соответствующей функции. Найти точки, в которых пересекаются графики, можно путем решения уравнения, имеющего вид:
Решение данного уравнения будет являться искомой точкой.
Построить график можно с помощью бумаги и ручки. В процессе необходимо обратить внимание на то, что количество точек пересечения пары графиков определяется видом функции. Линейные функции обладают лишь одной точкой пересечения, линейная и квадратная – двумя, квадратные – двумя, либо четырьмя.
В общем случае двух линейных функций можно предположить, что:
Для поиска точки пересечения графиков необходимо решить уравнение:
\(y1=y2 \ или \ k1x+b1=k2x+b2\)
После преобразований получится, что:
Далее нужно выразить x:
При известной координате точки по оси абсцисс следует определить координату по оси ординат. Таким образом, можно найти координаты точки пересечения графиков:
График функции y = f (х) представляет собой множество точек плоскости, координаты (х, у) которых соответствуют выражению y = f(x). График функции наглядно иллюстрирует поведение и свойства функции. Для построения графика определяют несколько значений довода х и для них рассчитывают соответствующие значения функции y=f(x). Для больше точного и наглядного построения графика следует обнаружить его точки пересечения с осями координат.
С целью определить точку пересечения графика функции с осью y, нужно определить значение функции при х=0, то есть обнаружить f(0). В качестве примера можно рассмотреть график линейной функции, изображенной на рисунке: