Как понять что функция общего вида
Виды функций (четные, нечетные, общего вида, периодические функции)
Глава 1. Развитие понятия функции
Изучение свойств функции и построение ее графика являются одним из самых замечательных приложений производной. Этот способ исследования функции неоднократно подвергался тщательному анализу. Основная причина состоит в том, что в приложениях математики приходилось иметь дело со все более и более сложными функциями, появляющимися при изучении новых явлений. Появились исключения из разработанных математикой правил, появились случаи, когда вообще созданные правила не годились, появились функции, не имеющие ни в одной точке производной.
Развитие функциональных представлений в курсе изучения алгебры и начал анализа на старшей ступени обучения помогает получить наглядные представления о непрерывности и разрывах функций, узнать о непрерывности любой элементарной функции на области ее применения, научиться строить их графики и обобщить сведения об основных элементарных функциях и осознать их роль в изучении явлений реальной действительности, в человеческой практики.
Начиная с XVIII века одним из важнейших понятий является понятие функции. Оно сыграло и поныне играет большую роль в познании реального мира.
Необходимые предпосылки к возникновению понятия функции были созданы, когда возникла аналитическая геометрия, характеризующаяся активным привлечением алгебры к решению геометрических задач.
Идея функциональной зависимости возникла в глубокой древности. Она содержится уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами, в первых формулах для нахождения площади и объема тех или иных фигур и геометрических тел.
Однако явное и вполне сознательное применение понятия функции и систематическое изучение функциональной зависимости берет свое начало в XVII веке в связи с проникновением в математику идеи переменных.
Четкого представления понятия функции в XVII веке еще не было, однако путь к первому такому определению проложил Декарт. Постепенно понятие функции стало отождествляться с понятием аналитического выражения – формулы.
Явное определение функции было впервые дано в 1718 году Иоганном Бернулли: «Функцией переменной величины называют количество, образованное каким угодно способом из этой переменной величины и постоянных».
Во второй половине XIX века понятие функции формулируется следующим образом: если каждому элементу х множества А поставлен в соответствие некоторый определенный элемент у множества В, то говорят, что на множестве А задана функция y = f(x), или что множество А отображено на множество В.
Общее понятие функции применимо, конечно, не только к величинам и числам, но и к другим математическим объектам, например, к геометрическим фигурам.
Краткий обзор развития понятия функции приводит к мысли о том, что эволюция еще далеко не закончена и, вероятно, никогда не закончится, как никогда не закончится и эволюция математики в целом.
Глава 2. Основные свойства функции
Определение функции и графика функции. Область определения и область значений функции. Нули функции
функция график экономический
Умение изображать геометрически функциональные зависимости, заданные формулами, особенно важно для успешного усвоения курса высшей математики.
Как известно, функциональной зависимостью называют закон, по которому каждому значению величины х из некоторого множества чисел, называемого областью определения функции, ставится в соответствие одно вполне определенное значение величины у; совокупность значений, которые принимает зависимая переменная у, называется областью изменения функции.
Независимую переменную х называют также аргументом функции. Число у, соответствующее числу х, называют значением функции f в точке х и обозначают f(x).
Функцию можно задать тремя способами: аналитический, табличный, графический.
Аналитический – с помощью формул.
Табличный – с помощью таблиц, где можно указать значения функции, однако лишь для конечного набора значений аргумента.
Графический способ задания функции очень удобен: он дает возможность наглядно представить свойства функции.
Графиком функции f называют множество всех точек (х;у) координатной плоскости, где y=f(x), а х «пробегает» всю область определения функции f.
Пример 1. Найти область определения функции
y = lg (2x-3) у = lg(2x-3)
Одним из понятий для исследования функции является нули функции.
Нули функции – это точки, в которых функция принимает значение нуля.
Глава 39. Понятие функции. Основные свойства функций
Постоянной величиной называется величина, сохраняющая одно и тоже значение.
Например, отношение длины окружности к ее диаметру есть постоянная величина, равная p.
Если величина сохраняет постоянное значение лишь в условиях данного процесса, то в этом случае она называется Параметром.
Переменной называется величина, которая может принимать различные числовые значения.
Например, при равномерном движении S = vt, где путь S и время t – переменные величины, а v – параметр.
Если каждому элементу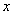 
множества 
( 
) ставится в соответствие вполне определенный элемент 
множества 
( 
), то говорят, что на множестве задана Функция 
.
При этом 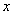называется Независимой переменной (или аргументом), –зависимой переменной, А буква 
обозначает закон соответствия.
Множество Называется Областью определения (или Существования) функции, а множество – Областью значений функции. Если множество специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной , т. е. множество таких значений , при которых функция вообще имеет смысл.
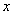
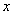
Например, область определения функции 
есть полуинтервал 
, так как 
; если же переменная обозначает, предположим, время, то при естественном дополнительном условии 
областью определения функции будет отрезок 
.
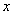
Способы задания функций
Задать функцию – значит Указать закон, по которому, согласно определению, каждому значению аргумента из области определения ставится в соответствие значение функции из области значений функций. Существует три основных способа задания функций: Табличный, аналитический и графический.
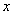
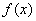
Табличный способ Состоит в том, что функция задается таблицей, содержащей значения аргумента И соответствующие значения функции 
, например таблица логарифмов. Табличный способ имеет широкое применение в различных отраслях знаний и приложениях: ряды экспериментальных измерений, социологические опросы, таблицы бухгалтерской отчетности и банковской деятельности и т. п.
Аналитический способ состоит в задании связи между аргументом и функцией в виде формул. Этот способ наиболее часто встречается на практике. Так, функция , рассматриваемая выше, задана аналитически. Не следует смешивать функцию с ее аналитическим выражением. Так, например, одна функция
Имеет два аналитических выражения, используемых при различных значениях аргумента.
Графический способ Состоит в том, что соответствие между аргументом и функцией задается посредством графика. Этот способ обычно используется в экспериментальных измерениях и употреблением самопишущих приборов (осциллографы, сейсмографы и т. д.).
Основные свойства функции
1. Четность и нечетность.
Функция называется Четной, если для любых значений из области определения 
И Нечетной, Если 
. В противном случае функция называется функцией Общего вида.
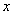
Например, функция 
является четной, а функция 
– нечетной. Функция 
является функцией общего вида, так как 
и 
И 
.
График четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.
Функция называется Возрастающей (Убывающей) на промежутке , если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Пусть 
и 
. Тогда функция возрастает на промежутке X, если 
и убывает, если 
.
Функции возрастающие и убывающие называются Монотонными функциями.
Так, например, функция при 
убывает и при 
– возрастает.
Функция называется Ограниченной на промежутке X, если существует такое положительное число M>0, что 
Для любого .
Например, функция 
ограничена на всей числовой оси, так как 
для любого 
.
Функция Называется Периодической с периодом 
, если для любых X из области определения функции 
.
Например, функция имеет период 
, так как для любых 
.
Четные и нечетные функции
Вы будете перенаправлены на Автор24
Четные функции
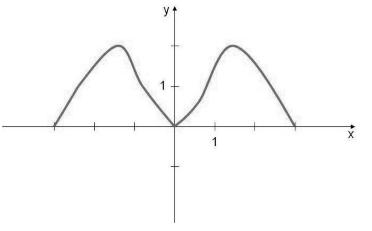
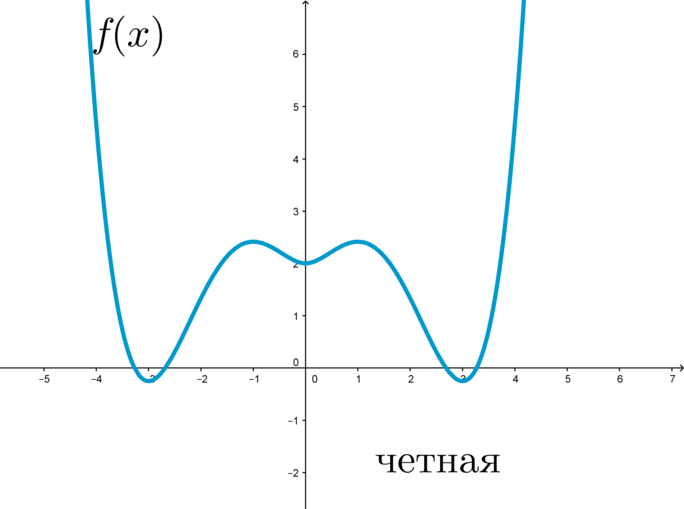
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будет совпадать, то график этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).
Нечетные функции
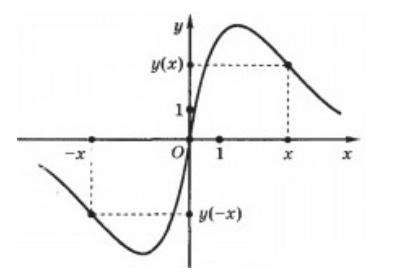
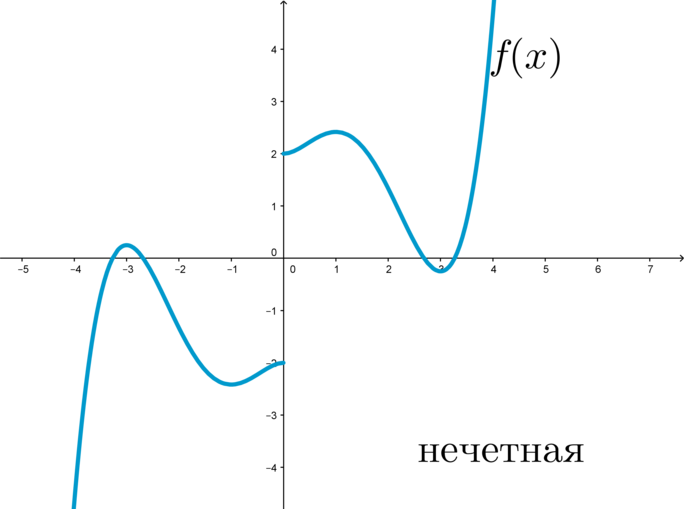
Так как при выборе равных по модулю с обоими знаками значений независимых переменных для любой четной функции значения самой функции будут также совпадать по модулю и отрицательны по знакам, то график этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).
Готовые работы на аналогичную тему
Функция общего вида
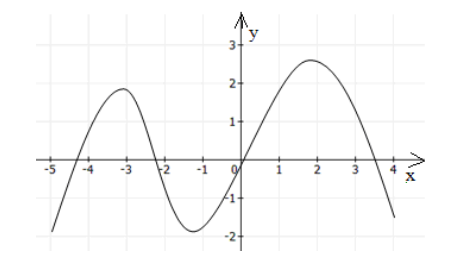
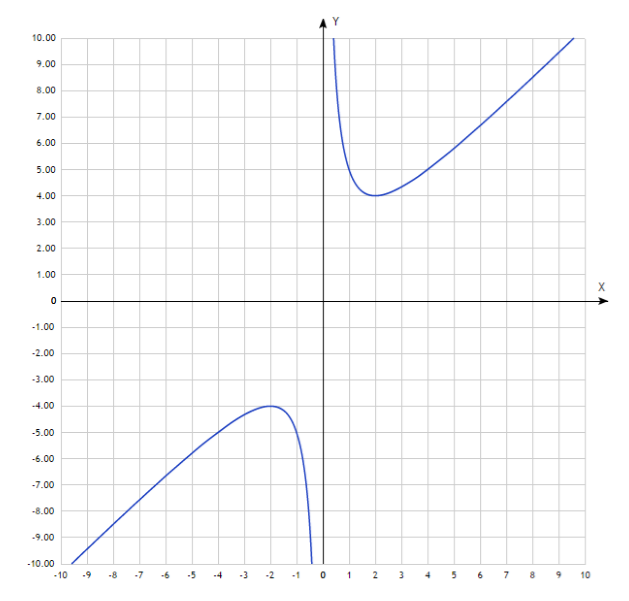
Функция общего вида никогда не будет симметрична оси ординат и началу координат. Пример функции общего вида изображен на рисунке 3.
Пример задачи
Исследовать функцию на четность и нечетность и построить их графики.
Изобразим её на графике:
Изобразим её на графике:
Изобразим её на графике:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 04 07 2021
Четные и нечетные функции
График четной функции симметричен относительно оси \(y\) :
График нечетной функции симметричен относительно начала координат:
\(\blacktriangleright\) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
\(\blacktriangleright\) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
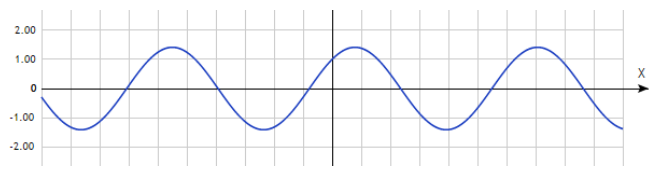
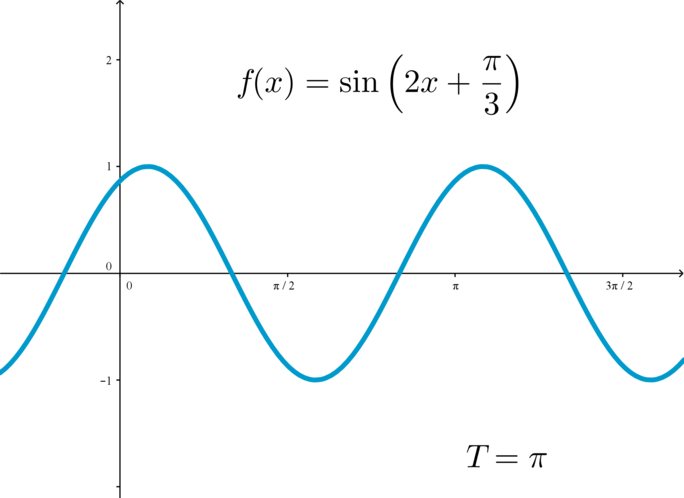
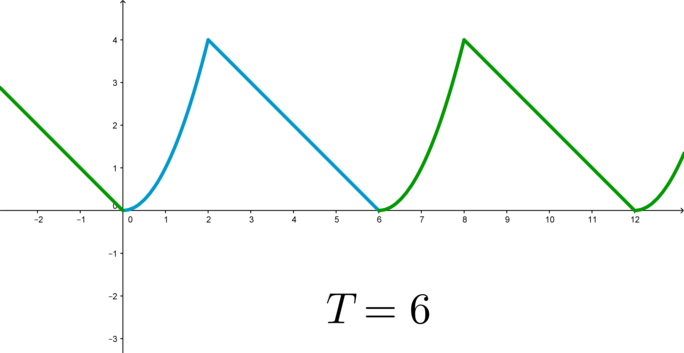
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной \(T\) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:
При каких значениях параметра \(a\) уравнение
имеет единственное решение?
\[2\cdot 0+a\mathrm
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)
\(\dfrac n2, n\in\mathbb
(Задача от подписчиков)
имеет хотя бы один корень.
(Задача от подписчиков)
имеет шесть различных решений.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \[D=a^2-16a+52>0\quad\Leftrightarrow\quad a\in (-\infty;8-2\sqrt3)\cup(8+2\sqrt3;+\infty)\]
2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: \[\begin
Функция
1. Понятие функции
2. Cвойства функций
2.Монотонность. Функция называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции, т.е. при x1 ) x2, f(x1) ) f(x2).
область определения (-∞,∞)
область значений (0; ∞)
общего вида
возрастает на (-∞,∞), если a>1;
убывает на (-∞,∞), если 0 непериодическая
Логарифмическая функция
у = log ₐ x (a>0 a≠1)
область определения (0,∞)
область значений (-∞; ∞)
общего вида
возрастает на (0,∞), если a>1;
убывает на (0,∞), 0 непериодическая
Тригонометрические функции
y = sin x
область определения (-∞; ∞)
область значений [-1; 1]
нечетная
возрастает на [-π/2 + 2πn, π/2 + 2πn];
убывает на [π/2 + 2πn, 3π/2 + 2πn], nϵZ;
период Т=2π
y = cos x
область определения (-∞; ∞)
область значений [-1; 1]
четная
возрастает на [-π + 2πn, 2πn];
убывает на [2πn, π + 2πn], nϵZ;
период Т=2π
y = tg x
область определения
(-π/2 + πn, π/2 + πn) nϵZ;
область значений (-∞; ∞)
нечетная
возрастает на (-π/2 + πn, π/2 + πn) nϵZ;
период Т=π
y = ctg x
область определения
(πn, π + πn) nϵZ;
область значений (-∞; ∞)
нечетная
убывает на (πn, π + πn) nϵZ;
период Т=π
y = arcsin x
область определения [-1; 1]
область значений [-π/2; π/2]
нечетная
возрастает на [-1; 1]
y = arccos x
область определения [-1; 1]
область значений [0; π]
функция центрально-симметрична относительно точки (0; π/2)
убывает на [-1; 1]
y = arctg x
область определения (-∞; ∞)
область значений [-π/2; π/2]
нечетная
возрастает на (-∞; ∞)
y = arcctg x
область определения (-∞; ∞)
область значений [0; π]
ни четная, ни нечетная
убывает на (-∞; ∞)