Как понять что такое матрица

Что такое матрицы, откуда они взялись, и чем они полезны?

Первые упоминания о матрицах или «волшебных квадратах», как их тогда называли, были найдены на территории еще Древнего Китая, однако бум случился намного позже, в середине XVIII века, когда знаменитый математик Габриэль Крамер опубликовал свой труд под названием «Введение в анализ алгебраических кривых», в котором описывался алгоритм решения систем линейных уравнений совершенно новым методом.

Как следствие, в дальнейшем появляются «классический» метод решения Карла Фридриха Гаусса, теорема Гамильтона-Кели, работы Карла Вейерштрасса, Георга Фробениуса и других выдающихся ученых.

Занимательно, что только после всех этих открытий, а именно в 1850 году был непосредственно введен термин матрица, автором которого стал Джеймс Джозеф Сильвестр.

Сегодня термин «матрица» применяется во множестве разных областей: от программирования до кинематографии (здесь должно быть название фильма, о котором вы все подумали).

Матрица в математике – это таблица чисел, состоящая из определенного количества строк (m) и столбцов (n).

Вы встречаетесь с ними каждый день, так как любая числовая информация, занесенная в таблицу, уже в какой-то степени считается матрицей.

Примером могут служить:
● список телефонных номеров;
● различные статистические данные;
● табель успеваемости ученика и многое другое.

Сами матрицы всегда обозначаются прописными латинскими буквами (A, B, C…), а элементы матрицы – строчными (a, b, c…). Индексы обозначают местоположение элемента матрицы в системе, причем первое число – это всегда номер строки, а второе – это всегда номер столбца. Например, а₂₃ находится во второй строке и в третьем столбце, а₃₁ в третьей строке и первом столбце и т.д.

Важно произносить элементы матриц правильно, так а₂₃ будет звучать как «а два три», а не «а двадцать три».

Примеры записи матриц

Для чего нужны матрицы

Теперь выясним, для чего нам так нужны матрицы конкретно в математике?

В качестве примера рассмотрим простейшую систему двух линейных уравнений и решим ее методом сложения, который изучают в школьном курсе.

Оказывается, можно решить эту систему уравнений альтернативным способом, используя матрицы, и называется он метод Крамера.

Вы можете подумать, зачем усложнять решение какими-то матрицами?

В данном случае да, при желании можно эту систему и в уме решить. Но представьте себе систему, состоящую хотя бы из 5 линейных уравнений с пятью неизвестными. А если система состоит из 6, 7 или ещё больше уравнений? Решать её школьным методом, мягко говоря, трудоёмко. Зато применяя тот же метод Крамера, решение будет выглядеть достаточно компактно.

Система с тремя уравнениями

В подтверждение вышесказанного рассмотрим систему уравнений с тремя неизвестными и решим её метод Крамера.

Из этого следует, что матрицы – еще один способ решения систем линейных алгебраических уравнений (СЛАУ).

На основе второго примера убеждаемся в том, что матрицы могут применяться в тех случаях, когда применение школьных методов решения СЛАУ не является рациональным.

На самом деле за прошедшие столетия алгебра матриц изучена более, чем достаточно, и тот факт, что матрицы используются повсеместно однозначно подтверждает необходимость их изучения.

Источник

Значение слова «матрица»

1. Тех. Углубленная металлическая форма, применяемая при обработке металла давлением, при отливке типографских литер и пр. Линотипная матрица.

2. Типогр. Обратная (углубленная) копия, снимаемая с набора на картоне, свинце, пластмассе и т. п. для отливки стереотипов, с которых производится печатание.

3. Мат. Система каких-л. математических величин, расположенных в виде прямоугольной схемы.

[От лат. matrix, matricis — матка]

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Матрица (искусство и техника) — образец, модель, штамп, шаблон, инструмент в серийном производстве объектов искусства и техники.

Матрица (диск) — название специального диска, служащий образцом для создания дисков (компакт-диск, DVD и др.) с записью (музыки, фильмов и т. д.) при их серийном или массовом производстве.

Матрица (издательское дело) — вогнутая часть формы, в которой пластическое тело формуется давлением, служащее типографским шрифтом.

Матрица в красильном деле — деревянная пластинка с вырезанным на ней рельефом какого-нибудь узора, служащая для отливки металлических набивных форм.

Матрица композита — связующее композиционного материала: распределяет нагрузку по армирующим элементам и защищает их.

Матрица как прямоугольная таблица:

Матрица (математика) — прямоугольная таблица элементов некоторого кольца или поля.

Матрица (программирование) — двумерный массив.

Матрица (электроника) — обобщенный термин для различных объектов в электронике, в которых элементы объекта упорядочены в виде двумерного массива, аналогично математической матрице.

Мáтричный индикáтор — разновидность знакосинтезирующего индикатора, в котором элементы индикации сгруппированы по строкам и столбцам.

Матрица (фото) — полупроводниковая СБИС с прямоугольной матрицей светочувствительных элементов (фотодиодов) для преобразования поступающего на неё света (отраженного от объекта) в электронный сигнал (изображение) или массив цифровых данных.

Матрица (экономика) — таблицы, предназначенные для диагностики состояния.

МА’ТРИЦА, ы, ж. [нем. Matrize] (тех.). 1. Пластинка с выдавленными, вырезанными обратными знаками или изображениями чего-н., служащая формой для отливки или штамповки. С матриц отливают типографские литеры. Матрицы употребляются при чеканке монеты. 2. Бумажная форма, являющаяся обратной копией набора и служащая для отливки стереотипа (тип.). Печатать что-н. с матриц.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

ма́трица

1. техн. форма с углубленным изображением рисунка, используемое во многих технологических процессах

2. техн. система каких-либо элементов, расположенных прямоугольником ◆ Матрица светочувствительных элементов.

3. матем. математический объект в виде таблицы чисел (или других сходных математических объектов) ◆ Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной.

Фразеологизмы и устойчивые сочетания

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: вить — это что-то нейтральное, положительное или отрицательное?

Источник

lsvsx

Всё совершенно иначе!

Истина где-то посередине. Так давайте подгребать к ней не теряя достоинства.

Фильм «Матрица» вышел не так давно и уже снискал себе огромную славу. Он даже успел стать культовым фильмом нашего времени. Удивительно, но как точно авторы фильма увидели многие тонкие философские моменты, которые пытались передать людям и «просветленные” мира сего и многие великие философы.

Мы в ловушке. Этим миром правят жестокие и бездушные машины, а нас они используют просто в качестве «батареек».

Большинство зрителей, конечно, скоро оправятся от этого шока и снова «поверят” в реальность происходящего.

Они будут есть, пить, веселиться, уверенные в том, что это и есть настоящая жизнь.

В чем философия Вед и Матрицы?

Синяя таблетка Матрицы

Красная таблетка реальности

Может быть, этот путь также займет не одну жизнь… Но что с того? Никакая цена не будет слишком высокой, ибо ты возвращаешься в реальность, навсегда оставляя путы иллюзии.

Но те, кто выдержит, тем откроется Путь Домой, в намного более прекрасный мир, чем в фильме.

А пока мы еще здесь и витаем над этим миром Матрицы, не будучи уже его частью, нам остается только пытаться раскрыть глаза другим, таким же ищущим истину душам, которые тоже начали догадываться, что «в этом мире что-то не так».

И тогда мы сможем взять эту душу с собою и сказать ей те же слова, которые когда-то сказали нам:

Это верно: только совместные усилия учителя и ученика приводят к успеху.

Вот такой удивительный фильм гуляет сейчас по экранам. Только кто из зрителей действительно поймет глубинный смысл этого фильма? Может быть, ты?

Почему мы попали в Матрицу?

Почему мы находимся в Матрице? А если мы в неё попали, то откуда?

А если можно из неё освободится, то куда направиться? Что для этого нужно?

Мудрецы, духовные учителя прошлого, раскрывали и раскрывают знание, как преодолеть Матрицу. И авторитетом может быть только тот учитель, который получил это знание от своего учителя, полученной по цепи преемственности, начиная от источника всего мироздания – Господа.

Карма как космический закон

В послании Павла говорится: «Что человек посеет, то и пожнёт”.

Поэтому бесполезно и глупо искать ответственных за наше счастье или страдания. Индийская пословица гласит: «Когда я одним пальцем указываю на другого, то три указывают на меня”.

Но, если речь идёт обо всём мире, то необходимо принять существование космических норм добра и зла.

Эти нормы описаны в ведических произведениях и других явленных писаниях. Например, хорошими принимаются такие действия, как возлюбить ближнего своего, помогать тем, кто в беде, не прелюбодействовать и т.д.

Поняв космические нормы морали, человек способен в любой ситуации поступать правильно не на основе относительных правил, а на основе глобальной истины.

В своей жизни мы можем учиться на собственных примерах и ошибках и делать соответствующие выводы.

Каждое событие в нашей жизни должно стать для нас уроком космической морали. Тогда вся жизнь превратится в школу святости и восхождения к Свету, что приведёт нас к самосовершенствованию в течении одной жизни.

Как Матрица удерживает нас

С помощью чего Матрица удерживает нас здесь, в этом мире, который на самом деле является местом страданий?

Почему мы не видим этого? Как и с помощью чего она покрывает наше сознание так, что мы не видим этого? Почему, когда нам говорят об этом, мы не верим этому?

Матрица имеет всего несколько простых инструментов, с помощью которых она крепко удерживает нас в иллюзии.

Это наше желание быть независимым от изначального источника нашего появления – от Бога, и наше желание наслаждаться материальной природой – Матрицей. В конечном итоге эти желания означают только одно – желание самому стать таким своего рода богом, со своими владениями (домом, машиной, и др.), подданными (детьми, женой, подчиненными и т.д), богатствами (счетом в банке, золотом).

Но, ничего не подозревая, мы сами создаем себе прочнейшие цепи и кандалы, с помощью которых Матрица крепко удерживает нас в себе.

Это наши желания сексуальных наслаждений, все большего и большего количества денег и необходимой власти (даже над своей семьей), чтобы все это поддерживать. Как паук плетет себе паутину, так и мы создаем себе сети Матрицы, из которых потом не так-то просто выпутаться.

Эта низшая энергия майа со времен сотворения мира изумляет и завораживает души, равнодушные к Богу, и вводит их в заблуждение.

Ответ – да. Мы сами выбираем ту или иную ситуацию, тот или иной жизненный путь, и в дальнейшем соответственно получаем результаты того, что выбрали раньше. Никто, кроме нас самих, не создает страдания или счастье в нашей жизни. Мы ответственны за все, что происходит с нами, и когда мы начинаем понимать это, то мы становимся способны изменить свою жизнь к лучшему.

Тогда мы начинаем воспринимать все беды и препятствия в нашей жизни как своего рода испытание и жизненные уроки. А Матрица или майа – это энергия Господа, которая помогает нам проходить эти уроки, создавая для нас те или иные ситуации.

Это и есть так называемая школа жизни, через которую мы должны пройти с честью и достоинством и успешно сдать экзамены по ее окончанию.

Тогда мы сможем перейти на следующий уровень своего развития.

В ходе нашего обучения мы начинаем понимать, что все препятствия и помехи нужны для того, чтобы обучить нас и испытать наше усердие и постоянство.

А Матрица, или майа, как энергия Господа, может как стать нашим учителем, помогая нам, так и окончательно запутать нас в сетях наших же бесконечных желаний и их обескураживающих последствий.

В зависимости от нашего выбора мы воспринимаем реальность существования Матрицы, майи или даже Самого Господа. И соответственно формируется наше принятие или непринятие их как существующей реальности, и наше отношение к ним.

Так, например, когда врачи назначают горькие лекарства, диету или вскрывают скальпелем нарыв, то пациент может быть недоволен, полагая, что врач жесток, злонамерен и является его врагом. Но разумный человек понимает, что врач является его истинным благожелателем и только хочет помочь ему выздороветь.

Так и Божественная энергия, майа, погружая нас в различные ситуации и искушая, заставляет нас делать ежесекундный выбор между Добром и злом. Так, проходя эти жизненные уроки, ошибаясь и падая, перерождаясь жизнь за жизнью в различных телах, но, все же, опять поднимаясь и выбирая добро и свет, мы можем окончательно утвердиться в своем выбранном пути вперед, к Божественной Любви.

Матрица в древних источниках

Эта книга была открытием для нас. Мы были поражены, что тысячи лет назад информация о Матрице была известна. Более того, в ней сообщается, что Веды являются инструкцией к Матрице, материальной энергии. В Ведах содержится знание о том, как жить в Матрице так, чтобы жизнь стала освобождением из круговорота рождений и смертей.

Освобождение из Матрицы

Родившись в этом теле, я настолько себя с ним отождествил, что даже когда я говорю про себя, то думаю про это тело.

Что вкладывают Веды в понятие духа и материи?

Как научиться различать эти две энергии? Ответы на эти вопросы мы находим в «Бхагавад-гите»:

Иначе говоря, чтобы постичь разницу между материей и духом и научиться отличать их проявления, следует сначала постичь душу, т.е. себя самого.

Вот что говорит «Бхагавад-гита» по этому поводу: «Мудрецы, узревшие истину, пришли к заключению о бренности несуществующего (материального тела) и о неизменности вечного (души).

Они сделали этот вывод, тщательно изучив природу того и другого».

В своих комментариях на этот стих всемирно известный Духовный Учитель Шрила Прабхупада, пишет:

«Наше постоянно меняющееся тело не может существовать вечно. Современная медицина признает тот факт, что на клеточном уровне тело меняется каждое мгновение; это обусловливает процессы роста и старения. Но вечная душа, несмотря на все изменения, которые происходят с телом и умом, всегда остается неизменной. В этом разница между материей и духом. Понятие «существующий» относится исключительно к духу, а понятие «несуществующий» – к материи. Это утверждают все, кто видит истину».

Веды, как и другие священные писания мира, признают, что этот мир был сотворен в определенный момент времени. Подробности этого процесса, которыми пестрят целые тома ведической литературы, заставят призадуматься даже скептиков.

Действенной причиной творения является материальная природа, создающая все виды жизни и различные условия существования.

Также у сотворенного мира есть и смысловая причина.

Цель, или смысл мироздания состоит в том, чтобы дать живому существу (душе) возможность исполнить свои желания и, пресытившись материальными удовольствиями, постичь свое изначальное положение и вырваться из тьмы этого мира.

Иначе говоря, мы все также являемся причиной создания этого мира.

Изначальной и конструктивной причиной этого мира Веды провозглашают Кришну (по древнеславянски – Крышень), Верховную Личность Бога, Верховного повелителя и Творца всего сущего.

В древнейшей «Брахма-самхите» Кришну-Крышеня называют «причиной всех причин» и главной причиной творения. Это Тот, без кого творение невозможно. Однако способ, которым Он творит, в корне отличается от способов, известных нам.

Дело в том, что Бог не должен делать ничего Сам; для этого у Него существует масса слуг и помощников.

Иначе говоря, Бог действует посредством Своих энергий.

В разных частях ведических писаний мы находим подробные описание процесса творения.

Некоторые из них разнятся между собой, что говорит о том, что творение не происходит один раз в истории, но повторяется снова и снова, каждый раз с некоторыми вариациями.

Условия жизни на этих планетах также разнятся: шесть земных месяцев составляют день на высших планетах, а миллионы лет в аду равняются одной земной секунде.

На высших планетах живут полубоги, предки (человечества) и великие мудрецы, хранители вселенной.

На планетах земного типа живут существа, имеющие человеческий тип тела, а на адских планетах живут свирепые существа, которые пытают грешников.

Таково величие творения Бога, прославляемого в Ведах.

Источник

Знакомство с матрицами

Понятие и базовые операции.

Разработчики нейросетей говорят, что все нейросети — это просто бесконечное перемножение матриц. Мы решили разобраться, что это за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так сложно, как мы думали:

Вектор — это «кирпичик» линейной алгебры. На его основе мы переходим к понятию матрицы.

Что такое матрица

Если вектор — это строка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у любой таблицы, у матрицы есть столбцы и строки. В них сидят какие-то числа. Всё вместе — это математический объект, то есть в каких-то случаях всю эту таблицу можно рассматривать как единое целое и совершать с ним операции.

Матрицы принято обозначать большими буквами латинского алфавита вроде А, В, С, D и так далее.

Числа внутри матрицы называют элементами. Каждый элемент обозначается двумя цифрами: первая цифра указывает на строку, а вторая — на столбец. Это адрес числа внутри матрицы. Например, элемент А₂₃ означает, что нужное число находится во второй строке и третьем столбце. Нумерация элементов нужна для записи формул и устного объяснения того, где находится нужное число в матрице.

В матрице может находиться неограниченное количество строк, столбцов и элементов. Из-за этого матрицы бывают разных видов и могут обладать разными особенностями. Например, если в матрице совпадает число строк и столбцов, то такая матрица называется квадратной.

В этой статье и в следующих материалах мы будем рассматривать разные виды матрицы и постепенно изучим их особенности.

Общая схема матрицы Пример квадратной матрицы с пятью строками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по умолчанию. Например, элементу А₂₃ соответствует число три

Простые операции с матрицами

Вынесение минуса за пределы матрицы. Если внутри матрицы у большинства элементов знак минус, то часто это мешает расчётам или приводит к ошибкам. Чтобы этого избежать, от минуса избавляются. Для этого нужно вынести минус за пределы матрицы и изменить знак всех элементов внутри самой матрицы.

И наоборот: если внутри матрицы у большинства элементов знак минус и перед матрицей стоит минус, то минус можно внести в матрицу.

Выносим минус за пределы матрицы и получаем вместо двадцати одного отрицательного элемента — четыре Перед матрицей минус, и внутри у большинства элементов минус. Вносим минус в матрицу и делаем её удобной для дальнейших вычислений

Умножение матрицы на число. Для умножения матрицы на число достаточно каждый элемент матрицы умножить на это число.

Пример умножения матрицы на число

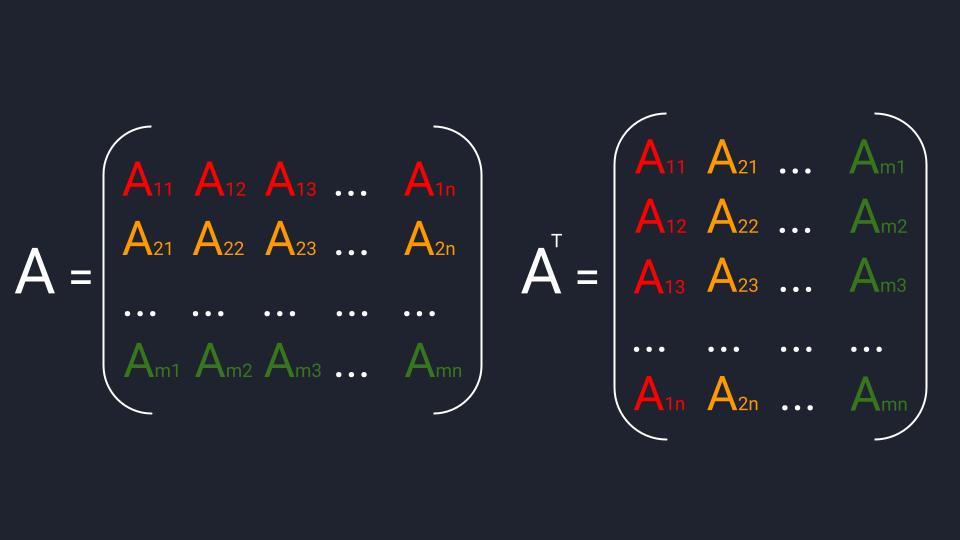
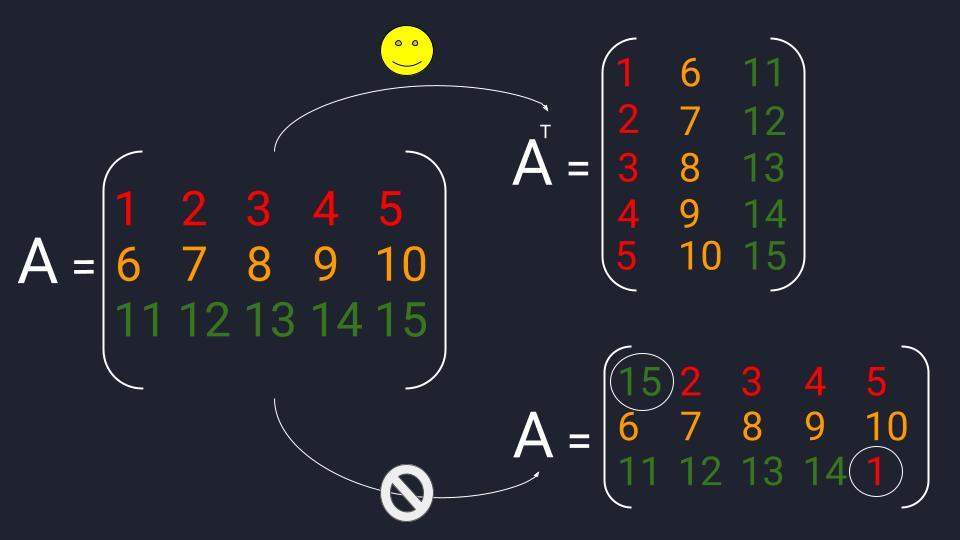
Транспонирование матрицы. Это операция, которая позже нам понадобится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строки со столбцами и получаем новую матрицу. Как бы поставили матрицу набок.

⚠️ При этом в матрице запрещено в произвольном порядке менять элементы. Зато можно полностью менять местами строки или столбцы. Если мы поменяем местами первую и вторую строку, то это останется прежняя матрица.

Схема транспонирования матриц: первая строка переходит в первый столбец, вторая строка — во второй столбец и так далее в зависимости от количества элементов матрицы Пример транспонирования. Транспонированная матрица обозначается буквой той же матрицы, из которой она получилась + надстрочечный индекс в виде печатной буквы «Т» Матрицу можно перетасовывать, но это нужно делать по правилам. Транспонирование — одно из таких правил

Сложение и вычитание матриц

Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их складывать и вычитать. Для вычислений нам нужно поэлементно сложить или вычесть каждый элемент матриц: первый элемент первой матрицы складываем с первым элементом второй матрицы или вычитаем из него и так далее. В результате получаем новую матрицу.

Пример сложения двух прямоугольных матриц с тремя строками и двумя столбцами Пример вычитания двух матриц

Умножение матриц

Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам:

Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.

Формула умножения матриц Пример умножения квадратных матриц размерностью 2×2

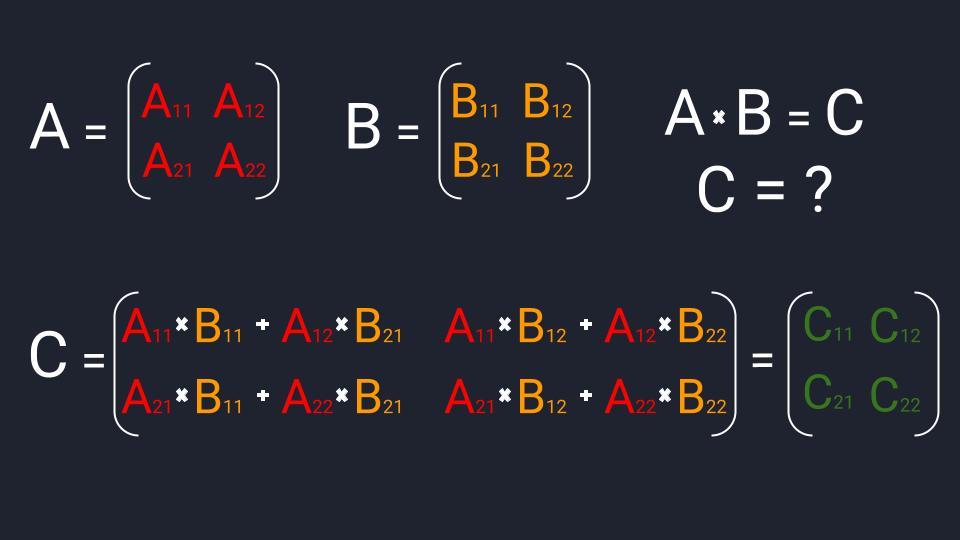
Что дальше

В следующий раз продолжим знакомиться с базовыми понятиями, которые нам понадобятся для решения матричных уравнений. А на сегодня Нео свободен 👽

Источник