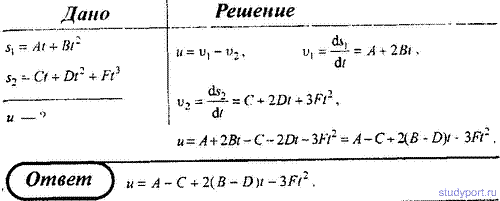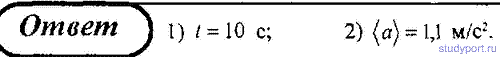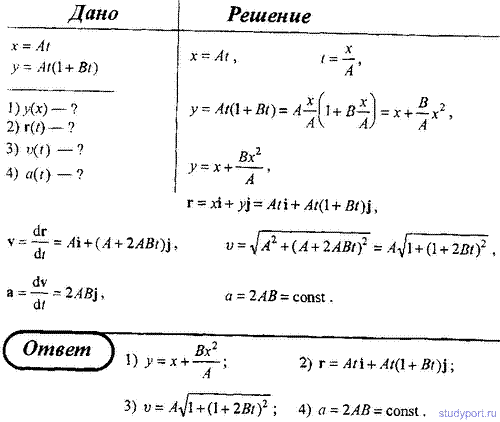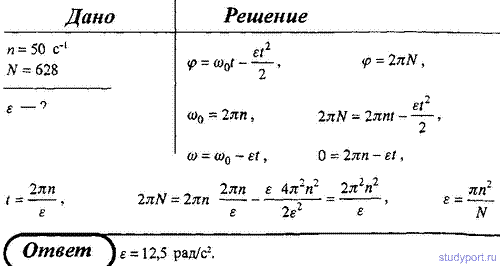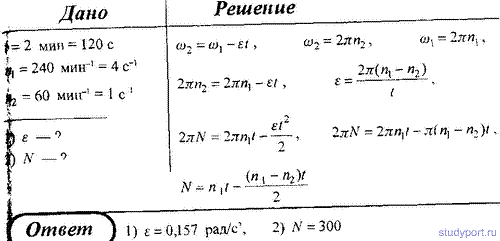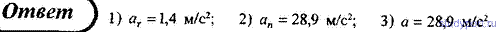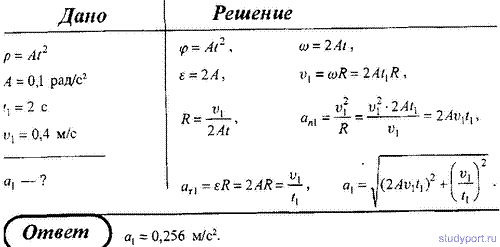Материальная точка движется вдоль прямой так что ее ускорение линейно
1.1 Элементы кинематики
UptoLike
Материальная точка движется вдоль прямой так, что её ускорение линейно растёт и за первые 10 секунд достигает значения 5 м/с2. Определить в конце десятой секунды: 1) скорость точки; 2) пройденный точкой путь.
Тело движется равноускоренно с начальной скоростью v0. Определить ускорение тела, если за время t = 2 с оно прошло путь S = 16 м и его скорость v = 3v0.
Объясните, может ли изменяться направление вектора скорости. в то время как его ускорение по модулю остается постоянным.
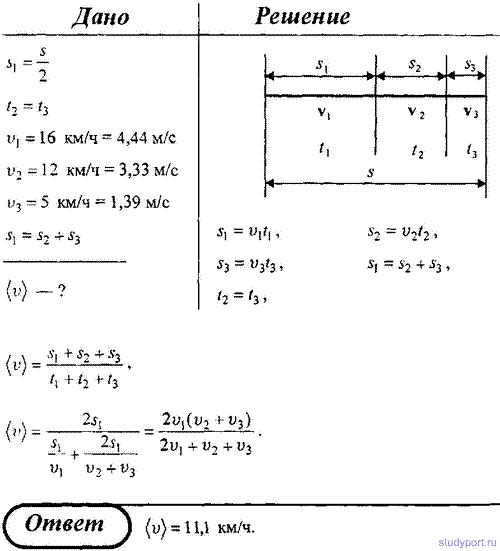
Зависимость пройденного телом пути от времени задается уравнением s(t) = A + Bt + Ct2 + Dt3 (C = 0,1 м/с2, D = 0,03 м/с3) Определите: 1) через сколько времени после начала движения ускорение тела будет равно 2 м/с2; 2) среднее ускорение тела за этот промежуток времени.
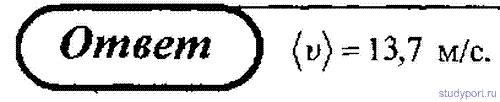
Зависимость пройденного телом пути от времени задается уравнением s(t) = A – Bt + Ct2 + Dt3 (A = 6 м, B = 3 м/с, C = 2 м/с2, D = 1 м/с3) Определить для тела в интервале от t1 = 1 до t2 = 4 с: 1) среднюю скорость; 2) среднее ускорение.
С башни высотой h = 30 м в горизонтальном направлении брошено тело с начальной скоростью v0 = 10 м/с. Определить: 1) уравнение траектории тела y(x); 2) скорость v тела в момент падения на землю; 3) угол φ, который образует эта скорость v с горизонтом в точке его падения.
Тело брошено горизонтально со скоростью v0 = 15 м/с. Пренебрегая сопротивлением воздуха, определить радиус кривизны траектории тела через t = 2 с после начала движения.
С башни высотой H = 40 м в горизонтальном направлении брошено тело с начальной скоростью v0 = 20 м/с под углом α = 45° к горизонту.
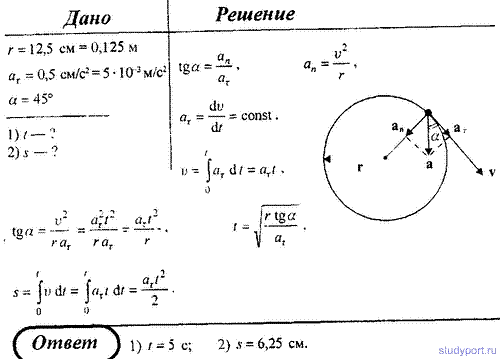
Тело брошено со скоростью v0 = 20 м/с под углом α = 30° к горизонту. Пренебрегая сопротивлением воздуха, определить для момента времени t = 1,5 с после начала движения: 1) нормальное ускорение; 2) тангенсальное ускорение.
Материальная точка движется вдоль прямой так что ее ускорение линейно


Помогите с физикой (до среды) пожалуйста.
| Homka | Дата: Понедельник, 2009-11-09, 9:44 PM | Сообщение # 1 |
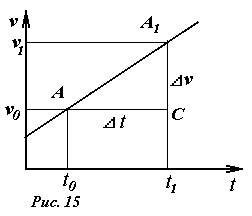
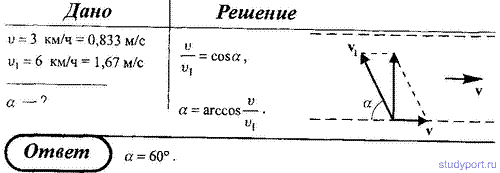
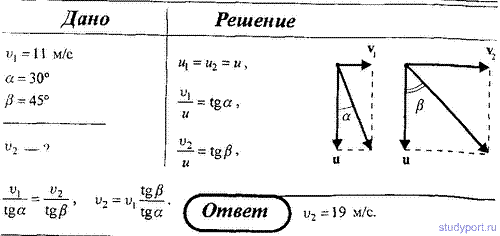
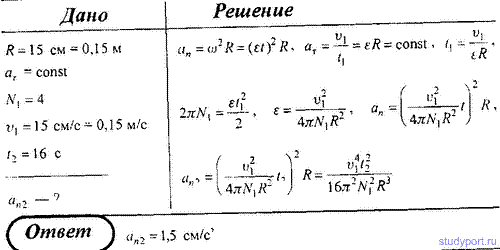
| 1.19 Материальная точка движется вдоль прямой так, что ее ускорение линейно растет, и за первые 10 c достигает значения 5 м/с3. Определить в конце десятой секунды: 1) скорость точки; 2) пройденный точкой путь. Ответ: 1) 25 м/с; 2) 83,3 м. 2.19Стальной шарик массой m = 20 г, падая с высоты h1 = 1 м на стальную плиту, отскакивает от нее на высоту h2 = 81 см. Найти импульс силы F Δt, полученный плитой за время удара, и количество теплоты Q, выделившейся при ударе. Ответ: 0,17 нс; 37,2•10-3 Дж. 2.28Поезд массой m = 600 т движется под гору с уклоном α = 0,3° и за время t = 1 мин развивает скорость υ = 18 км/ч. Коэффициент трения f = 0,01. Определить среднюю мощность локомотива. Ответ: 195 кВт. 5.12Определить отношение кинетической энергии Т точки, совершающей гармонические колебания, к ее потенциальной энергии П, если известна фаза колебания. Ответ: tg2(ω0t + φ). УчебникиЖурнал «Квант»Общие§2. Кинематическое описание механического движения материальной точки2.7 Равноускоренное движение точки по прямойПусть материальная точка движется вдоль заданной прямой линии так, что ее ускорение остается постоянным. Такое движение точки называется равноускоренным [1] или равнопеременным движением. По-прежнему, направим ось X вдоль прямой, по которой движется точка, и введем обычным образом координаты на этой прямой. Используя определение ускорения и учитывая, что при постоянном ускорении это отношение не зависит от значения интервала времени, мы можем выразить значение скорости в произвольный момент времени t Графиком зависимости скорости от времени при равноускоренном движении (то есть графиком функции (2)) является прямая линия, проходящая через точку A с координатами (t0,υ0), коэффициент наклона которой равен ускорению точки (рис.15). При выводе этого соотношения мы учли, что \( Вернемся к цепочке преобразований (3). Из уравнения (2) следует \( Рассмотрим подробнее характер движения при различных значениях параметров равноускоренного движения. Выбор начала отсчета времени, как и выбор начала отсчета координаты произволен, поэтому при изучении движения одного тела, мы можем положить [2] t0 = 0 и x0 = 0. Таким образом рассмотрим закон движения в форме При этом скорость тела изменяется по закону Рассмотрим несколько частных случаев. Тем не менее, модель равноускоренного движения также является приближенной. Если в названных примерах сопротивление воздуха играет существенную роль, то ускорение тел будет заметно изменяться, поэтому модель равноускоренного движения окажется неприменимой. Материальная точка движется вдоль прямой так что ее ускорение линейноНа рисунке приведён график зависимости модуля средней скорости Vр материальной точки от времени t при прямолинейном движении. Из приведённого ниже списка выберите все правильные утверждения и укажите их номера. 3) За первые 3 с движения материальная точка проходит путь 8 м. 4) За первые 2 с движения материальная точка проходит путь 12 м. 5) Модуль начальной скорости материальной точки равен 2 м/с. При равноускоренном движении средняя скорость равна полусумме начальной и конечной скорости. Найдем, чему равна скорость тела в момент времени t = 1 c: Таким образом, ускорение тела равно Путь — это произведение средней скорости на затраченное время Обратите внимание, что на графике приведена зависимость средней скорости от времени, а не просто скорости. Наклон этого графика не равен ускорению. Грузик массой m = 100 г неподвижно висит на лёгкой абсолютно упругой гибкой резинке с коэффициентом упругости k = 100 Н/м в поле силы тяжести с ускорением свободного падения g. Грузик поднимают из этого положения вертикально вверх на высоту h = 80 см, меньшую длины резинки, и отпускают без начальной скорости. Найдите время движения грузика вниз до точки его остановки. Начальной деформацией резинки при покоящемся грузике можно пренебречь. Какие законы Вы используете для описания движения груза на резинке? Обоснуйте их применение к данному случаю. Обоснование. Грузик движется поступательно, поэтому его можно принять за материальную точку. На первом этапе движения грузика на него действует только сила тяжести, т.к. сопротивлением воздуха мы пренебрегаем. Следовательно, на этом этапе грузик движется с ускорением свободного падения. И для описания движения тела можно применять законы прямолинейного равноускоренного движения. На втором этапе движения резинка упруго деформируется, в результате чего на грузик начинает действовать изменяющаяся по модулю и направлению сила упругости, для которой справедлив закон Гука. Таким образом, второй этап движения представляет собой механические колебания груза на резинке. Т.к. сила тяжести не меняется по модулю и направлению, то она не влияет на характер колебаний грузика. В инерциальной системе отсчета возможно применение законов колебательного движения. Перейдем к решению. 1. Введём неподвижную декартову систему координат с вертикальной осью ОХ, направленной вниз, причём начало координат поместим на уровне начального положения грузика. 2. После подъёма и отпускания грузика его движение вниз в поле силы тяжести разбивается на две стадии: вначале он свободно падает с ускорением g с высоты h до точки x = 0 (поскольку начальной деформацией резинки можно пренебречь) за время что следует из формул кинематики равноускоренного движения. 3. Затем резинка начинает растягиваться, а грузик — тормозиться вплоть до остановки в нижней точке его движения. Поскольку начальное растяжение резинки компенсирует вес грузика, то на второй стадии можно считать, что действует только упругая сила, и уравнение движения (второй закон Ньютона) в проекции на ось ОХ имеет вид: что является уравнением гармонических колебаний с периодом 4. С учётом начальных условий закон движения грузика на втором этапе представляет собой 1/4 часть периода синусоиды и происходит за время 5. Таким образом, искомое время движения грузика вниз до точки остановки равно 6. Подставляя численные данные из условия, получаем: Ответ: 1. Физические основы механики 1. Скорость течения реки v, а скорость движения лодки относительно воды v1. Определить, под каким углом относительно берега должна двигаться лодка, чтобы проплыть поперек реки. 2. Капля дождя при скорости ветра v1 падает под углом α к вертикали. Определить, при какой скорости ветра v2 капля будет падать под углом В. 4. Велосипедист проехал первую половину времени своего движения со скоростью v1, вторую половину времени – со скоростью v2. Определить среднюю скорость движения велосипедиста. 6. Студент проехал половину пути на велосипеде со скоростью v1 = 16 Далее в течение половины оставшегося времени он ехал со скоростью v2 = 12, а затем до конца пути шел пешком со скоростью v3 = 5. Определить среднюю скорость движения студента на всем пути. 21. Тело движется равноускоренно с начальной скоростью v0. Определить ускорение тела, если за время t оно прошло путь S и его скорость v. 28. Точка движется в плоскости ху из положения с координатами х1 = v1 = 0 со скоростью v = ai+ bxj(а, b— постоянные, i, j — орты осей x и y). Определите: 1) уравнение траектории точки y(x); 2) форму траектории. 29. Радиус-вектор материальной точки изменяется со временем по закону r = t 3 i+ 3t 2 j, где i, j — орты осей х и у. Определите для момента времени t = 1 с: 1) модуль скорости; 2) модуль ускорения. 30. Радиус-вектор материальной точки изменяется со временем по закону r = 4t 2 i+ 3tj + 2k. Определите: 1) скорость v; 2) ускорение а; 3) модуль скорости в момент времени t= 2 с. 31. Движение материальной точки в плоскости ху описывается законом х = At, у = At (1 + Bt), где A и B— положительные постоянные. Определите: 1) уравнение траектории материальной точки y(х); 2) радиус-вектор r точки в зависимости от времени; 3) скорость vточки в зависимости от времени; 4) ускорение а точки в зависимости от времени. 33. Линейная скорость v1 точки, находящейся на ободе вращающегося диска, в три раза больше, чем линейная скорость v2точки, находящейся на 6 см ближе к его оси. Определите радиус диска. 35. Якорь электродвигателя, имеющий частоту вращения n = 50, после выключения тока, сделав N = 628 оборотов, остановился. Определить угловое ускорение ε якоря. 37. Точка движется по окружности радиусом R = 15 см с постоянным тангенсальным ускорением aτ. К концу четвертого оборота после начала движения линейная скорость точки v1 = 15 см/с. Определить нормальное ускорение an2 точки через t 2 = 16 c после начала движения. 39. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = Аt 2 (A = 0,5 рад/с 2 ). Определить к концу второй секунды после начала движения: 1) угловую скорость диска; 2) угловое ускорение диска; 3) для точки, находящейся на расстоянии 80 см от оси вращения, тангенциальное aτ, нормальное an и полное ускорение а. 40. Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = Аt 2 (A = 0,1 рад/с 2 ). Определить полное ускорение a точки на ободе диска к концу второй секунды после начала движения, если в этот момент линейная скорость этой точки v = 0,4 м/с. 41. Диск радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением v = A*t + B*t 2 (A = 0,3 м/с 2 ; B = 0,1 м/с 3 ) Определить момент времени, для которого вектор полного ускорения а образует с радиусом колеса угол φ = 4 градуса. 42. Диск радиусом R = 10 см вращается так, что зависимость угла поворота радиуса диска от времени задается уравнением φ = A + B*t 3 (A = 2 рад; B = 4 рад/с 3 ). Определить для точек на ободе колеса: 1) нормальное ускорение a в момент времени t = 2 сек; 2) тангенсальное ускорение для этого же момента времени; 3) угол поворота φ, при котором полное ускорение составляет с радиусом колеса угол α = 45 градусов.
|