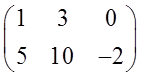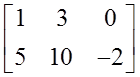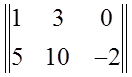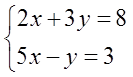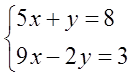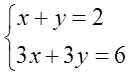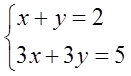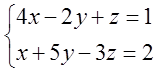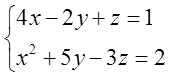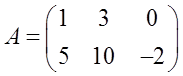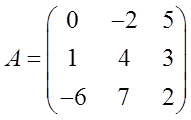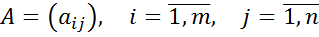Матрицы для чего они нужны

Математика для чайников. Матрицы и основные действия над ними

Определение матрицы

Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.

Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.

Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.

Операции сложения и вычитания матриц

Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.

Вычитание выполняется по аналогии, только с противоположным знаком.

Умножение матрицы на число

На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:

Операция умножения матриц

И пример с реальными числами. Умножим матрицы:

Операция транспонирования матрицы

Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:

Определитель матрицы

Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!

Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.

Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.

А если матрица три на три? Тут уже посложнее, но справиться можно.

Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

К счастью, вычислять определители матриц больших размеров на практике приходится редко.

Источник

Что такое матрица? Понятие матрицы.

Но высшая математика на то и высшая, что работает с более сложными объектами, чем привычная школьная. От этого никуда не деться.) И матрица — один из первых таких объектов, с которым студенты знакомятся уже на первом курсе ВУЗа. И мы тоже познакомимся.)

Итак, ключевые причины, почему же студенты не любят матрицы и всячески стараются избегать работы с ними. Перечислю их.

Причина первая — визуальное восприятие. Оно… непривычно, да.) С формулами, уравнениями, графиками у народа обычно всё более-менее ясно и прозрачно: в школе всё худо-бедно решалось, строилось, ощущалось. Всё знакомо. А тут… Какая-то табличка, какие-то малопонятные буковки с индексами (аж двумя!), которые так и норовят путаться перед глазами. Всё это поначалу очень смущает и даже пугает, да…

Причина вторая — это действия с матрицами. Их очень и очень много. Сложение матриц, умножение матриц, транспонирование матриц, поиск обратной матрицы, вычисление определителя, вычисление миноров матрицы, ранга матрицы… Причём все эти операции тоже весьма специфичны и имеют очень мало общего с действиями над обычными числами и алгебраическими выражениями из школьной математики. Эти фишки тоже очень здорово выбивают из колеи.

Причина третья — это рутина. Спору нет, работа с матрицами порой бывает весьма занудной. И скучной. А вместе с рутиной неизбежно возрастает и вероятность глупых арифметических ошибок, да… Особенно при работе с матрицами больших размерностей и/или в процессе элементарных преобразований. Где-то минус теряется, где-то вместо нуля единица пишется, где-то 3+4 двенадцать получается… Эти ляпы на общем фоне рутинной работы просто-напросто не замечаются. И лечатся только лишь предельным вниманием. К сожалению.

И даже после прочтения всех этих ужасов отчаиваться и впадать в панику рано. Прорвёмся!) Для начала успокою: матрица сама по себе — понятие очень простое. Да-да! И главное — полезное и очень мощное в высшей математике. Такое же полезное и мощное, как, скажем, формулы сокращённого умножения в школьной алгебре.) Сомневаетесь? Не надо.) Всё сами дальше увидите. Нужно лишь собраться с духом, рискнуть и… почитать.)

Итак, начнём с первой проблемы — с визуального восприятия.)

Что такое матрица? Устройство матрицы.

Так что же такое матрица? Нет, ничего общего с известным американским научно-фантастическим боевиком данное понятие не имеет. Ну… очень-очень отдалённое сходство всё же есть.)

Итак, удивляемся, но запоминаем:

Матрица — это просто прямоугольная таблица каких-либо элементов.

И всё! Ничего хитрого за этим страшным понятием больше не кроется.) Разумеется, каждое слово в определении несёт свой собственный смысл, да. Разберёмся?)

Слова «прямоугольная таблица» вопросов ни у кого не вызывают (надеюсь).

Например, можно сочинить что-нибудь типа такого:

Чем не прямоугольная табличка?) Но матрицы в высшей математике изображаются и выглядят немножко по-другому, нежели то что мы называем таблицей в привычном восприятии.

Чаще всего матрица в математике записывается вот так:

Всё очень просто и компактно, правда? Никаких рамок, никаких ячеек — ничего чертить и рисовать не нужно. Любая матрица записывается просто набором каких-то чисел в скобочках. Скобочки, кстати, могут быть не только круглыми. Могут быть и квадратными:

Или даже в виде вот таких двойных прямых палочек:

Это всё одно и то же. В большинстве учебников обычно используются круглые скобки. Квадратные скобки чаще встречаются в технических дисциплинах — в сопромате, строительной механике, теории упругости и т.п. Двойные — почти нигде не встречал. Я всё-таки буду следовать традициям и рисовать круглые скобки. Надеюсь, возражений нет.)

Итак, с таблицей разобрались. Что же такое «элемент»? Тоже элементарно (сорри за тавтологию). Любое число, стоящее в матрице на определённом месте, и будет её элементом! Для нашей матрицы число 1 — элемент, 5 — тоже элемент, и 10 — тоже элемент. В общем, вы поняли…

Кстати, слова «на определённом месте» я выделил не зря. И вот почему. Дело всё в том, что любую матрицу следует воспринимать именно как таблицу! А вовсе не как простое множество или набор чисел. Поясняю в чём суть. Рассматривая простое множество чисел, скажем, <1; 2; 3>, мы имеем полное право переставлять элементы множества как попало.

Например, мы можем переставить единичку и двойку. Получим:

Или переставить двойку и тройку:

И так далее. Перестановки элементов множества на его сути никак не сказываются. А вот матрицы более чувствительны к перестановкам. И переставлять элементы матрицы просто так нельзя! Каждый элемент строго на своём месте, в своей ячейке. И если переставить местами хотя бы два элемента, то получится, вообще говоря, уже другая матрица. С другими свойствами, да.

Элементами матрицы, кстати, могут быть не только числа. Могут быть и буквенные выражения, и даже функции. Всякое может быть.) Матрицы с функциями в качестве элементов так и называются — функциональными. Это — довольно сложная штука. И встречается уже в серьёзных разделах высшей математики — в дифференциальных уравнениях, в теории функций нескольких переменных и т.п. Этих ужасов пока не будет.)

Мы же пока будем работать только с матрицами, элементами которых являются числа. Или с числовыми матрицами. Намёк понятен?)

Откуда взялись матрицы, зачем они нужны и в чём их смысл?

Итак, мы выяснили, что матрица — это какая-то табличка. Чаще всего с какими-то числами. Ну и что из этого — спросите вы? Табличка и табличка… Что с ней делать-то? Просто пучить глазки? А делать можно очень много полезного! В соответствующих уроках сами увидите.)

На самом деле с матрицами вы постоянно сталкивались ещё в школе. Сами того не подозревая. Не верите? Сейчас удивитесь.)

Слова «система уравнений» вам знакомы?

Например, такая простенькая системка из двух линейных уравнений:

Решив её (например, подстановкой), получим ответ:

Или, кратенько: (1; 2).

Можно изменить коэффициенты при икс и игрек и получить какую-то новую систему. Например, такую:

Решив её, получим новый ответ: (1; 3).

А можно, например, коэффициенты при переменных не трогать, зато как-то поменять свободные члены. Вместо 8 и 3 записать, скажем, 1 и 2. Получим снова какую-то систему и какое-то решение…

Короче говоря, меняя в системе уравнений коэффициенты при неизвестных и/или свободные члены, можно получать какие-то решения для конкретной системы. Для каждого набора чисел — свои. Кстати, можно и такое наподбирать, что система вообще не будет иметь решений или будет иметь бесконечно много решений.)

Эта система имеет бесконечно много решений. И (1; 1) — решение, и (0; 2) — решение, и (0,5; 1,5) — тоже решение. Можно перечислять до посинения…)

А теперь я изменю в этой системе всего одно число и получу систему, которая вообще не имеет решений:

Кому интересно, можете решить подстановкой. Получите забавный результат 6=5. Попробуйте.)

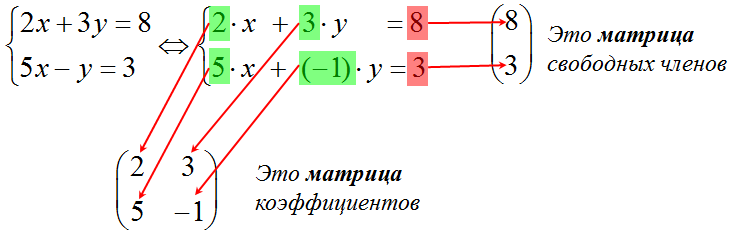
Итак, что мы видим? Мы видим, что решение системы колоссальным образом зависит от этого самого набора чисел. Причём только от него! Этот факт настолько важен, что математики даже придумали этот самый набор чисел (коэффициентов и свободных членов системы) оформлять в виде таблички. Или, говоря математическим языком, в виде матрицы.

Меняя содержимое табличек (матриц) коэффициентов и свободных членов, мы будем получать различные системы линейных уравнений. С различными решениями, да.)

Кстати, вот вам и ответ на вопрос, почему мы не можем просто так переставлять элементы в матрице. Не догадались? Да! Переставив местами хотя бы два элемента, мы получим уже другую матрицу, соответствующую другой системе уравнений. И с другими решениями…

Ну ладно, системы из двух уравнений — это ещё легко. При их решении про матрицы можно особо не вспоминать: выражай себе по-школьному икс через игрек (или наоборот), делай подстановку, решай — и дело с концом. А вот система из трёх линейных уравнений с тремя неизвестными уже гораздо злее.) Заниматься явным выражением одной переменной через другую, подстановкой и прочим школьным занудством уже неохота, да… А если уравнений и/или неизвестных ещё больше? Скажем, четыре или пять…)

И вот тут возникает вполне закономерный вопрос: а можно ли, как-то работая напрямую только с матрицами (коэффициентов и свободных членов), попробовать выяснить:

1) Есть у системы решение или нет его? Или решений вообще бесконечно много?

2) Если решение есть и единственно, то отыскать его быстро и легко.

Новость хорошая: да, можно! Добро пожаловать в новый раздел высшей математики! Под названием линейная алгебра.)

Именно этот раздел и занимается решением систем линейных алгебраических уравнений. Сокращённо — СЛАУ.) Эта страшная аббревиатура будет мозолить вам глаза на протяжении почти всех уроков этого раздела. Привыкаем.)

Причём прошу обратить особое внимание на слово «линейных». Это слово означает, что все неизвестные (x, y, z, …) входят во все уравнения максимум в первой степени и нигде не должно быть деления на неизвестное.

Это система двух линейных алгебраических уравнений (СЛАУ) с тремя неизвестными. Все неизвестные (x, y, z) в только первой степени, деления на неизвестное ни в одном из уравнений нету. То что число неизвестных больше числа уравнений — вопрос другой. В соответствующем уроке мы научимся с такими злыми системами расправляться.) Главное, что оба уравнения — линейные. Это важно.)

А теперь я изменю в этой системе всего одно слагаемое. Нарисую, например, квадратик над иксом во втором уравнении:

А вот такая система уравнений будет уже нелинейна, да… Именно из-за этого самого квадратика, нарушающего базовый принцип «все неизвестные только в первой степени». К нелинейным системам имеется свой индивидуальный подход, и линейная алгебра перед ними бессильна… С такими системами мы в этом разделе работать не будем. На радость студентам.)

Матрицы — очень мощный инструмент для решения систем линейных алгебраических уравнений (СЛАУ).

Но не одними лишь системами уравнений ограничивается применение матриц! Матрица — это ещё и своего рода математический оператор. Или преобразователь. Который что-то куда-то преобразует. Или отображает. Как фотоаппарат.) Скажем, один вектор через матрицу можно отобразить в другой. Мощная штука.) Об этом в более серьёзных темах линейной алгебры будет. А системы — так, частный случай. Для начального знакомства.

Как обозначать матрицу и её элементы?

Очень просто. Любые матрицы в математике обозначаются большими буквами латинского алфавита: A, B, C и так далее.

Например, нашу матрицу, приведённую в начале урока, можно обозначить вот так:

И все дела. Слева от знака равенства — название матрицы, справа — её содержимое. В скобочках.)

Но это ещё не все обозначения. Есть и другие, более специфические. Разберём и их.

Любая матрица — это ведь табличка, не так ли? А из чего у нас состоит любая табличка? Правильно, из строчек и колонок! Только это в обиходе.) А в математике те же самые названия звучат более научно — строки и столбцы! Зацените.)

Количество этих самых строк и столбцов коротко записывают в виде произведения m x n и называют размерностью матрицы. Которая дополнительно может указывается в виде подстрочного знака.

Читается эта запись очень просто: «матрица A размерности m на n». И вот тут студентов могут подстерегать первые проблемы. Какое число (буква) за что отвечает?

Запоминаем:

В размерности матрицы m x n первое число (m) — это (всегда!) количество СТРОК в матрице. Второе число (n) — количество СТОЛБЦОВ.

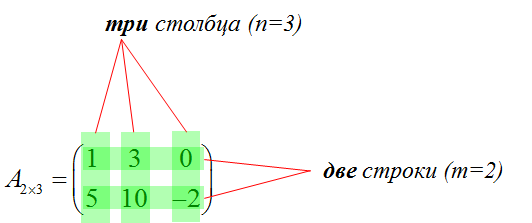
Именно в таком порядке. Сначала строки, а потом — столбцы. А не наоборот. Например, наша матрица — это матрица размера «два на три»:

У неё две строки (m=2) и три столбца (n=3).

Размерность — ключевая характеристика любой матрицы. Почему? А потому, что на некоторые операции с матрицами (например, на сложение, умножение, взятие определителя и обратной матрицы) существуют очень жёсткие ограничения по размерности! Сами увидите. В соответствующих уроках.)

А как кратко в общем виде обозначать элементы матрицы? Тоже просто. Маленькими латинскими буквами с двойным индексом.

И всё. Читается эта закорючка так: «а и-жи». Или: «а итое-житое». Забавно, да? Тем не менее вполне себе научно.)

И снова могут быть проблемы с расшифровкой индексов. В школе ведь мы привыкли работать с одиночными индексами. В прогрессиях, например. А тут — двойной! Какой индекс что означает? Не беда! Принцип расшифровки индексов тот же самый — сначала строка, а потом столбец. Первый индекс «i» («и»)– это номер строки, где находится интересующий нас элемент. Второй индекс «j« («жи») – номер столбца.

Например, нам дана такая матрица A:

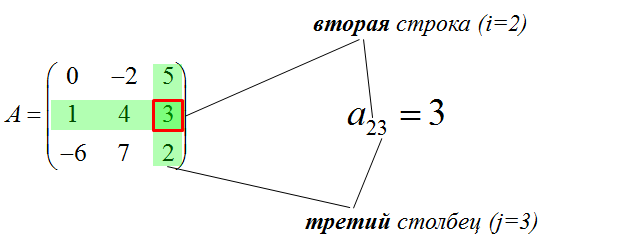
Здесь первый индекс «и» равен двойке (i=2), а второй индекс «жи» – тройке (j=3). Вот и пересекаем (мысленно!) вторую строку и третий столбец. На пересечении получаем нужный нам элемент a₂₃ = 3.

Точно так же на пересечении первой строки и первого столбца мы получим элемент матрицы a₁₁ = 0, на пересечении третьей строки и второго столбца — элемент a₃₂ = 7 и так далее. Чем-то похоже на игру в кораблики или морской бой, не находите?) Вроде бы, всё элементарно. И что, думаете не ошибаются люди? Ошибаются, ещё как! Ещё один источник дурацких ошибок при работе с элементами матриц — это неправильная нумерация строк и столбцов. Со столбцами обычно всё ясно — нумеруем и читаем привычно, слева направо. Не арабы, чай…) А вот со строками могут случаться и непонятки — сверху вниз их нумеровать или снизу вверх…

Запоминаем:

В элементе матрицы a_ij первый индекс (i) — номер строки, второй индекс (j) — номер столбца. Нумерация строк (всегда!) — сверху вниз. Нумерация столбцов (всегда!) — слева направо.

А теперь, разобравшись с загадочными индексами i и j, мы подходим к самому научному способу задания матрицы — через элемент матрицы в общем виде и диапазон изменения индексов.

Вот она, эта запись:

Расшифровываются эти страшные иероглифы так:

Задана матрица А с элементами a_ij , где индекс «i» принимает все натуральные значения от единицы до «эм» включительно, а индекс «j» — все натуральные значения от единицы до «эн» включительно.

Солидно, да… Куда проще не заморачиваться и написать кратко и точно A_mxn, правда? Но будьте готовы и к такой супернаучной форме записи. Особенно в каких-нибудь продвинутых учебниках.)

Внимание! Запись элемента a₂₃ читается и произносится как «а два три«. Именно так, вы не ослышались.) Ни в коем случае не «a двадцать три«! Или b₁₁ — это элемент «бэ один один« (а не «бэ одиннадцать« )! Такое чтение — это… гм… серьёзный вызов преподавателю.) И говорит о полном отсутствии хоть какого-то понимания. О «зачёте» (или «удовл») даже и не мечтайте после этого. Вот так.

Источник

От действий над матрицами к пониманию их сути…

Очень уважаю людей, которые имеют смелость заявить, что они что-то не понимают. Сам такой. То, что не понимаю, — обязательно должен изучить, осмыслить, понять. Статья «Математика на пальцах», и особенно матричная запись формул, заставили меня поделиться своим небольшим, но, кажется, немаловажным опытом работы с матрицами.

Лет эдак 20 назад довелось мне изучать высшую математику в вузе, и начинали мы с матриц (пожалуй, как и все студенты того времени). Почему-то считается, что матрицы — самая лёгкая тема в курсе высшей математики. Возможно — потому, что все действия с матрицами сводятся к знанию способов расчёта определителя и нескольких формул, построенных — опять же, на определителе. Казалось бы, всё просто. Но… Попробуйте ответить на элементарный вопрос — что такое определитель, что означает число, которое вы получаете при его расчёте? (подсказка: вариант типа «определитель — это число, которое находится по определённым правилам» не является правильным ответом, поскольку говорит о методе получения, а не о самой сути определителя). Сдаётесь? — тогда читаем дальше.

Сразу хочу сказать, что я не математик ни по образованию, ни по должности. Разве что мне интересна суть вещей, и я порой пытаюсь до них «докопаться». Так же было и с определителем: нужно было разобраться со множественной регрессией, а в этом разделе эконометрики практически всё делается через… матрицы, будь они неладны. Вот и пришлось мне самому провести небольшое исследование, поскольку ни один из знакомых математиков не дал внятного ответа на поставленный вопрос, изначально звучавший как «что такое определитель». Все утверждали, что определитель — это такое число, которое особым образом посчитано, и если оно равно нулю, то… В общем, как в любом учебнике по линейной алгебре. Спасибо, проходили.

Если какую-то идею придумал один человек, то другой человек должен быть в состоянии её понять (правда, для этого порой приходится вооружаться дополнительными знаниями). Обращение к «великому и могучему» поисковику показало, что «площадь параллелограмма равна модулю определителя матрицы, образованной векторами — сторонами параллелограмма». Говоря простым языком, если матрица — это способ записи системы уравнений, то каждое уравнение в отдельности описывает вектор. Построив из точки начала координат векторы, заданные в матрице, мы таким образом зададим в пространстве некоторую фигуру. Если наше пространство одномерное, то фигура — это отрезок; если двумерное — то фигура — параллелограмм, и так далее.

Получается, что для одномерного пространства определитель — это длина отрезка, для плоскости — площадь фигуры, для трёхмерной фигуры — её объём… дальше идут n-мерные пространства, вообразить которые нам не дано. Если объём фигуры (то есть определитель для матрицы 3*3) равен нулю, то это означает, что сама фигура не является трёхмерной (она может быть при этом двухмерной, одномерной или вообще представлять собой точку). Ранг матрицы — это истинная (максимальная) размерность пространства, для которого определитель не равен нулю.

Так, с определителем почти всё понятно: он определяет «объёмность» фигуры, образованной описанными системой уравнений векторами (хотя непонятно, почему его значение не зависит от того, имеем мы дело с исходной матрицей, или с транспонированной — возможно, транспонирование — это вид аффинного преобразования?). Теперь нужно разобраться с действиями над матрицами…

Если матрица — это система уравнений (а иначе зачем нам таблица каких-то цифр, не имеющих к реальности никакого отношения?), то мы можем с ней делать разные вещи. Например, можем сложить две строки одной и той же матрицы, или умножить строку на число (то есть каждый коэффициент строки умножаем на одно и то же число). Если у нас есть две матрицы с одинаковыми размерностями, то мы их можем сложить (главное, чтобы при этом мы не сложили бульдога с носорогом — но разве математики, разрабатывая теорию матриц, думали о таком варианте развития событий?). Интуитивно понятно, тем более что в линейной алгебре иллюстрациями подобных операций являются системы уравнений.

Однако в чём смысл умножения матриц? Как я могу умножить одну систему уравнений на другую? Какой смысл будет иметь то, что я получу в этом случае? Почему для умножения матриц неприменимо переместительное правило (то есть произведение матриц В*А не то что не равно произведению А*В, но и не всегда осуществимо)? Почему, если мы перемножим матрицу на вектор-столбец, то получим вектор-столбец, а если перемножим вектор-строку на матрицу, то получим вектор-строку?

Ну, тут уж не то что Википедия, — тут даже современные учебники по линейной алгебре бессильны дать какое-либо внятное объяснение. Поскольку изучение чего-либо по принципу «вы сначала поверьте — а поймёте потом» — не для меня, копаю в глубь веков (точнее — читаю учебники первой половины XX века) и нахожу интересную фразу…

Если совокупность обычных векторов, т.е. направленных геометрических отрезков, является трёхмерным пространством, то часть этого пространства, состоящая из векторов, параллельных некоторой плоскости, является двумерным пространством, а все векторы, параллельные некоторой прямой, образуют одномерное векторное пространство.

В книгах об этом напрямую не говорится, но получается, что векторам, параллельным некоторой плоскости, необязательно лежать на этой плоскости. То есть они могут находиться в трёхмерном пространстве где угодно, но если они параллельны именно этой плоскости, то они образуют двумерное пространство… Из приходящих мне на ум аналогий — фотография: трёхмерный мир представлен на плоскости, при этом вектору, параллельному матрице (или плёнке) фотоаппарата, будет соответствовать такой же вектор на картинке (при условии соблюдении масштаба 1:1). Отображение трёхмерного мира на плоскости «убирает» одно измерение («глубину» картинки). Если я правильно понял сложные математические концепции, перемножение двух матриц как раз и представляет собой подобное отражение одного пространства в другом. Поэтому, если отражение пространства А в пространстве В возможно, то допустимость отражения пространства В в пространстве А — не гарантируется.

Любая статья заканчивается в тот момент, когда автору надоедает её писать. Поскольку я не ставил перед собой цели объять необъятное, а исключительно хотел понять суть описанных операций над матрицами и то, как именно матрицы связаны с решаемыми мной системами уравнений, я не полез в дальнейшие дебри линейной алгебры, а вернулся к эконометрике и множественной регрессии, но сделал это уже более осознанно. Понимая, что и зачем я делаю и почему только так, а не иначе. То, что у меня получилось в этом материале, можно озаглавить как «глава о сути основных операций линейной алгебры, которую почему-то забыли напечатать в учебниках». Но ведь мы же не читаем учебников, правда? Если честно, когда я учился в университете, мне очень не хватало именно понимания затронутых здесь вопросов, поэтому я надеюсь, что, изложив этот непростой материал по возможности простыми словами, я делаю доброе дело и помогаю кому-то вникнуть в саму суть матричной алгебры, переведя операции над матрицами из раздела «камлание с бубном» в раздел «практические инструменты, применяемые осознанно».

Источник