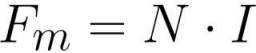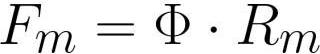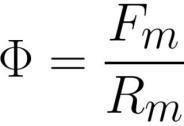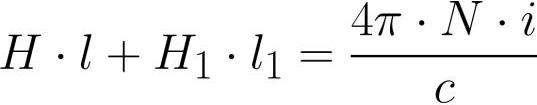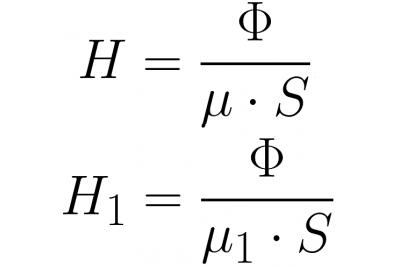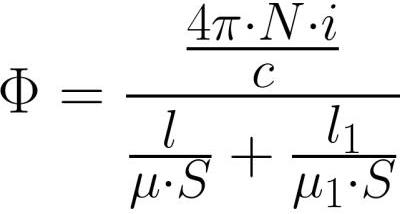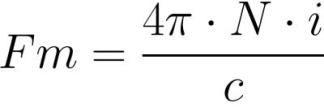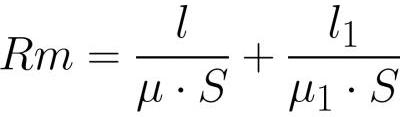Что такое магнитодвижущая сила, закон Гопкинсона

Во второй половине XIX века, английский физик Джон Гопкинсон и его брат Эдвард Гопкинсон, разрабатывая общую теорию магнитных цепей, вывели математическую формулу, получившую название «формула Гопкинсонов» или закон Гопкинсона, являющийся аналогом закона Ома (применяемого для расчета электрических цепей).

Так, если классический закон Ома математически описывает связь между током и электродвижущей силой (ЭДС), то закон Гопкинсона аналогичным образом выражает связь между магнитным потоком и так называемой магнитодвижущей силой (МДС).

В результате оказалось, что магнитодвижущая сила — это физическая величина, характеризующая способность электрических токов создавать магнитные потоки. И закон Гопкинсона, в связи с этим, может успешно использоваться в расчетах магнитных цепей, так как МДС в магнитных цепях является аналогом ЭДС в электрических цепях. Датой открытия закона Гопкинсона считается 1886 год.

Величина магнитодвижущей силы (МДС) изначально измеряется в амперах, либо, если речь идет о катушке с током или об электромагните, то для удобства расчетов пользуются ее выражением в ампер-витках:

где: Fm — магнитодвижущая сила в катушке [ампер*виток], N – количество витков в катушке [виток], I – величина тока в каждом из витков катушки [ампер].

Если сюда ввести значение магнитного потока, то Закон Гопкинсона для магнитной цепи примет вид:

где: Fm — магнитодвижущая сила в катушке [ампер*виток], Ф — магнитный поток [вебер] или [генри*ампер], Rm – магнитное сопротивление проводника магнитного потока [ампер*виток/вебер] или [виток/генри].

Текстовая формулировка закона Гопкинсона изначально такова: «в неразветвленной магнитной цепи магнитный поток прямо пропорционален магнитодвижущей силе и обратно пропорционален полному магнитному сопротивлению». То есть данный закон определяет связь между магнитодвижущей силой, магнитным сопротивлением и магнитным потоком в цепи:

здесь: Ф — магнитный поток [вебер] или [генри*ампер], Fm — магнитодвижущая сила в катушке [ампер*виток], Rm – магнитное сопротивление проводника магнитного потока [ампер*виток/вебер] или [виток/генри].

Здесь важно отметить, что фактически магнитодвижущая сила (МДС) имеет принципиальное отличие от электродвижущей силы (ЭДС), которое заключается в том, что непосредственно в магнитном потоке никакие частицы не движутся, тогда как ток, возникающий под действием ЭДС, предполагает движение заряженных частиц, например электронов в металлических проводниках. Однако представление о МДС помогает решать задачи расчета магнитных цепей.

Рассмотрим, например, неразветвленную магнитную цепь, в которую входит ярмо площадью поперечного сечения S, одинаковой по всей длине, при этом материал ярма имеет магнитную проницаемость мю.

Поскольку магнитный поток внутри ярма и внутри зазора имеет одну и ту же величину (в силу непрерывности линий магнитной индукции), то расписав Ф = BS и B=мю*H, распишем напряженности магнитного поля более подробно, а затем подставим в вышеприведенную формулу:

Легко видеть, что подобно ЭДС в законе Ома для электрических цепей, МДС

играет здесь как-бы роль электродвижущей силы, а магнитное сопротивление

роль сопротивления (по аналогии с классическим Законом Ома).

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Ток или поток? Магнитные цепи и их основные характеристики

Привет, Хабр! С недавнего времени я стал задумываться об актуальности статей и заметил, что на Хабре нет ни одной обзорной статьи про магнитные цепи. Как так!? Ведь это. а что это такое?

Действительно, наверняка даже самые отстраненные от инженерного дела люди имеют представление о том, что такое электрические цепи, но возможно, что про магнитные цепи не слышали вовсе. Каждый школьник когда-то в учебнике физики наблюдал разные схемы и формулы, описывающие законы Ома. Но магнитные цепи в рамки школьного курса не входят.

Я решил написать данную статью, чтобы показать, насколько удивителен мир физики и заинтересовать школьников в её изучении. В данной статье, однозначно, для полноты вещей будут и выводы формул и использование некоторых математических операций, которые могут быть известны не всем, но такие моменты я постараюсь сгладить. Приступим!

Что нужно вспомнить?

Применение магнитных цепей

Магнитные цепи находят очень большое поле применения, а именно, они используются для надежного пропускания магнитного потока по специальному проводнику с минимальными или, в некоторых случаях, определенными потерями. В электротехнической промышленности широко используется взаимная зависимость магнитной и электрической энергий, переход из одного состояния в другое. На подобном принципе работают, например, трансформаторы, разные электродвигатели, генераторы и другие устройства.

Как устроены магнитные цепи?

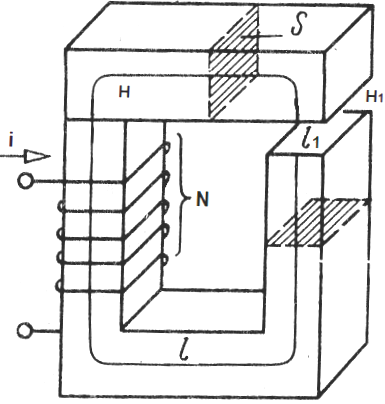
Магнитную цепь, на самом деле, не так сложно представить, как может показаться человеку, который о них впервые слышит. Обычно магнитные цепи представляют из себя некоторые фигуры из ферромагнитного сердечника с источником или несколькими источниками ПОтока. Пожалуй, один из самых простых примеров с одним источником, который можно взять на вооружение, проиллюстрирован ниже:

Перед продолжением обусловимся, что среди электротехников сердечник называют магнитопроводом. Часть магнитопровода, на которой отсутствуют обмотки и которая служит для замыкания магнитной цепи, называется «ярмо».

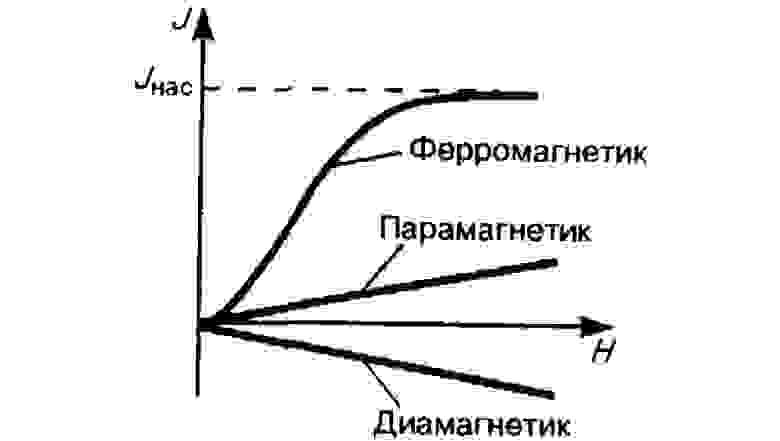
Вспомним теперь про ферромагнитные материалы. Почему именно они? Дело в том, что благодаря высокому значению магнитной проницаемости, что сигнализирует о хорошей намагниченности ферромагнетика, силовые линии магнитного поля практически не выходят за пределы сердечника, либо не выходят вовсе. Однако это будет справедливо лишь тогда, когда наш сердечник замкнутый, либо имеет небольшие зазоры. То есть, ферромагнетики обладают сильно выраженными магнитными свойствами, когда как у парамагнетиков и диамагнетиков они значительно слабее, что можно наблюдать на следующем графике зависимости намагниченности от напряженности магнитного поля:

Вещества, которые входят в конструкцию магнитопровода, могут обладать не только сильномагнитными свойствами, но также и слабомагнитными. Однако мы рассматриваем сердечник из ферромагнитного материала.

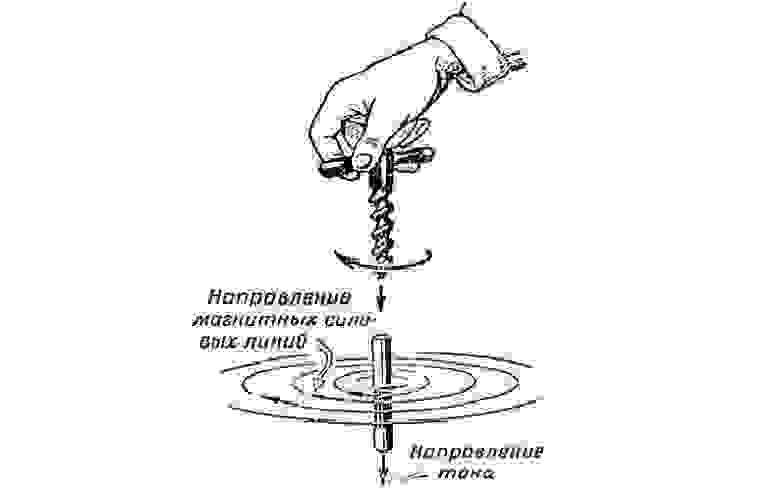
Ещё из школьного курса мы представляем себе картину с линиями магнитной индукции соленоида, мы можем визуально представить его поле и понимаем, что концентрация силовых линий, их насыщенность, наибольшая в центре рассматриваемого соленоида. Тут очень важно вспомнить правило буравчика, чтобы правильно указать направление силовых линий.

Отсюда становится ясно, что катушки-источники порождают магнитное поле, а следовательно и поток линий магнитной индукции. Такие линии будут циркулировать по нашему сердечнику, словно повторяя его форму. Именно поэтому нам важно условие замкнутости сердечника и материал, из которого он сделан. Положим, что наш воображаемый сердечник замкнут. Из этого следует, что и силовые линии замкнуты, а следовательно выполняется теорема Гаусса для магнитного поля, которая гласит: поток линий магнитной индукции через замкнутую поверхность равен нулю. Стоит учесть, что поток адаптируется под площадь сечения.*

Ну и в конечном счете ферромагнитный сердечник поток куда-то передает! Аналогичным образом замкнутый проводник позволяет передать электрический ток.

Отлично! Мы разобрались с тем, что такое магнитные цепи и даже вспомнили про теорему Гаусса и ферромагнетики. Теперь поговорим о том, какие следствия вытекают из теоремы Гаусса и возможности пренебрежения полем вне сердечника и в зазорах.

1] Магнитные потоки Ф₁ и Ф₂ через произвольные сечения будут равны между собой.

2] В узле (разветвлении) сердечника алгебраическая сумма потоков (с учетом их направлений) будет равна нулю. Мне одному это что-то напоминает?

Расчет магнитных цепей

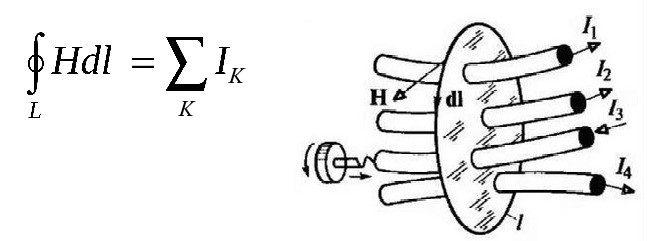
Криволинейный интеграл по замкнутому контуру от напряженности магнитного поля будет равен алгебраической сумме токов, сцепленных (окруженных) данным контуром.

Также мы помним, что напряженность магнитного поля связана с магнитным потоком следующим образом:

Руководствуясь приведенным законом полного тока и определением напряженности через магнитный поток, мы можем переписать закон полного тока относительно магнитного потока.

Откуда в уравнении появился и что символизирует аргумент l? Все просто. Так как мы рассматриваем контур L, то логично предположить, что на разных его участках наши показатели могут принимать разные значения: площадь сечения может изменяться, как и магнитная проницаемость или магнитный поток.

Полученное уравнение можно рассматривать как второй закон Кирхгофа, который, напомню, звучит следующим образом:

В любой момент времени алгебраическая сумма напряжений на ветвях контура равна нулю.

Для полной ясности, проведем аналогию между электрическими и магнитными цепями, а также их величинами.

Именно проведя аналогичное представление для электрической цепи, мы можем рассчитывать магнитные цепи. Для того, чтобы это сделать, следует:

Мысленно разбить сердечник на отдельные однородные участки (непрерывные, с постоянным сечением) без разветвлений и определить их магнитные сопротивления;

Построить эквивалентную электрическую цепь, последовательно заменяя участки магнитной цепи участками электрической с электрическими сопротивлениями, а также заменяя индуктивности (катушки) на источники ЭДС;

После обозначения заданных сопротивлений и ЭДС, можем вычислить в общем токи в элементах электрической цепи;

Произвести замену полученных величин согласно таблице (токи в потоки, ЭДС в МДС [Магнитодвижущую силу / Ампер-витки], а электрическое сопротивление в магнитное сопротивление).

Именно таким образом, мы можем рассчитать характеристики магнитной цепи. Полученные результаты позволяют, например, вычислить индуктивности.

А примеры расчетов будут?

Заключение

Во-вторых, вернемся к началу статьи. Там я задался целью показать, почему физика удивительна. Не хочу быть многословным, поэтому просто попрошу вспомнить все то, что было описано выше. Мы оперировали моделями, которые относятся к разделу физики электричества и перенесли их на физику магнетизма. Наверняка, вы замечали, насколько часто встречаются элементы механики в иных разделах. Это по истине удивительно! Однако главное не поработиться иллюзией, что в мире все законы нам предельно известны.

Источник

Магнитодвижущая сила

Магнитодвижущая сила (МДС) — физическая величина, характеризующая работу непотенциальных сил, порождающих магнитный поток в магнитных цепях; аналог ЭДС в электрических цепях. Величина измеряется в амперах (СИ) или же в гилбертах (СГС), причём 1А = = 1.257 Гб.

Магнитодвижущая сила в индукторе или электромагните вычисляется по формуле:

где ω — количество витков в обмотке, I — ток в проводнике.

Выражение для магнитного потока в магнитной цепи, также известное как закон Хопкинса, имеет следующий вид:

где Φ — величина магнитного потока, Rm — магнитное сопротивление проводника. Данная запись является аналогом закона Ома в электрических цепях.

Литература

Топологические объектыЛиния Блоха · Точка БлохаПриборыЭлектромагнит · СКВИД · Датчик Холла · Магнитная лента · Жёсткий диск · MRAM · Магнитная ловушка · ЯМР-томографУчёныеМайкл Фарадей · Андре Мари Ампер · Пьер Кюри · Пьер Вейс · Феликс Блох · Луи Неель · Эдвин ХоллДругоеСпинтроника

Полезное

Смотреть что такое «Магнитодвижущая сила» в других словарях:

МАГНИТОДВИЖУЩАЯ СИЛА — (намагничивающая сила), величина, характеризующая магн. действие электрич. тока. Вводится для магнитных цепей по аналогии с электродвижущей силой в электрич. цепях. М. с. F равна циркуляции вектора напряжённости магн. поля Н по замкнутому контуру … Физическая энциклопедия

магнитодвижущая сила — Скалярная величина, равная линейному интегралу напряженности магнитного поля вдоль рассматриваемого контура и равная полному току, охватываемому этим контуром. [ГОСТ Р 52002 2003] Тематики электротехника, основные понятия Синонимы магнитодвижущая … Справочник технического переводчика

МАГНИТОДВИЖУЩАЯ СИЛА — (МДС), млн. намагничивающая сила, характеристика, определяющая магнитный поток (см. (8)) в данной магнитной цепи (см. (17)) и играющая в ней такую же роль, как электродвижущая сила (ЭДС) в цепи электрического тока. Единица магнитодвижущей силы в… … Большая политехническая энциклопедия

МАГНИТОДВИЖУЩАЯ СИЛА — (мдс) (намагничивающая сила) характеристика способности источников магнитного поля (электрических токов) создавать магнитные потоки; вводится при расчетах магнитных цепей по аналогии с эдс электрических цепей … Большой Энциклопедический словарь

магнитодвижущая сила — (намагничивающая сила), характеристика способности источников магнитного поля (электрических токов) создавать магнитные потоки; вводится при расчётах магнитных цепей по аналогии с эдс электрических цепей. * * * МАГНИТОДВИЖУЩАЯ СИЛА… … Энциклопедический словарь

магнитодвижущая сила — magnetovara statusas T sritis automatika atitikmenys: angl. magnetomotive force vok. Durchflutung, f; magnetomotorische Kraft, f rus. магнитодвижущая сила, f pranc. force magnétomotrice, f … Automatikos terminų žodynas

магнитодвижущая сила — magnetovara statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. magnetomotive force vok. magnetomotrische Kraft, f rus. магнитодвижущая сила, f pranc. force… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

магнитодвижущая сила — magnetovara statusas T sritis fizika atitikmenys: angl. magnetomotive force vok. magnetomotorische Kraft, f rus. магнитодвижущая сила, f pranc. force magnétomotrice, f … Fizikos terminų žodynas

Магнитодвижущая сила — намагничивающая сила, величина, характеризующая магнитное действие электрического тока. Вводится при расчётах магнитных цепей (См. Магнитная цепь) по аналогии с электродвижущей силой (См. Электродвижущая сила) в электрических цепях. М. с … Большая советская энциклопедия

МАГНИТОДВИЖУЩАЯ СИЛА — (намагничивающая сила), физ. величина, характеризующая способность источников магн. поля (электрич. токов) создавать магн. потоки. Вводится при расчётах магн. цепей по аналогии с эдс электрич. цепей. Единица СИ ампер … Естествознание. Энциклопедический словарь

Источник