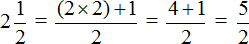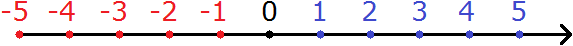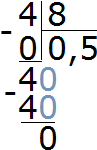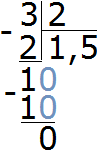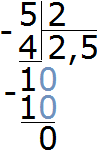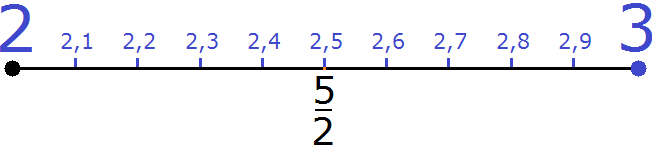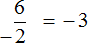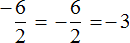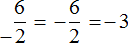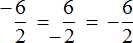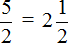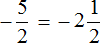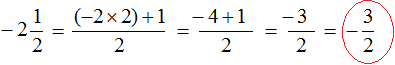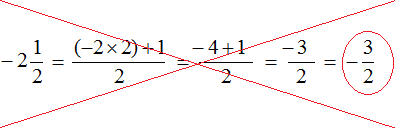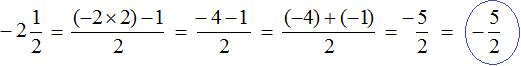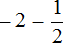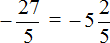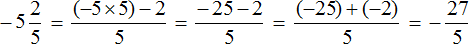Множество рациональных чисел это что
Что такое рациональные числа?
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение рациональных чисел
Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Если число можно получить делением двух целых чисел, то это число рациональное.
Рациональные числа — это те, которые можно представить в виде
где числитель m — целое число, а знаменатель n — натуральное число.
Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Множество рациональных чисел принято обозначать латинской буквой Q.
Примеры рациональных чисел:
Свойства рациональных чисел
У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.
Кроме основных перечисленных есть еще ряд свойств:
Мы знаем, что 0 = d + (-d) для любого рационального d, значит a * 0 = a * (d + (-d)).
Распределительный закон позволяет переписать выражение:
Так получилась сумма двух противоположных чисел, которая в результате дает нуль, что доказывает равенство a * 0 = 0.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Определение иррационального числа
Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.
Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.
Обозначение множества иррациональных чисел: латинская буква I.
Действительные или вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.
Свойства иррациональных чисел:
Различие между целыми, натуральными и рациональными числами
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое: один банан, две тетрадки, десять стульев.
А вот, что точно не является натуральным числом:
Целые числа — это натуральные числа, противоположные им и нуль.
Какие числа называются рациональными мы уже знаем из первой части статьи. Повторим еще раз.
Рациональные числа — это конечные дроби и бесконечные периодические дроби.
Например:
Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель — натуральным. Поэтому во множество рациональных чисел входит множество целых и натуральных чисел.
Но не все числа можно назвать рациональными. Например, бесконечные непериодические дроби не принадлежат множеству рациональных чисел. Так √3 или 𝜋 (число пи) нельзя назвать рациональными числами.
Рациональные числа: определения, примеры
Данная статья посвящена изучению темы «Рациональные числа». Ниже приведены определения рациональных чисел, даны примеры, рассказано о том, как определить, является ли число рациональным, или нет.
Рациональные числа. Определения
Прежде чем дать дефиницию рациональных чисел вспомним, какие еще есть множества чисел, и как они связаны между собой.
Натуральные числа, в совокупности с противоположными им и числом ноль образуют множество целых чисел. В свою очередь, совокупность целых дробных чисел образует множество рациональных чисел.
Определение 1. Рациональные числа
Таким образом, можно оставить ряд свойств рациональных чисел:
Приведенное выше определение рациональных чисел можно сформулировать более кратко. Еще раз ответим на вопрос, что такое рациональное число.
Определение 2. Рациональные числа
Можно показать, что данное определение равносильно предыдущему определению рациональных чисел. Чтобы сделать это, вспомним, что черта дроби равносильна знаку деления. С учетом правил и свойств деления целых чисел, можно записать следующие справедливые неравенства:
Таким образом, можно записать:
Приведем еще одну эквивалентную форму определения рациональных чисел.
Определение 3. Рациональные числа
Данное определение напрямую следует из самого первого определения этого пункта.
Подведем итог и сформулируем резюме по данному пункту:
Какое из чисел является рациональным?
Как мы уже выяснили, любое натуральное число, целое число, правильная и неправильная обыкновенная дробь, периодическая и конечная десятичная дробь являются рациональными числами. Вооружившись этими знаниями можно без труда определить, является ли какое-то число рациональным.
Однако на практике часто приходится иметь дело не с числами, а с числовыми выражениями, которые содержат корни, степени и логарифмы. В некоторых случаях ответ на вопрос «рационально ли число?» является далеко не очевидным. Рассмотрим методы ответа на этот вопрос.
Таким образом, упрощение сложного числового выражения позволяет определить, рационально ли заданное им число.
Теперь разберемся со знаком корня.
5 = 2 log 2 5 = 2 m n 5 n = 2 m
Очевидно, последнее равенство невозможно так как в левой и правой частях находятся соответственно нечетное и четное числа. Следовательно, сделанное предположение неверно, и число log 2 5 не является рациональным числом.
Что такое Рациональные числа
Определение рациональных чисел
Рациональное число — это число, которое можно представить как дробь. Т.е. если число можно получить делением двух целых чисел (число без дробной части), то это число рациональное.
Это число, которое можно представить обыкновенной дробью 
Множество рациональных чисел обозначается буквой “Q”.
Слово «рациональный» произошло от латыни «ratio», которое имеет несколько значений — число, расчёт, нумерация, рассуждение, разум и др.
Свойства рациональных чисел
Допустим а, b и c — любые рациональные числа.
Переместительные и сочетательные законы
а + b = b + а, например: 2 + 3 = 3 + 2;
а + (b + с) = (а + b) + с, например: 2 + (3 + 4) = (2 + 3) + 4;
а + 0 = а, например: 2 + 0 = 2;
а + (– а) = 0, например: 2 + (– 2) = 0
Переместительные и сочетательные законы при умножении
a × b = b × a, например: 2 × 3 = 3 × 2
a × (b × c) = (a × b) × c, например: 2 × (3 × 4) = (2 × 3) × 4
а × 1 = а, например: 2 × 1 = 2
а × 1/a = 1, если а ≠ 0; например: 2 × 1/2 = 1
а × 0 = 0, например: 2 × 0 = 0
а × b = 0, значит: или а = 0, или b = 0, или оба равны нулю
Распределительный закон умножения
(а + b) × с = ас + bс например: (2 + 3) × 4 = 2×4 + 3×4
(а – b) × с = ас – bс например: (3 – 2) × 4 = 3×4 – 2×4
Иррациональные числа
Иррациональные числа — противоположность рациональным числам, это те, которые НЕ могут быть записаны как простая дробь.
Множество иррациональных чисел обозначается буквой “I”.
Какая разница между целыми, натуральными и рациональными числами
Целые числа — это натуральные числа, противоположные им числа (ниже нуля) и нуль.
Все целые числа являются рациональными числами (натуральные в том числе), т. к. их можно представить в виде обыкновенной дроби.
Множество целых чисел в математике обозначается буквой Z.
Натуральные числа
Натуральные числа — это только целые числа, начиная с 1.
Этот счёт появился натуральным способом, когда люди ещё считали на пальцах и не знали цифр («у меня столько коз, сколько пальцев на обеих руках»), поэтому нуль не входит в натуральные числа.
Множество натуральных чисел в математике обозначается буквой N.
Все десятичные дроби рациональные числа?
Десятичные дроби выглядят таким образом:
Это обычные дроби, у которых знаменатель равен 10, 100, 1000 и т. д. Наши примеры мы можем записать в таком виде:
3,4 =  ;
;
2,19 =  ;
;
0,561 =  .
.
Это означает, что любая конечная десятичная дробь является рациональным числом.
Любую периодическую дробь тоже можно представить в виде обыкновенной дроби:

Следовательно, любая периодическая дробь является рациональным числом.
Но БЕСКОНЕЧНЫЕ и НЕПЕРИОДИЧЕСКИЕ десятичные дроби не считаются рациональными числами, т. к. их нельзя показать в виде обыкновенной дроби.
Можно запомнить, как шпаргалку, что число Пи (3,14159. ) иррациональное. У него очень много неповторяющихся знаков после запятой и его невозможно представить в виде обыкновенной дроби.
Корни — рациональные числа или иррациональные?
Подавляющая часть квадратных и кубических корней — иррациональные числа. Но бывают исключения: если его можно представить как дробь (по определению рационального числа). Например:
История рациональных чисел и дробей
Самое раннее известное упоминание иррациональных чисел было между 800 и 500 г. до н. э. в индийской Сулба-Сутре.
Первое доказательство существования иррациональных чисел принадлежит древнегреческому философу-пифагорейцу Гиппасу из Метапонта. Он доказал (вероятнее всего геометрически) иррациональность квадратного корня из 2.
Легенда гласит, что Гиппас из Метапонта открыл иррациональные числа когда попытался представить квадратный корень из 2 в виде дроби. Однако Пифагор верил в абсолютность чисел и не смог принять существование иррациональных чисел.
Считается, что из-за этого между ними получился конфликт, который породил множество легенд. Многие говорят о том, что как раз это открытие убило Гиппаса.
В вавилонских записях по математике часто можно увидеть шестидесятеричную систему счисления, в которой уже использовались дроби. Эти записи были сделаны более 4000 лет назад, система была немного не такой, как у нас, но смысл тот же.
У египтян, которые жили в более поздний период, также был свой способ записи дробей, что-то похожее на: 3⁻¹ или 5⁻¹.
Рациональные числа, понятие и примеры.
Рациональные числа вы с ними уже знакомы, осталось только обобщить и сформулировать правила. Так какие числа называются рациональными числами? Рассмотрим подробно в этой теме урока.
Понятие рациональных чисел.
Определение:
Рациональные числа – это числа, которые можно представить в виде дроби \(\frac
Другими словами, можно сказать:
Рациональные числа – это все натуральные числа, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Разберем каждый пункт подробно.
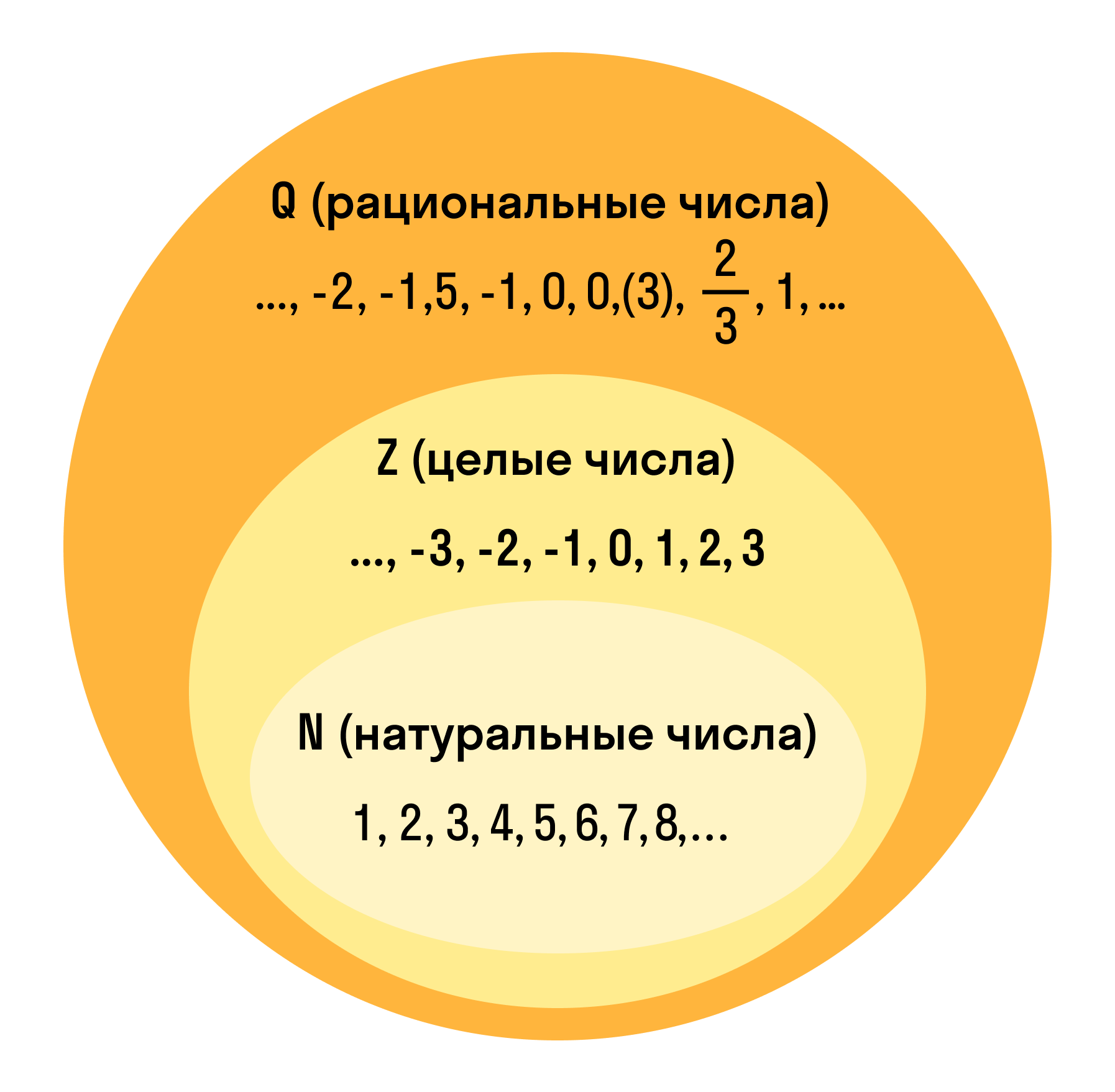
Множество рациональных чисел.
Вспомним, что множество натуральны чисел обозначается латинской буквой N.
Множество целых чисел обозначается латинской буквой Z.
А множество рациональных чисел обозначается латинской буквой Q.
Во множество рациональных чисел входит множество целых и натуральных чисел в этом и заключается смысл рациональных чисел.
На рисунке можно показать множество рациональных чисел.
Но не все числа являются рациональными. Бывают еще множества различных чисел, которые в дальнейшем вы будите изучать.
Бесконечные непрериодические дроби не принадлежат множеству рациональных чисел.
Например, число е, \(\sqrt<3>\) или число \(\pi\) (читается число пи) не являются рациональными числами.
Записать число 1 в виде рационального числа?
Ответ: чтобы записать в виде рационального число 1 нужно представить его в виде дроби 1=\(\frac<1><1>\).
Докажите, что число \(\sqrt<0,0049>\) является рациональным?
Доказательство: \(\sqrt<0,0049>=0,07\)
Является ли простое число под корнем рациональным числом?
Ответ: нет. Например, любое простое число под корнем 2, 3, 5, 7, 11, 13, … не выносится из под корня и его нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому не является рациональным числом.
Рациональные числа
Тема рациональных чисел достаточно обширна. О ней можно говорить бесконечно и писать целые труды, каждый раз удивляясь новым фишкам.
Чтобы не допускать в будущем ошибок, в данном уроке мы немного углубимся в тему рациональных чисел, почерпнём из неё необходимые сведения и двинемся дальше.
Что такое рациональное число
К рациональным числам относятся следующие категории чисел:
Пример 1. Целое число 2 может быть представлено в виде дроби 
Пример 2. Смешанное число 

Значит смешанное число 
Пример 3. Десятичная дробь 0,2 может быть представлена в виде дроби 
Поскольку десятичная дробь 0,2 может быть представлена в виде дроби 
Пример 4. Бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби 
Поскольку бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби 
В дальнейшем, все числа которые можно представить в виде дроби, мы всё чаще будем называть одним словосочетанием — рациональные числа.
Рациональные числа на координатной прямой
Координатную прямую мы рассматривали, когда изучали отрицательные числа. Напомним, что это прямая линия на которой лежат множество чисел. Выглядит следующим образом:
На этом рисунке приведен небольшой фрагмент координатной прямой от −5 до 5.
Отметить на координатной прямой целые числа вида 2, 0, −3 не составляет особого труда.
Намного интереснее дела обстоят с остальными числами: с обыкновенными дробями, смешанными числами, десятичными дробями и т.д. Эти числа лежат между целыми числами и этих чисел бесконечно много.
Например, отметим на координатной прямой рациональное число 
Попробуем понять, почему дробь 
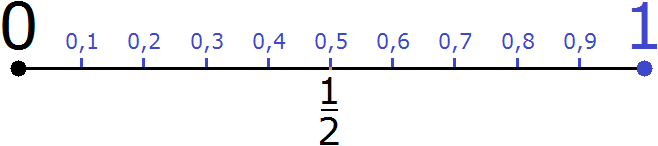
Как уже говорилось выше, между целыми числами лежат остальные числа — обыкновенные дроби, десятичные дроби, смешанные числа и т.д. К примеру, если увеличить участок координатной прямой от 0 до 1, то можно увидеть следующую картину
Видно, что между целыми числами 0 и 1 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь 

Дробь 
Десятичную дробь 0,5 можно замаскировать и под другие дроби. Из основного свойства дроби мы знаем, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то значение дроби не изменится.
Если числитель и знаменатель дроби 


А значит на координатной прямой дробь 
Пример 2. Попробуем отметить на координатной рациональное число 
Значение дроби 
Если увеличить участок координатной прямой от 1 до 2, то мы увидим следующую картину:
Видно, что между целыми числами 1 и 2 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь 
Мы увеличивали определенные отрезки на координатной прямой, чтобы увидеть остальные числа, лежащие на этом отрезке. В результате, мы обнаруживали десятичные дроби, которые имели после запятой одну цифру.
Но это были не единственные числа, лежащие на этих отрезках. Чисел, лежащих на координатной прямой бесконечно много.
Нетрудно догадаться, что между десятичными дробями, имеющими после запятой одну цифру, лежат уже другие десятичные дроби, имеющие после запятой две цифры. Другими словами, сотые части отрезка.
К примеру, попробуем увидеть числа, которые лежат между десятичными дробями 0,1 и 0,2
Ещё пример. Десятичные дроби, имеющие две цифры после запятой и лежащие между нулём и рациональным числом 0,1 выглядят так:
Пример 3. Отметим на координатной прямой рациональное число 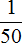
Значение дроби 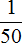
Если мы увеличим отрезок от 0 до 0,1 то увидим где точно расположилось рациональное число
Видно, что наше рациональное число 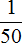
Пример 4. Отметим на координатной прямой рациональное число 0, (3)
Рациональное число 0, (3) является бесконечной периодической дробью. Его дробная часть никогда не заканчивается, она бесконечная
0,33333….и так далее до бесконечности..
И поскольку у числа 0,(3) дробная часть является бесконечной, это означает, что мы не сможем найти точное место на координатной прямой, где это число располагается. Мы можем лишь указать это место приблизительно.
Рациональное число 0,33333… будет располагаться очень близко к обычной десятичной дроби 0,3
Данный рисунок не показывает точное место расположения числа 0,(3). Это лишь иллюстрация, показывающая как близко может располагаться периодическая дробь 0,(3) к обычной десятичной дроби 0,3.
Пример 5. Отметим на координатной прямой рациональное число 



Если перевести смешанное число 

Значение дроби 
Если увеличить участок координатной прямой от 2 до 3, то мы увидим следующую картину:
Видно, что наше рациональное число 
Минус перед рациональным числом
В предыдущем уроке, который назвался умножение и деление целых чисел мы научились делить целые числа. В роли делимого и делителя могли стоять как положительные, так и отрицательные числа.
Рассмотрим простейшее выражение
В данном выражении делимое (−6) является отрицательным числом.
Теперь рассмотрим второе выражение
Здесь уже отрицательным числом является делитель (−2). Но в обоих случаях мы получаем один и тот же ответ −3.
Учитывая, что любое деление можно записать в виде дроби, мы можем рассмотренные выше примеры также записать в виде дроби:
А поскольку в обоих случаях значение дроби одинаково, минус стоящий либо в числителе либо в знаменателе можно сделать общим, поставив его перед дробью
Поэтому между выражениями 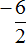
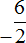
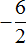
В дальнейшем работая с дробями, если минус будет нам встречаться в числителе или в знаменателе, мы будем делать этот минус общим, ставя его перед дробью.
Противоположные рациональные числа
Как и целое число, рациональное число имеет своё противоположное число.
Например, для рационального числа 


Перевод смешанных чисел в неправильные дроби
Мы знаем что для того, чтобы перевести смешанное число в неправильную дробь, нужно целую часть умножить на знаменатель дробной части и прибавить к числителю дробной части. Полученное число будет числителем новой дроби, а знаменатель остаётся прежним..
Например, переведём смешанное число 
Умножим целую часть на знаменатель дробной части и прибавим числитель дробной части:
Вычислим данное выражение:
Полученное число 5 будет числителем новой дроби, а знаменатель останется прежним:
Полностью данная процедура записывается следующим образом:
Чтобы вернуть изначальное смешанное число, достаточно выделить целую часть в дроби
Но этот способ перевода смешанного числа в неправильную дробь применим только в том случае, если смешанное число является положительным. Для отрицательного числа данный способ не сработает.
Рассмотрим дробь 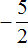
Чтобы вернуть изначальную дробь 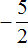
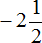
Мы получили дробь 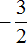
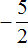
Делаем вывод, что смешанное число 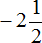
Чтобы правильно перевести отрицательное смешанное число в неправильную дробь, нужно целую часть умножить на знаменатель дробной части, и из полученного числа вычесть числитель дробной части. В этом случае у нас всё встанет на свои места
Отрицательное смешанное число 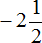


то отрицательное смешанное число 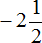

И если 
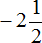

Любое смешанное число можно записать в развёрнутом виде. Положительное смешанное число 
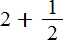
А отрицательное смешанное число 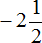
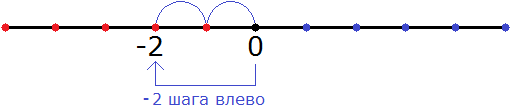
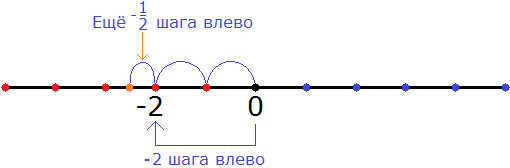
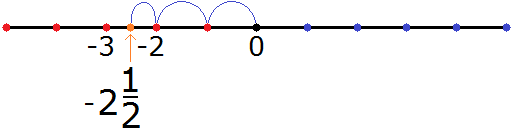
Теперь мы можем понять, почему смешанное число 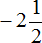
Затем, начиная от числа −2 сдвинулись ещё влево на 

В итоге, мы окажемся посередине между числами −3 и −2
Пример 2. Выделить в неправильной дроби 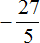
Выполним первую часть задания, а именно выделим в неправильной дроби 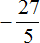
Выполним вторую часть задания, а именно переведём полученное смешанное число 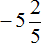
Если нет желания путаться и привыкать к новому правилу, то можно смешанное число заключить в скобки, а минус оставить за скобкой. Тогда можно будет применить старое доброе правило: умножить целую часть на знаменатель дробной части и к полученному числу прибавить числитель дробной части.
Выполним предыдущее задание этим способом, а именно переведём смешанное число 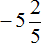
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
16 thoughts on “Рациональные числа”
Было бы лучше, чтоб после каждого шага было много задач. Так как без задач, не возможно закрепление и запоминание темы. Только ни в коем случае «один вопрос и пять вариантов ответа». Человек решая, должен быть уверен, что правильно решил задачу.
К каждому шагу дано более одного примера. Вы можете, прочитав условие, самостоятельно попытаться решить примеры.
С большим удовольствием прошёлся по материалу и освежил знания. Жаль нет продолжения. Очень всё доходчиво, спасибо.
Здравствуйте admin! С большим удовольствием повторил математику, скажите пожалуйста какие дальше темы?Очень нужно экспрессом к вышке добраться
Спасибо за сайт с удовольствием изучаю то что пропустил многие годы назад. Но хотелось бы узнать профессию автора и квалификацию и о том дойдет ли админ до разделов высшей математики.
По вашим статьям надо учебники писать. Если бы в у нас в книгах все так понятно писали все бы были отличниками.
Здравствуйте мы продолжаем учится товарищ ленин сказал учиться не поздно а ещё желаю увидеть вышие матиматику в адресе

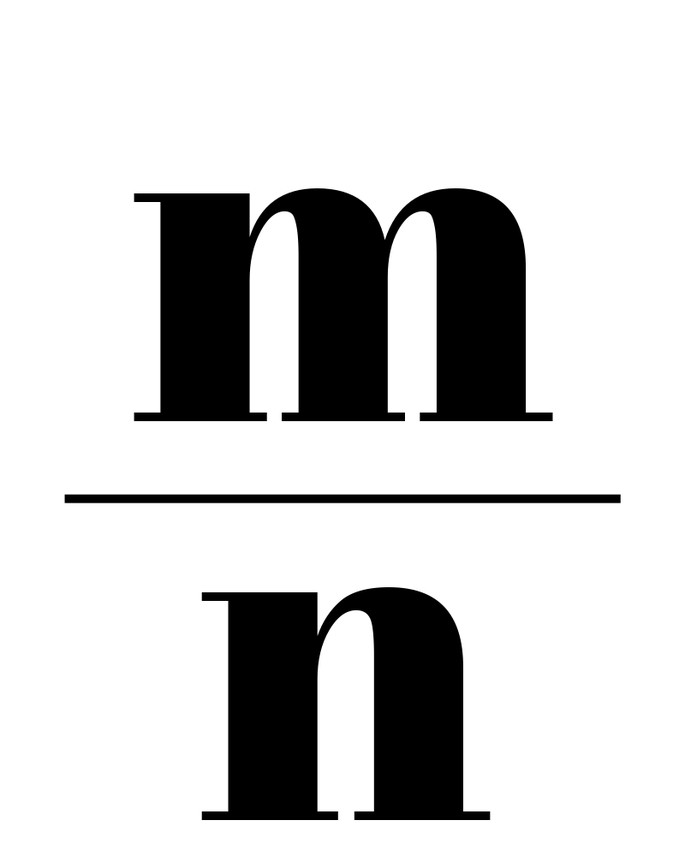

 ;
; ;
; .
.