Момент инерции что это сопромат
изучаем сопротивление материалов
Момент инерции плоских сечений
Осевым моментом инерции сечения (second moment of area или second moment of inertia) относительно оси x называется сумма произведений элементарных площадок dA на квадрат их расстояний до данной оси, численно равная интегралу
$$J_x = \int_y^2dA$$
Полярным моментом инерции сечения относительно данной точки
(называемого полюсом ) называется сумма произведений элементарных площадок dA на квадрат их расстояний до этой точки:
$$J_ <\rho>= \int_<\rho>^2dA$$
где [math]\rho[/math] – расстояние от площадки dA до полюса, относительно которой вычисляется полярный момент инерции.
Центробежным моментом инерции сечения относительно осей x и y называется сумма произведений элементарных площадок dA на их расстояния до этих осей:
$$J_
где x,у — расстояние от элементарной площадки dA до осей х и y (смотри рисунок).
Центробежный момент инерции может быть положительным, отрицательным и, в частном случае, равным нулю. Если взаимно перпендикулярные оси x и y или одна из них являются осями симметрии фигуры, то относительно таких осей центробежный момент инерции равен нулю. [math]J_
Зависимость между моментами инерции относительно параллельных осей
Момент инерции относительно любой оси равен моменту инерции
относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.
Момент инерции относительно центральной оси называется центральным моментом инерции сечения.
Из формул следует, что момент инерции относительно центральной оси меньше, чем момент инерции относительно любой нецентральной оси сечения, параллельной центральной.
Зависимость между моментами инерции при повороте осей
$$J_
$$J_
Лекция 5. Моменты инерции поперечного сечения
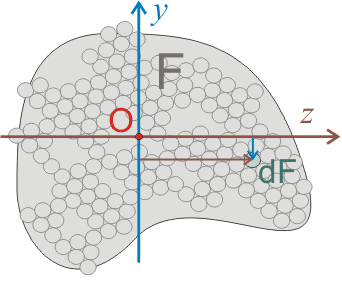
Иногда при расчете строительных конструкций необходимо знать значение момента инерции поперечного сечения. При этом само понятие момент инерции знает любой инженер, а вот откуда взялось это понятие, и какой его физический смысл, могут объяснить не многие. Как правило в любом справочнике или учебнике по сопротивлению материалов дается приблизительно следующее определение для момента инерции:
I = ∑ri 2 dF i =∫r 2 dF (1.1)
В принципе и определение и формула, его описывающая, не сложные и запомнить их намного легче, чем вникнуть в суть. Но все-таки попробуем разобраться, что же такое момент инерции и откуда он взялся.
Понятие момент инерции пришло в сопромат и строительную механику из другого раздела физики, изучающего кинематику движения, в частности вращательное движение. Но все равно начнем издалека.
Я точно не знаю, упало ли Исааку Ньютону на голову яблоко, упало оно рядом, или вообще не падало, теория вероятности допускает все эти варианты (к тому же в этом яблоке слишком много от библейской легенды о древе познания), однако я уверен, что Ньютон был наблюдательным человеком, способным делать выводы из своих наблюдений. Так наблюдательность и воображение позволили Ньютону сформулировать основной закон динамики (второй закон Ньютона), согласно которому масса тела m, умноженная на ускорение a, равна действующей силе Q (вообще-то более привычным для силы является обозначение F, но так как дальше мы будем иметь дело с площадью, которая также часто обозначается как F, то я использую для внешней силы, рассматриваемой в теоретической механике как сосредоточенная нагрузка, обозначение Q, сути дела это не меняет):
Q = ma (1.2)
По мне величие Ньютона именно в простоте и понятности данного определения. А еще, если учесть, что при равноускоренном движении ускорение а равно отношению приращения скорости ΔV к периоду времени Δt, за который скорость изменилась:
при Vо = 0 a = v/t (1.3.2)
то можно определить основные параметры движения, такие как расстояние, скорость, время и даже импульс р, характеризующий количество движения:
p = mv (1.4)
Например, яблоко, падающее с разной высоты под действием только силы тяжести, будет падать до земли разное время, иметь разную скорость в момент приземления и соответственно разный импульс. Другими словами, яблоко, падающее с бóльшей высоты, будет дольше лететь и сильнее треснет по лбу незадачливого наблюдателя. И все это Ньютон свел к простой и понятной формуле.
А еще Ньютон сформулировал закон инерции (первый закон Ньютона): если ускорение а = 0, то в инерциальной системе отсчета невозможно определить, находится ли наблюдаемое тело, на которое не действуют внешние силы, в состоянии покоя или движется прямолинейно с постоянной скоростью. Это свойство материальных тел сохранять свою скорость, пусть даже и нулевую, называется инертностью. Мерой инертности является инерционная масса тела. Иногда инерционная масса называется инертной, но сути дела это не меняет. Считается, что инерционная масса равна гравитационной массе и потому часто не уточняется, какая именно масса имеется в виду, а упоминается просто масса тела.
Не менее важным и значимым является и третий закон Ньютона, согласно которому сила действия равна силе противодействия, если силы направлены по одной прямой, но при этом в противоположные стороны. Не смотря, на кажущуюся простоту, и этот вывод Ньютона гениален и значение этого закона трудно переоценить. Об одном из применений этого закона чуть ниже.
Однако данные положения справедливы только для тел, движущихся поступательно, т.е. по прямолинейной траектории и при этом все материальные точки таких тел двигаются с одинаковой скоростью или одинаковым ускорением. При криволинейном движении и в частности при вращательном движении, например, когда тело вращается вокруг своей оси симметрии, материальные точки такого тела перемещаются в пространстве с одинаковой угловой скоростью w, но при этом линейная скорость v у различных точек будет разная и эта линейная скорость прямо пропорциональна расстоянию r от оси вращения до этой точки:
v = wr (1.5)
при этом угловая скорость равна отношению приращения угла поворота Δφ к периоду времени Δt, за который угол поворота изменился:
при φо = 0 w = φ/t (1.7.2)
соответственно нормальное ускорение аn при вращательном движении равно:
an = v 2 /r = w 2 r (1.8)
И получается, что для вращательного движения мы не можем прямо использовать формулу (1.2), так как при вращательном движении одного только значения массы тела недостаточно, требуется еще знать распределение этой массы в теле. Получается, что чем ближе материальные точки тела к оси вращения, тем меньшую силу требуется приложить, чтобы заставить тело вращаться и наоборот, чем дальше материальные точки тела от оси вращения, тем большую силу нужно приложить, чтобы заставить тело вращаться (в данном случае речь идет о приложении силы в одной и той же точке). К тому же при вращении тела более удобно рассматривать не действующую силу, а вращающий момент, так как при вращательном движении точка приложения силы также имеет большое значение.
Поразительные свойства момента нам известны со времен Архимеда и если применить понятие момента к вращательному движению, то значение момента М будет тем больше, чем больше расстояние r от оси вращения до точки приложения силы F (в строительной механике внешняя сила часто обозначается как Р или Q):
М = Qr (1.9)
Из этой также не очень сложной формулы выходит, что если сила будет приложена по оси вращения, то никакого вращения не будет, так как r = 0, а если сила будет приложена на максимальном удалении от оси вращения, то и значение момента будет максимальным. А если мы подставим в формулу (1.9) значение силы из формулы (1.2) и значение нормального ускорения и формулы (1.8), то получим следующее уравнение:
М = mw 2 r·r = mw 2 r 2 (1.10)
В частном случае когда тело является материальной точкой, имеющей размеры намного меньше, чем расстояние от этой точки до оси вращения, уравнение (1.10) применимо в чистом виде. Однако для тела, вращающегося вокруг одной из своих осей симметрии, расстояние от каждой материальной точки составляющей данное тело, всегда меньше одного из геометрических размеров тела и потому распределение массы тела имеет большое значение, в этом случае требуется учесть эти расстояния отдельно для каждой точки:
M = ∑r i 2 w 2 mi (1.11.1)
И тогда получается, что согласно третьему закону Ньютона в ответ на действие вращающего момента будет возникать так называемый момент инерции I. При этом значения вращающего момента и момента инерции будут равны, а сами моменты направлены в противоположные стороны. При постоянной угловой скорости вращения, например w = 1, основными величинами, характеризующими вращающий момент или момент инерции будут масса материальных точек, составляющих тело, и расстояния от этих точек до оси вращения. В итоге формула момента инерции примет следующий вид:
Ic = ∫ρr 2 dV (1.13)
Таким образом момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении.
Все круг замкнулся. И тут может возникнуть вопрос, какое отношение все эти законы динамики и кинематики имеют к расчету статических строительных конструкций? Оказывается, что ни на есть самое прямое и непосредственное. Во-первых потому, что все эти формулы выводились физиками и математиками в те далекие времена, когда таких дисциплин, как «Теоретическая механика» или «Теория сопротивления материалов» попросту не существовало. А во-вторых потому, что весь расчет строительных конструкций и построен на основе указанных законов и формулировок и пока ни кем не опровергнутом утвержении о равенстве гравитационной и инертой масс. Вот только в теории сопротивления материалов все еще проще, как ни парадоксально это звучит.
Iр = ∫r 2 dF (2.1) → (1.1)
Так как в теории сопротивления материалов часто рассматриваются прямоугольные сечения, да и прямоугольная система координат более удобна, то при решении задач обычно рассматриваются два осевых момента инерции поперечного сечения:
Iz = ∫y 2 dF (2.2.1)
Iy = ∫z 2 dF (2.2.2)
Рисунок 1. Значения координат при определении осевых моментов инерции.
В то же время теория сопротивления материалов рассматривает именно поперечное сечение, для которого важны ширина и высота, а длина не учитывается. Само собой при решении задач теории сопротивления материалов, также порой достаточно сложных используются все те же привычные оси х и у. Мне такое положение дел кажется не совсем правильным, так как не смотря на разницу, это все же смежные задачи и потому будет более целесообразным использование единых осей для рассчитываемой конструкции.
Значение полярного момента инерции в прямоугольной системе координат будет:
Iр = ∫r 2 dF = ∫y 2 dF + ∫z 2 dF (2.3)
Ixz = ∫xzdF (2.4)
Среди осей прямоугольной системы координат, проходящих через центр тяжести поперечного сечения, есть две взаимно-перпендикулярные оси, относительно которых осевые моменты инерции принимают максимальное и минимальное значение, при этом центробежный момент инерции сечения Izy = 0. Такие оси называют главными центральными осями поперечного сечения, а моменты инерции относительно таких осей – главными центральными моментами инерции
Когда в теории сопротивления материалов речь заходит о моментах инерции, то как правило в виду имеются именно главные центральные моменты инерции поперечного сечения. Для квадратных, прямоугольных, круглых сечений главные оси будут совпадать с осями симметрии. Моменты инерции поперечного сечения также называют геометрическими моментами инерции или моментами инерции площади, но суть от этого не изменяется.
I = Ic + r 2 F (2.5)
и тогда полярный статический момент поперечного сечения будет:
Sр = ∫rdF (2.7)
Как видим, определение статического момента сходно с определением момента инерции. Но есть и принципиальная разница. Статический момент потому и называется статическим, что для тела, на которое действует сила тяжести, статический момент равен нулю относительно центра тяжести. Другими словами такое тело находится в состоянии равновесия, если опора приложена к центру тяжести тела. А согласно первому закону Ньютона такое тело или находится в состоянии покоя или движется с постоянной скоростью, т.е. ускорение = 0. А еще с чисто математической точки зрения статический момент может быть равен нулю по той простой причине, что при определении статического момента необходимо учитывать направление действия момента.
Sz = ∫ydF = 0 (2.8)
А еще этот великий ноль позволяет определять опорные реакции строительных конструкций. Если рассматривать строительную конструкцию, к которой приложена например сосредоточенная нагрузка Q в некоторой точке, то такую строительную конструкцию можно рассматривать, как тело с центром тяжести в точке приложения силы, а опорные реакции в этом случае рассматриваются, как силы приложенные в точках опор. Таким образом зная значение сосредоточенной нагрузки Q и расстояния от точки приложения нагрузки до опор строительной конструкции, можно определить опорные реакции.
Например для шарнирно опертой балки на двух опорах значение опорных реакций будет пропорционально расстоянию до точки приложения силы, а сумма реакций опор будет равна приложенной нагрузке. Но как правило при определении опорных реакций поступают еще проще: за центр тяжести принимается одна из опор и тогда сумма моментов от приложенной нагрузки и от остальных опорных реакций все равно равна нулю. В этом случае момент от опорной реакции относительно которой составляется уравнение моментов, равен нулю, так как плечо действия силы = 0, а значит в сумме моментов остаются только две силы: приложенная нагрузка и неизвестная опорная реакция (для статически определимых конструкций).
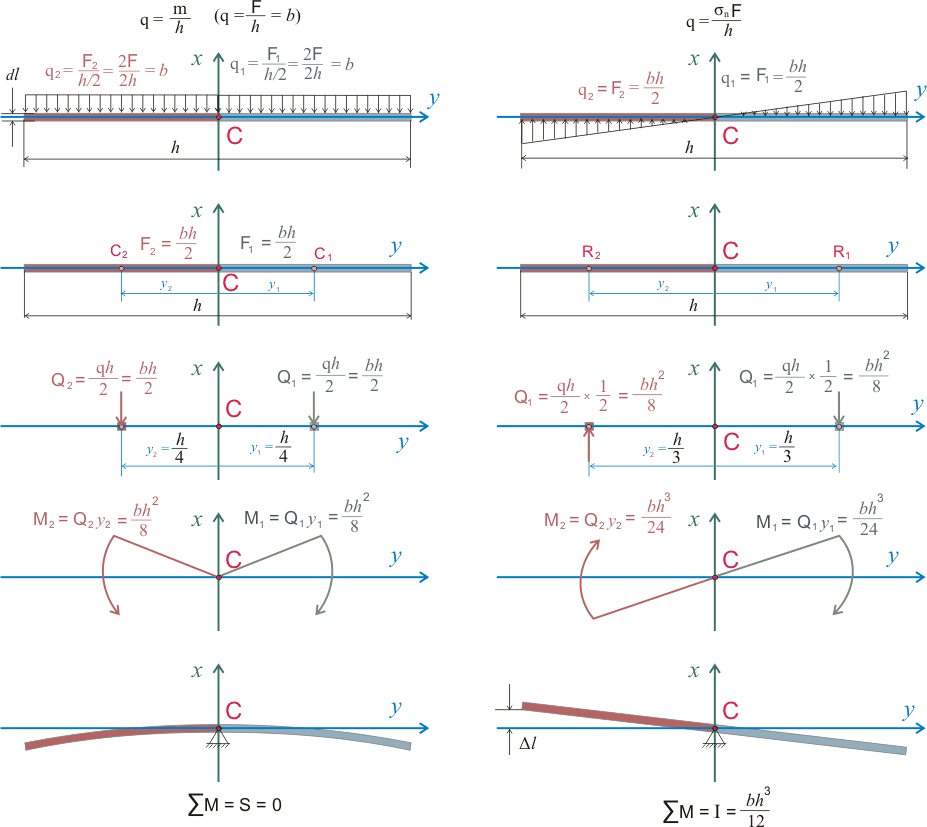
Таким образом принципиальная разница между статическим моментом и моментом инерции в том, что статический момент характеризует сечение, которое сила тяжести как бы пытается сломать пополам относительно центра тяжести или оси симметрии, а момент инерции характеризует тело, все материальные точки которого перемещаются (или пытаются переместиться в одном направлении). Возможно, более наглядно представить себе эту разницу помогут следующие достаточно условные расчетные схемы для прямоугольного сечения:
Рисунок 2. Наглядная разница между статическим моментом и моментом инерции.
А теперь вернемся еще раз к кинематике движения. Если проводить аналогии между напряжениями, возникающими в поперечных сечениях строительных конструкций, и различными видами движения, то в центрально растягиваемых и центрально сжатых элементах возникают напряжения равномерные по всей площади сечения. Эти напряжения можно сравнить с действием некоторой силы на тело, при котором тело будет двигаться прямолинейно и поступательно. А самое интересное, это то, что поперечные сечения центрально-растянутых или центрально сжатых элементов действительно движутся, так как действующие напряжения вызывают деформации. И величину таких деформаций можно определить для любого поперечного сечения конструкции. Для этого достаточно знать значение действующих напряжений, длину элемента, площадь сечения и модуль упругости материала, из которого изготовлена конструкция.
А еще момент инерции позволяет определить момент сопротивления сечения. Для этого момент инерции нужно просто разделить на расстояние от центра тяжести сечения до наиболее удаленной точки сечения, для прямоугольного сечения на h/2. А так как исследуемые сечения не всегда симметричны, то значение момента сопротивления может быть разным для разных частей сечения.
А началось все с банального яблока. хотя нет, начиналось все со слова.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Классная статья, всё понятно, с рисунками, красота!
В данной статье сказано: Получается, что чем ближе материальные точки тела к оси вращения, тем меньшую силу требуется приложить, чтобы заставить тело вращаться и наоборот, чем дальше материальные точки тела от оси вращения, тем большую силу нужно приложить, чтобы заставить тело вращаться.
Не наоборот ли? Ведь расстояние от оси является плечом. Чем больше плечо, тем меньше силы нужно приложить для того, чтобы заставит тело вращаться. Или я вновь неправильно всё понял. Упс:(
Возможно я недостаточно ясно выразился, поэтому внес в статью соответствующую поправку. В данном случае речь идет о силе, приложенной в одной и той же точке. Например в первом случае, когда материальная точка расположена близко к центру вращения, то необходимая для вращения сила, приложенная на таком же расстоянии, будет одной. Во втором случае плечо приложения силы не изменится, а вот материальная точка будет от центра вращения значительно дальше, поэтому и сила для ее вращения потребуется больше, хотя при этом масса материальных точек в обоих случаях остается одинаковой.
Надеюсь, теперь понятно объяснил.
То самое объяснение которое так долго я искал. Лучшее на мой взгляд. Спасибо, стало все гораздо яснее!
Рад был помочь, пусть и виртуально.
Здравствуйте!
Вы пишите «соответственно нормальное ускорение аn при вращательном движении равно». На основании чего это соответственно? Для наблюдателя никакого соответствия не видно. Просто в воздухе возникла формула.
Дмитрий, искренне рад, что статья вам понравилась.
Уважаемый Доктор, а Вы не думали выпустить свои труды в печатном виде?
Не думаю, что это будет иметь успех. К тому же труд еще не завершен, многие аспекты теории сопротивления материалов еще не нашли отражения в моих статьях (и теперь вряд ли найдут, так как сил и желания на продолжение работы у меня уже нет).
Да я вроде целую статью посвятил объяснению осевых моментов инерции и добавить мне тут особенно нечего. Пожалуйста, перечитайте данную статью более внимательно и физический смысл вам откроется. Если нет, то обращайтесь.
Подскажите, где я ошибаюсь?
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Момент инерции сечения
Меня часто спрашивают: «…а что такое моменты инерции в сопротивлении материалов и зачем они вообще?» Об этом в сегодняшней теме
Моменты инерции сечения из простых фигур
Начнем с моментов инерции простых фигур и на их примере выясним для сложных и составных сечений.
Начать объяснение о том, что такое моменты инерции нужно с того, что спросить, а что такое площадь?
Обычная площадь квартиры, огорода сечения стержня? Зачем она и почему?
Так вот площадь это характеристика которую придумали и вывели для разных фигур, чтобы была возможность сравнивать земельные наделы. Не всегда они были прямоугольные или квадратные. А сравнить кто сколько получил в надел было нужно. Вот и вывели такую закономерность для прямоугольника, что если перемножить стороны — получим величину, которую можно будет сравнить с перемноженной высотой на основание деленное пополам для треугольника или для круга Пи умножить на эр в квадрате )). Т.е. площади простых фигур
Что касается моментов инерции в сопротивлении материалов, то тут они появились, когда стало понятно, что есть какая то геометрически измеримая величина для разных форм сечения, которая позволит сравнить сопротивляемость этих сечений изгибу.
Проще говоря бревно, которое выполняет роль балки и изгибается может иметь форму прямоугольника, квадрата или круга, а нам нужно сравнить их сопротивляемость изгибу. Вот для этих целей выводили формулу напряжений и оказалось, что в числителе оказался изгибающий момент, а в знаменателе момент инерции:
на балке изображены главные центральные оси z y
прогибы для таких балок будут разными относительно осей z и y, т.к. моменты инерции будут разные.
Вывод моментов инерции для простых фигур
Так вот ниже я приведу видео уроки, плейлист, в котором один за одним выведены моменты инерции для простых фигур, а именно для прямоугольника, треугольника и круга. А затем приводится стандартный расчет моментов инерции для более сложной фигуры, которая состоит из нескольких простых. Всегда сложную фигуру можно разбить на несколько простых. Исходя из этого расчет и ведется.
Моменты инерции измеряются в единицах длины в 4 степени, т.е. см⁴ или м⁴. Чаще всего используется см⁴, т.к. такие единицы измерения приведены в сортаменте прокатной стали.
Момент инерции, это величина, которая показывает сопротивляемость сечения изгибу. На примере линейки хорошо понятно что изгиб в одной плоскости и изгиб в другой плоскости будут сильно отличаться, хотя площадь сечения не меняется. Вот это и было выведено в формуле для напряжений и для прогибов. Что величина, которая сопротивляется изгибающему моменту есть интеграл до координаты центра тяжести площадки в квадрате на площадь элементарной площадки.
Центральными осями называют оси, которые проходят через центр тяжести сечения
Главные оси располагаются в сечении таким образом, что центробежный момент относительно них равен нулю. Т.е. это максимальный и минимальный осевые моменты инерции
Оси, которые проходят через центр тяжести сечения и центробежный момент инерции относительно них равен нулю. При этом данные осевые моменты инерции являются экстремальными, т.е. имеют максимальное и минимальное значение. Именно относительно этих осей ведут расчет и к ним приводят нагрузки. Т.е. если какое нибудь внешнее усилие проходит в стороне от главных центральных осей. Это усилие переносят соблюдая правила переноса к главным центральным осям. Только после этого рассматривают действие сил и находят внутренние усилия относительно главных центральных осей инерции.
При вычислении моментов инерции осевых, при переходе от одних осей к другим появляется центробежный момент инерции, как составляющая пары осевых моментов инерции. И только для главных осей центробежные моменты инерции равны нулю. Именно эти оси мы и отыскиваем в наших расчетах. Поэтому мы ищем величину центробежного момента инерции для не главных осей и из свойства, что главные центральные оси это такие оси, относительно которых центробежный момент инерции равен нулю, находим положение главных центральных осей.
Моменты инерции для прямоугольника
#Сопромат, Моменты инерции. Прямоугольник. Вывод моментов инерции для прямоугольника.
Сопротивление материалов и Моменты инерции для прямоугольника. Понятие моментов инерции, формулы и вывод для прямоугольника. Осевые центробежный моменты инерции. для треугольника вывод моментов инерции в этом видео: https://www.youtube.com/embed/_pixohVoc-4?vq=hd720 Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2018-04-09
моменты инерции для прямоугольника для главных центральных осей равны, формула
моменты инерции для прямоугольника для осей проходящих через основные размеры равны, формула
Моменты инерции для треугольника
Сопротивление материалов, Моменты инерции для треугольника. Сопромат вывод моментов инерции
Сопротивление материалов и Моменты инерции для треугольника. Сопромат вывод моментов инерции для простых фигур. Моменты инерции для треугольника. Моменты инерции для осей в треугольнике, которые проходят через основные размеры. Вывод и пояснение к этой теме сопротивления материалов. для прямоугольника вывод моментов инерции в этом видео: https://www.youtube.com/watch?v=v1TE1UW_sRE&feature=youtu.be Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2018-04-09
Моменты инерции треугольника относительно произвольых осей
Момент инерции круга. Моменты инерции простых фигур. #сопромат
Вывод моментов инерции для круга. Видео урок из темы «Моменты инерции простых фигур». В видео приведен вывод момента инерции полярного, в полярной системе координат Ip Затем выведены моменты инерции осевые Iz, Iy. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2019-09-14
Моменты инерции. Оси центральные и главные. Что это и где. #сопромат
Центральные оси — любая пара взаимно перпендикулярных осей, которые проходят через центр тяжести фигуры Главные оси — оси для которых центробежный момент инерции равен нулю, а осевые моменты имеют максимум и минимум. Об этом и многом другом в видео уроке по моментам инерции в сопротивлении материалов Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2019-09-14