Найди ложные высказывания и построй их отрицания докажи что построенные отрицания истины
Помогите найти ложные высказывания. № 27 ГДЗ Математика 6 класс Дорофеев, Петерсон Часть 1.
Найди ложные высказывания, построй их отрицания и докажи, что отри-
цания истинны.
1) Все решения неравенства 1
1) Не все решения неравенства 2 ≤ х
Здравствуйте! Помогите установить соответствие между неравенствами и их решениями: ( Подробнее. )
Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из ( Подробнее. )
Вырежи из бумаги 20 одинаковых произвольных треугольников и составь
из них паркет. Всегда ли это можно сделать? Почему?
Строить отрицания элементарных высказываний.
Типовые задания с решениями
Пример 1.Среди нижеследующих предложений выделить высказывания. Определить их значение истинности.
а) Спешите делать добро!
б) Закон всемирного тяготения открыл И.Ньютон.
в) В солнечную погоду полезны солнечные очки.
г) Когда вы будете в Париже?
д) Число 9 является простым.
е) Сегодня был вкусный обед.
ж) Некоторые люди имеют голубые глаза.
з) Все животные хищники.
Решение. Из всех предложений высказываниями являются только б), в), д), ж) и з). Высказывания б), в) и ж) являются истинными, а высказывание д) и з) – ложным.
Высказывания ж) и з) являются высказываниями с кванторами. Восклицательное предложение а) и вопросительное предложение г) не являются высказываниями. Предложение е) не является высказыванием из-за субъективности понятия «вкусный обед».
Пример 2.Выделить высказывательные формы (предикаты) среди следующих предложений:
Решение. Отрицанием высказывания «число 132 делится на 9» является высказывание «число 132 не делится на 9». Отрицанием высказывания «5>4» является высказывание «5 не больще 4», или «5£4».
Пример 5.Построить отрицания высказываний, содержащих квантор:
а) все натуральные числа делятся на 3;
б) некоторые нечетные числа делятся на 4.
а) Первый вариант: неверно, что все натуральные числа делятся на 3.
Второй вариант: существуют натуральные числа, которые не делятся на 3.
б) Первый вариант: неверно, что некоторые нечетные числа делятся на 4.
Второй вариант: Каждое нечетное число не делится на 4.
Задания для самостоятельной работы (базовый уровень)
1.Какие из следующих предложений являются высказываниями? Какие из высказываний истинны, а какие ложны?
ж) Некоторые люди мечтают иметь автомобиль. з) При замерзании вода расширяется. и) Любые три отрезка могут быть сторонами треугольника.
к) При делении нуля на любое число получается нуль.
2. Выясните, какие предложения являются высказываниями, а какие предикатами, если:
а) 3×5+5>27; б) 9×3+8=35; в) х-5=4; г) 3 

ж) хотя бы одно из чисел 1,2,3 является решением уравнения х 
4.Какие из следующих высказываний содержат квантор общности, а какие – квантор существования?
а) Все кустарники являются растениями?
б) Существуют числа, кратные 17?
в) Каждое натуральное число является целым.
г) На всякого мудреца довольно простоты.
д) Найдется такой день недели, который будет выходным.
е) Некоторые пассажиры предпочитают ехать без билета.
а) Сумма цифр числа 312 равна 6.
б) Число 27 кратно 8.
в) число 2 является корнем уравнения х+1=4.
г) 9 – однозначное число.
6. Образуйте отрицания следующих высказываний двумя способами и определите, что истинно, само высказывание или его отрицание:
а) В любом треугольнике сумма внутренних углов равна 180 
в) В некоторых прямоугольниках диагонали не равны.
г) По крайней мере, одно из чисел 10, 11, 12 делится на 2.
д) Все насекомые – вредители.
е) Существуют равносторонние треугольники.
ж) Всякие два угла не равны.
з) Некоторые параллельные прямые не пересекаются.
и) Найдется треугольник с двумя прямыми углами.
к) Во всяком треугольнике сумма двух любых сторон больше третьей.
7. Постройте отрицания следующих высказываний, встречающихся в начальной школе:
а) Для любых чисел а и b верно равенство: а+ b = b +а.
б) Для любых чисел а, b и с верно равенство: а+ (b+с) =(а+ b)+с.
в) При умножении любого числа на единицу получается это же число.
Задания для самостоятельной работы (повышенный уровень)
2. Какие из следующих предложений являются истинными (ложными) высказываниями, а какие высказываниями не являются. Выделите логическую структуру высказываний.
а) Всякое натуральное число n при делении на 3 дает остаток 0,1 или 2.
б) Существует число х, не являющееся квадратом рационального числа.
в) «Пролетарии всех стран, соединяйтесь!»
г) «Всякий кулик свое болото хвалит».
д) Некоторые сотрудники фирмы получат отпуск зимой.
е) Не каждое однозначное число является простым или составным.
ж) Не всякий треугольник имеет два острых угла.
з) Существуют геометрические фигуры, не имеющие площади.
и) Из леса каждый возвращается с корзиной грибов или ягод.
А: «Сегодня температура воздуха в Москве ниже » и «Сегодня температура воздуха в Москве выше 5 
а) Могут ли эти высказывания быть одновременно истинными?
б) Являются ли они отрицаниями друг друга?
4. Найдите значения истинности высказываний А и В и объясните, почему они не являются отрицаниями друг друга:
б) А – «Все треугольники являются равнобедренными», В – «Все треугольники не являются равнобедренными»;
в) А – «Некоторые слова могут быть разделены на слоги», В – «Некоторые слова не могут быть разделены на слоги»
5. Выясните, какие из высказываний каждой пары являются отрицаниями друг друга:
а) В книге более 100 страниц. В книге не более 100 страниц.
б) Эта гвоздика красная. Эта гвоздика розовая.
в) Эта гвоздика красная. Эта гвоздика не красная.
г) Данное слово – существительное. Данное слово – прилагательное.
6. Даны высказывания:
А:»В Черном море вода соленая»,
В: «Мурзилка – детский журнал»,
С: «К.И.Чуковский – зарубежный писатель»,

а) Образуйте отрицания данных высказываний.
б) Сформулируйте отрицания высказываний 

в) Сравните значения истинности высказываний А и 

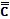
Какой вывод можно сделать?
7. Сформулируйте данные высказывания иначе, используя закон двойного отрицания:
а) Неверно, что сегодня не учебный день.
б) Неверно, что 6 – нечетное число.
в) Неверно, что Санкт-Петербург не находится на берегу Невы.
г) Неверно, что заяц не зверь.
8.Докажите, что следующие пары высказываний не являются отрицаниями друг друга:
а) Все деревья являются хвойными.
Все деревья не являются хвойными.
б) Существуют числа, кратные 7.
Существуют числа, не кратные 7.
в) Все птицы имеют черную окраску.
Все птицы не имеют черной окраски.
9.Дано высказывание А: «Все учащиеся группы сдали экзамен по математике». Укажите среди высказываний отрицание высказывания А:
а) Некоторые учащиеся группы не сдали экзамен по математике по математике.
б) Все учащиеся группы не сдали экзамен по математике.
в) Не всеучащиеся группы сдали экзамен по математике.
г) Ни один учащийся группы не сдал экзамен по математике.
10.Среди следующих предложений укажите те, которые являются отрицаниями высказывания В –«Некоторые учащиеся класса – отличники».
а) Ни один из учащихся класса не является отличником.
б) Некоторые учащиеся класса не являются отличниками.
в) Не все учащиеся класса – отличники.
г) Все учащиеся класса не являются отличниками.
11.Опровергните следующие утверждения, показав, что их отрицания истинны:
а) Все животные – млекопитающие.
б) Любое действительное число является натуральным.