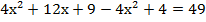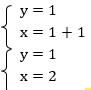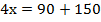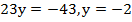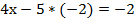Как доказать что число кратно 125
Что такое кратное число
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.
Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.
Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.
Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.
Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).
А у чисел, которые участвуют в делении, есть определенные названия:
Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.
Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.
Одно число называется кратным другому, если его можно на него поделить без остатка.
Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.
Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.
12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6
Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.
Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:
Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.
Таблицы чисел кратных 2,3,4,5,6,7,9
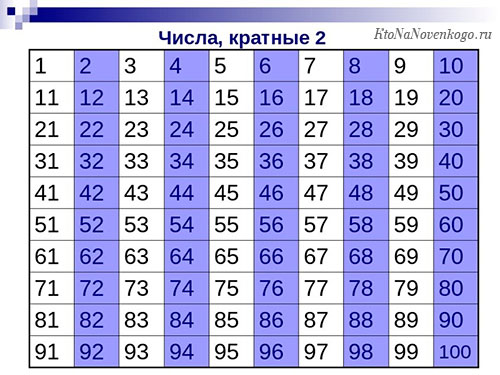
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.
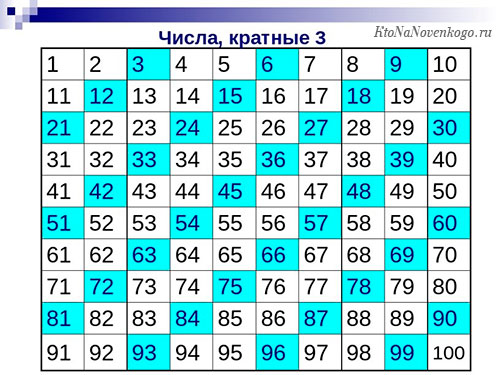
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.
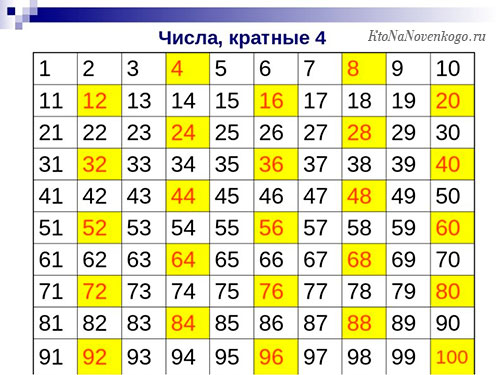
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.
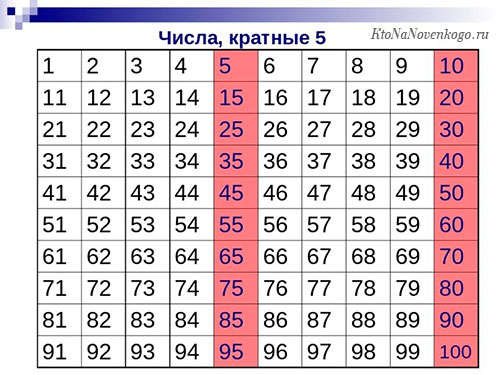
А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.
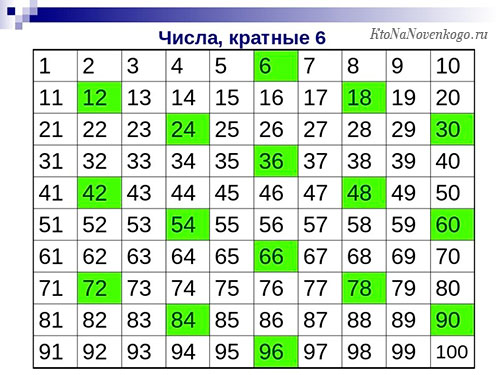
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.
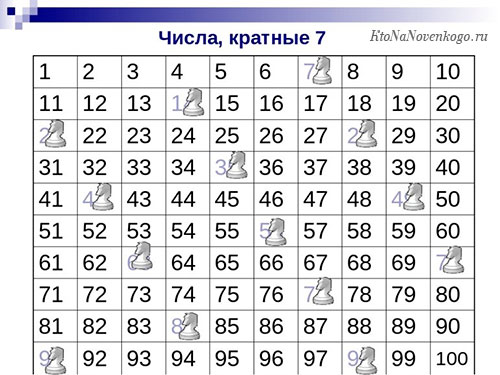
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».
И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.
Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.
| Числа, кратные 9 | 27 | 198 | 5 877 | 3 816 | 117 | 72 |
|---|---|---|---|---|---|---|
| Сумма | 9 | 18 | 27 | 18 | 9 | 9 |
Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.
Вместо заключения
А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.
Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Тут надо запомнить всего лишь одно, то что число должно делиться без остатка, а дальше все будет просто и для этого даже никакой таблицы не надо.
Но кстати за таблицы все равно спасибо. Сейчас моя как раз в школе проходит, и распечатал ей, чтобы было просто понятнее. Не знаю, нас как то лучше обучали что ли. У меня эта тема вообще в школе трудностей никаких не вызвала, а современные школьники вообще не понимают что это такое.
Доказательство кратности и уравнение
Существует обратная задача – разложить многочлен на множители, она решается также с помощью формул сокращенного умножения.
Пример 6: доказать что число 
Очевидно, что если мы будем выполнять все вычисления, это будет сложно и долго, но если заметить формулу, то работа значительно упрощается. Итак, мы видим разность кубов. Распишем выражение:
В результате преобразований мы получили выражение, один из множителей которого равен 25, очевидно, что это выражение кратно 25.
Пример 7: решить уравнение:
Напомним, что решить уравнение – означает найти такие значения х, которые обращают выражение в верное числовое равенство. Распишем в уравнении квадрат суммы и разность квадратов:
Соберем неизвестные слева, а свободные члены справа и приведем подобные:
Из полученного элементарного уравнения найдем значение х:
Запишем еще несколько формул, которые можно вывести:
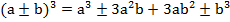
Чтобы вывести данные формулы, нужно выполнить умножение скобок, и вы убедитесь в их справедливости.
Итоги урока
Вывод: мы рассмотрели формулы сокращенного умножения, записали вид основных из них и некоторые доказали. Мы рассмотрели примеры различной сложности, чтобы окончательно закрепить данный материал.
1. Преобразовать выражение в многочлен:
а) (а – 2)(а + 2); б) (7а + 8в)²; в) (с³ – 0,1)².
2. Решить уравнение:
3. Упростить выражение и найдите его значение:
Урок 5:Повторение. Разложение многочленов на множители.
На данном уроке мы вспомним все изученные методы разложения многочлена на множители, рассмотрим примеры к ним.
1. Методы разложения многочленов на множители.
Напомним, что многочлен есть алгебраическая сумма одночленов, а одночлен – это произведение чисел и степеней.
Вспомним способы разложения многочлена на множители.
1. В каждом члене многочлена может быть общий множитель, отсюда первый способ – метод вынесения общего множителя за скобки, то есть такого множителя, который присутствует во всех членах многочлена. Рассмотрим пример 1, вынесем общий множитель за скобки, для этого определим, какие переменные представлены во всех членах, и вынесем их в минимальной степени:

Напомним, что, перемножив вынесенный множитель на скобку, можно проверить правильность вынесения.
В обоих членах есть скобка 
2. Метод группировки. Не всегда в многочлене можно вынести общий множитель. В таком случае нужно его члены разбить на группы таким образом, чтобы в каждой группе можно было вынести общий множитель, и постараться разбить так, чтобы после вынесения множителей в группах появился общий множитель у всего выражения, и можно было бы продолжить разложение. Рассмотрим пример 3:

Сгруппируем первый член со вторым, третий с четвертым и вынесем общие множители в группах:
У выражения появился общий множитель. Вынесем его:

3. Применение формул сокращенного умножения. Рассмотрим пример 4:
Мы расписали заданный многочлен по известной формуле разности кубов.
Комментарий: мы увидели в заданном многочлене формулу суммы кубов и разложили его.
4. Метод выделения полного квадрата. Он базируется на формулах квадрата суммы и квадрата разности. Напомним их:

Особенность этих формул в том, что в них есть квадраты двух выражений и их удвоенное произведение. Рассмотрим пример 6:

Итак, первое выражение – это 
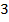
Свернем полный квадрат разности:

Преобразуем полученное выражение, применяя формулу разности квадратов, напомним, что разность квадратов двух выражений есть произведение суммы на их разность:

Напомним, что, перемножив скобки, можно проверить правильность разложения.
Подведение итогов урока
Вывод: мы вспомнили все изученные методы разложения многочленов на множители и рассмотрели примеры. Вспомнили определение и некоторые свойства алгебраических дробей, решили несколько типовых задач, с ними связанных.
1. Вынести общий множитель за скобки:
а) 8х – 8у; б) 5ху – 7х; в) 25х³ – 10х² + 5х;
2. Решить уравнение:
а) (7х – 10)(х + 5) = 0; б) 12у² – 60у = 0; в) х³ + х² – 4х – 4 = 0.
3. Докажите, что выражение:
а) 5¹³ – 5¹¹ делится на 24; б) 125³ + 625² делится на 6.
4. Разложите на множители способом группировки:
а) 3(а + с) + х(а + с); б) 6х – 6у + ах – ау;
Урок 6: Повторение. Системы двух линейных уравнений с двумя переменными.
1. Определение системы уравнений с двумя переменными
Напомним, что из себя представляет система двух линейных уравнений с двумя переменными. Это система вида:
Из первого уравнения 


Bторое линейное уравнение:



Запишем систему в другом виде:
Мы знаем, что множеством решений первого уравнения является множество точек, лежащих на соответствующей ему прямой, аналогично и для второго уравнения множество решений – это множество точек на другой прямой. Две прямые могут пересекаться – и тогда у системы будет единственное решение, единственная пара чисел х и у будет удовлетворять одновременно обоим уравнениям. Это происходит, если 




2. Способ подстановки
На данном уравнении можно продемонстрировать сразу несколько способов решения систем уравнений.
1 способ – способ подстановки: выразим во втором уравнении х и подставим полученное выражение в первое уравнение:
Подставим найденное значение у во второе уравнение и найдем значение х:
3. Способ алгебраического сложения
2 способ – способ алгебраического сложения: выполним сложение уравнений:
Из полученного уравнения найдем х:
Теперь вычтем из первого уравнения системы второе:
Таким образом, мы получили решение системы двумя способами, и это решение – точка с координатами (2; 1).
4. Системы уравнений с одним решением
В данном случае удобнее применить способ алгебраического сложения, вычтем из второго уравнения первое. Получаем:
Подставим значение у во второе уравнение и найдем х:
В данной системе нет переменных с одинаковыми коэффициентами, но мы можем их уравнять самостоятельно, для этого выполним преобразования:
Выполним сложение уравнений:
Подставим полученное значение у в первое уравнение и определим значение х:
5. Системы, имеющее бесконечное множество или не имеющие решений
Разделим второе уравнение на два:
Вычтем из первого уравнения второе:
Очевидно, что полученное выражение не зависит от значений переменных системы и не является верным числовым равенством, значит, система не имеет решений. В данном случае рекомендуется графически доказать, что система не имеет решений, для этого из уравнений записать линейные функции, построить их и показать, что прямые параллельны.
Очевидно, что, если разделить второе уравнение на два, получим первое уравнение:
Мы получили два одинаковых уравнения, значит, чтобы довести решение системы до конца, можем оставить одно: 

Графическая иллюстрация (рис. 1):
6. Подведение итогов урока
Вывод: мы рассмотрели системы двух линейных уравнений с двумя переменными, варианты и способы их решения. Мы вспомнили некоторые термины, понятия и свойства и решили примеры для закрепления техники.
1. Решите систему тремя способами: сложением, подстановки, графическим:
2. Сколько решений имеет система:
3. Решите систему любым способом:
Урок 7:Алгебраические дроби. Арифметические операции над алгебраическими дробями.Основные понятия.
На данном уроке рассматривается понятие алгебраической дроби. С дробями человек встречается в самых простых жизненных ситуациях: когда необходимо разделить некий объект на несколько частей, например, разрезать торт поровну на десять человек. Очевидно, что каждому достанется по 

1. Определение и примеры алгебраических дробей
Рациональные выражения делятся на целые и дробные выражения.
Определение.Рациональная дробь – дробное выражение вида 



Примерырациональных выражений: 



Значение алгебраической дроби, как и любого алгебраического выражения, зависит от численного значения тех переменных, которые в него входят. В частности, в первом примере значение дроби зависит от значений переменных 


Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.