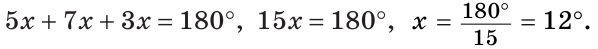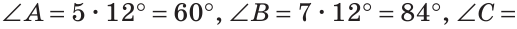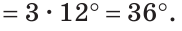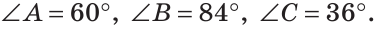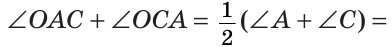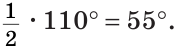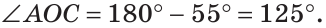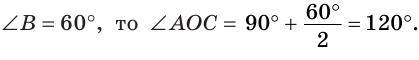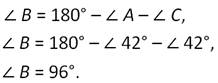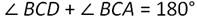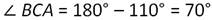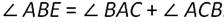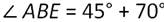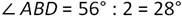Как доказать что сумма углов треугольника 180
Сумма углов треугольника
Сумма треугольника равна 180 градусов.
Это легко доказать. Нарисуйте треугольник. Через одну из его вершин проведите прямую, параллельную противоположной стороне, и найдите на рисунке равные углы. Сравните с решением в конце статьи.
А мы разберем задачи ЕГЭ, в которых фигурирует сумма углов треугольника.
1. Один из внешних углов треугольника равен 85 градусов. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85 градусов, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х. Получим уравнение
2. Один из углов равнобедренного треугольника равен 98 градусов. Найдите один из других его углов. Ответ дайте в градусах.
Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98 градусов?
Давайте отметим на чертеже еще несколько углов. Они нам понадобятся.
Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.
Ты нашел то, что искал? Поделись с друзьями!
Сумма углов треугольника:
Великий французский ученый XVII в. Блез Паскаль (1623—1662) еще в детстве любил изучать геометрические фигуры, открывать их свойства, измерять углы транспортиром.
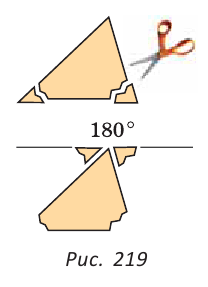
Юный исследователь заметил, что у любого треугольника сумма углов одна и та Ж6 180°. «Как же это объяснить?» — думал Паскаль. Тогда он отрезал у треугольника два уголка и приложил их к третьему (рис. 219). Получился развернутый угол, который, как известно, равен 180°. Это было его первое собственное открытие! Дальнейшая судьба мальчика была предопределена.
Теорема. Сумма углов треугольника равна 180°.
Дано: 
Доказать: 
Доказательство:
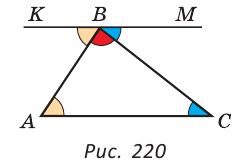
Через вершину В треугольника ABC проведем прямую КМ, параллельную стороне АС. Тогда 
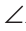
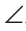





Следствия.
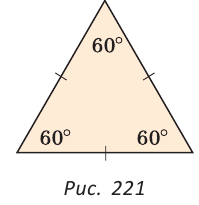
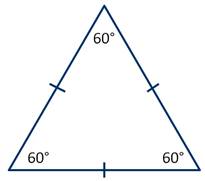
1. Каждый угол равностороннего треугольника равен 60°. (рис. 221).
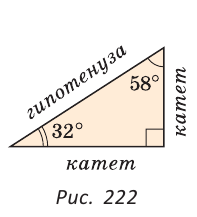
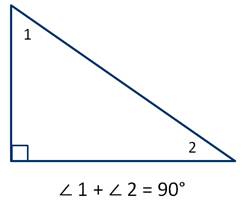
2. Сумма острых углов прямоугольного треугольника равна 90° (рис. 222).
В прямоугольном треугольнике стороны, заключающие прямой угол, называются катетами, сторона, противолежащая прямому углу, — гипотенузой (см. рис. 222).
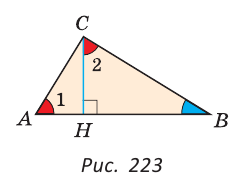
Проведем в прямоугольном треугольнике ABC высоту СН к гипотенузе АВ (рис. 223). Так как в треугольнике ABC угол 1 дополняет угол В до 90°, а в треугольнике СНВ угол 2 также дополняет угол В до 90°, то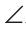
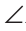
Доказано свойство: «Угол между высотой прямоугольного треугольника, проведенной к гипотенузе, и катетом равен углу между другим катетом и гипотенузой».
Пример:
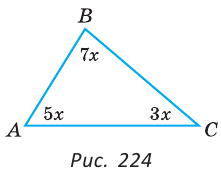
В треугольнике ABC градусные меры углов А, В и С относятся соответственно как 5:7:3. Найти углы треугольника (рис. 224).
Решение:
Пусть 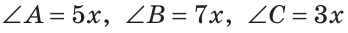
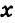
Так как сумма углов треугольника равна 180°, то
Тогда
Ответ:
Пример:
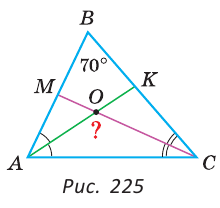
В треугольнике ABC (рис. 225) угол В равен 70°, АК и СМ — биссектрисы, О — точка их пересечения. Найти угол АОС между биссектрисами.
Решение:
Из треугольника АОС находим:
Замечание. Если 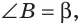
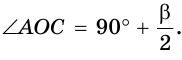
Пример:
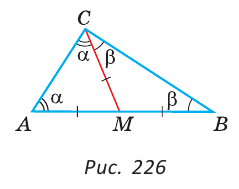
Доказать, что если медиана треугольника равна половине стороны, к которой она проведена, то данный треугольник — прямоугольный.
Доказательство:
Пусть СМ — медиана, 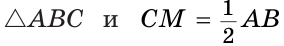
Докажем, что























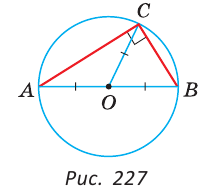
Замечание. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным. На рисунке 227 это угол АСВ. Из задачи 3 следует свойство: «Вписанный угол, опирающийся на диаметр, — прямой».
Пример:
Доказать, что в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Доказательство:
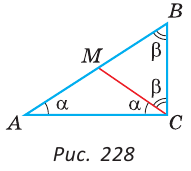
Пусть в треугольнике ABC (рис. 228) 




Проведем отрезок СМ так, что










При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Теорема о сумме углов треугольника
Урок 19. Геометрия 7 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Теорема о сумме углов треугольника»
Блез Паскаль, великий французский учёный 17-го века, заметил, что у всех треугольников сумма 3-х углов равна 180 градусов. И у него возник вопрос: «Как это доказать?»
И он отрезал ножницами два уголка треугольника и приложил их к третьему углу. В результате получился развёрнутый угол, градусная мера которого, как вам уже известно, равна 180 градусов.
Сумма углов треугольника равна 180 градусов.
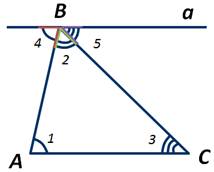
Проведём прямую а через точку В параллельно стороне АС.
Сумма градусных мер ∠4, ∠2 и ∠5 равна градусной мере развёрнутого угла с вершиной в точке В, то есть ∠4+∠2+∠5=180 градусов.
А так как ∠1=∠4, ∠3=∠5, то получаем, что ∠1+∠2+∠3=180 градусов. То есть ∠А+∠В+∠С=180 градусов. Теорема доказана.
Из теоремы следует:
1. Углы равностороннего треугольника равны по 60 градусов.
2. Сумма острых углов прямоугольного треугольника равна 90 градусов.
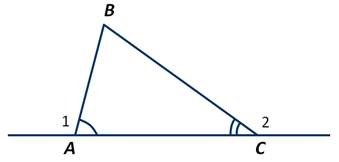
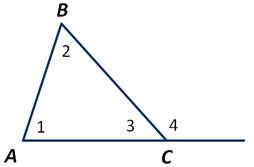
Внешним углом треугольника называют угол, смежный с каким-либо углом треугольника.
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
Сумма градусных углов 3 и 4 равна градусной мере развёрнутого угла, то есть ∠3+∠4=180 градусов. А по теореме о сумме градусных мер углов треугольника ∠1+∠2+∠3=180 градусов. Из полученных двух равенств следует, что ∠1+∠2=∠4. Что и требовалось доказать.
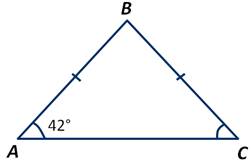
Стороны АВ и ВС треугольника АВС равны. ∠А=42 градуса. Чему равна градусная мера угла В?
Так как АВ=ВС, то треугольник АВС является равнобедренным. Нам известно, что углы при основании равнобедренного треугольника равны. А значит, ∠С=42 градуса.
По теореме о сумме углов треугольника ∠А+∠В+∠С=180 градусов. Из этого равенства получаем:
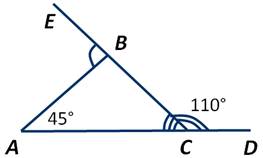
На рисунке ∠ВСD=110 градусов, а ∠ВАС=45 градусов. Найти градусную меру ∠АВЕ.
Искомый ∠АВЕ является внешним углом нашего треугольника, смежным с ∠АВС. А значит:
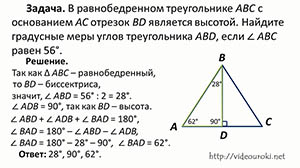
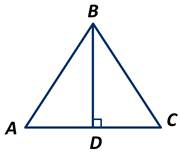
В равнобедренном треугольнике АВС с основанием АС отрезок ВD является высотой. Найдите градусные меры углов треугольника ABD, если ∠АВС=56 градусов.
По теореме о сумме углов треугольника, получаем: